LFMCW雷达解速度模糊和近场校正方案
LFMCW雷达解速度模糊和近场校正方案
解速度模糊
对于LFMCW雷达,采用一种简单的解速度模糊技术. 它可以将目标的不模糊速度提高到 2 v m a x 2v_{max} 2vmax, 甚至允许对大于 2 v m a x 2v_{max} 2vmax的目标速度进行X/Y坐标的纠正计算. 该技术需要在CFAR检测阶段之后执行以下步骤. 对于每一个被检测到的目标, 假设对虚拟天线的多普勒纠正已经完成:
- 将已经进行过多普勒纠正的天线数据A复制到azimuthIn的较高地址区域(下图中标记为B).执行这一步是因为DSPlib FFT 函数会用保留的索引(index)重写输入缓冲区, 而我们需要稍后对执行过符号翻转的Tx2数据计算FFT.
- 计算azimuth FFT (在A区域),然后计算FFT输出的幅度平方.
- 保存结果azimuthMagSqr 到集合(set)0,"uncorrected set",(参考下图).
- 将区域B中对应Tx2天线的数据翻转符号.把区域B的数据复制到区域A,并补零.
- 重复步骤4.
- 保存结果azimuthMagSqr 到集合(set)1, “corrected set”.
- 在每个集合中搜索最大值, 然后选择最大值出现的那个集合.
- 如果最大值出现在"corrected set", 将估计的速度纠正为:
v c o r r = v e s t + 2 v m a x ( i f v s e t < 0 ) v c o r r = v e s t − 2 v m a x ( i f v s e t > 0 ) v_{corr}=v_{est}+2v_{max}(if\ v_{set}<0) \\ v_{corr}=v_{est}-2v_{max}(if\ v_{set}>0) vcorr=vest+2vmax(if vset<0)vcorr=vest−2vmax(if vset>0)
否则, 不需要进行纠正. - 使用选中集合的索引 i m a x i_{max} imax计算X/Y坐标.
下图是扩展最大速度操作的数据通路(data path):

下图采用一个例子展示了这个技术, 该例子中包含了两种情况,情况一(Case a): 一个运动目标以小于 V m a x V_{max} Vmax的速度在相对雷达正的角度远离雷达,情况二(Case b):相同情况目标运动速度大于 V m a x V_{max} Vmax. 下图展示了用于3个连续chirp的2D - FFT 天线符号: n, n+1, n+2 ( 蓝, 绿, 红). Chirp n和n+1的符号用于角度FFT计算. 多普勒频移, 相位 ψ t r u e \psi_{true} ψtrue位于chirp n和n+2之间, (同一发射天线的连续chirp), 通过2D-FFT结果被估计为 ψ e s t \psi_{est} ψest. 对于情况一, ψ t r u e < π \psi_{true}<\pi ψtrue<π, 并且 ψ e s t ≈ ψ t r u e \psi_{est}\approx \psi_{true} ψest≈ψtrue. 对于情况二, ψ t r u e > π \psi_{true}>\pi ψtrue>π, (多普勒速度出现模糊), 而且 ψ e s t \psi_{est} ψest被估计为一个负值,(目标正在接近雷达). 多普勒补偿首先将chirp n+1旋转 − ψ e s t / 2 -\psi_{est}/2 −ψest/2从而使它和第n个chirp的符号对齐,然后对这些数据计算角度FFT,并将输出存放到集合0. 然后翻转第n+1个chirp的符号,然后再对他们执行角度FFT并将结果存入集合1.在情况一中, V < V m a x V
近场校正
问题介绍和算法描述

在角度估计中,我们假设目标位于远场,因此目标和多个TX/RX天线之间的电磁波是平行的. 然而对于目标距离非常近的情况(参考上图), 该假设(平行波)将不再有效, 并且当使用传统的FFT技术时, 将会造成一个明显的相位误差:
- 路径Tx1©->object(O)->Rx4(D) (红线)和Tx2(A)->object(O)->Rx1(E) (绿线)之间的相位误差最为明显. 这对应于虚拟天线4和5之间的相位差.
- 相位误差随着目标距离的增加而减小
- 对于一个固定的距离, 位于雷达中心视轴上的目标相位误差最严重,随着角度的偏移; 相位误差逐渐减小.当目标所在角度与雷达视轴呈90度时, 相位误差为0;
该相位误差会导致在角度FFT上出现一个虚假峰值, 从而会在使能多目标的波束合成时形成一个虚假目标. 为了减小这种误差的影响,在物理天线和虚拟天线之间的相位相位误差需要被纠正. 这要基于检测到目标的几何角度和距离. 具体操作方式如下:
根据8根虚拟天线, 我们令x为一个 1 × 8 1\times8 1×8向量.令F表示对x的64点FFT; 例如F=fftshift(fft(x,64)); 类似的, 令 F 1 F_1 F1和 F 2 F_2 F2分别表示x(1:4)和x(5:8)的64点FFT. 然后, 有如下等式:
F ( k ) = F 1 ( k ) + F 2 ( k ) e − j 2 π k 4 / 64 ; − 32 ≤ k ≤ 31 ; F(k)=F_1(k)+F_2(k)e^{-j2{\pi}k4/64};-32{\le}k{\le}31; F(k)=F1(k)+F2(k)e−j2πk4/64;−32≤k≤31;
上式可以被修改为
F ( k ) = F 1 ( k ) + F 2 ( k ) e − j 2 π k 4 / 64 e − j ϕ ( k , r ) ; − 32 ≤ k ≤ 31 ; F(k)=F_1(k)+F_2(k)e^{-j2{\pi}k4/64}e^{-j\phi(k,r)};-32{\le}k{\le}31; F(k)=F1(k)+F2(k)e−j2πk4/64e−jϕ(k,r);−32≤k≤31;
这里的 ϕ ( k , r ) \phi(k,r) ϕ(k,r)是由角度k和距离r决定的近场相位误差. 它可以先通过上图中的几何关系进行计算:
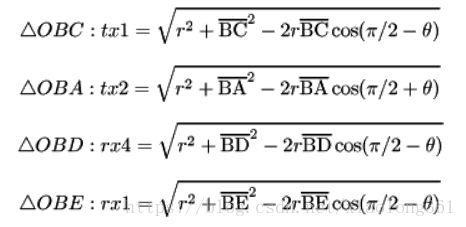
带入 θ = a r c s i n ( 2 k / 64 ) \theta=arcsin(2k/64) θ=arcsin(2k/64), 上式可以简化为:

注意: B C ‾ \overline{BC} BC, B A ‾ \overline{BA} BA, B D ‾ \overline{BD} BD, B E ‾ \overline{BE} BE都是常数, 因此上面的计算包括4*(3个乘法 + 2个加法/减法 + 平方根).
正如Data Path - (X,Y) Estimation中提到的那样, 在远场情况下连续天线之间的相位差是 w x = π s i n ( θ ) w_x={\pi}sin(\theta) wx=πsin(θ). 因此相位可以通过下式计算:

执行细节

参考上图, 对于每个检测到的点, 假设虚拟天线的多普勒校正已经完成:
- 将Tx2相应的天线数据复制到azimuthIn的较高地址区域(上图中标记为B).并在A(Tx1的天线数据)和B之间填充0. 执行这一步的目的是为了保留Tx2数据用于下一次计算.计算azimuthIn中的前64采样点FFT并将其存储到azimuthOut中的较低地址空间(图中的set 0).这是 F 1 ( k ) F_1(k) F1(k).
- 将存储在较高地址区域中的Tx2数据复制回之前的位置.对前4个天线(对应Tx1)和B之后的数据位置全部补0.计算azimuthIn中前64采样点的FFT,并保存到azimuthOut中的较高地址空间(图中的set 1).这就是 F 2 ( k ) e − j 2 π k 4 / 64 F_2(k)e^{-j2{\pi}k4/64} F2(k)e−j2πk4/64.
- 在set 1对所有 k ∈ [ − 32 , 31 ) k\in[-32,31) k∈[−32,31)应用校正因子e^{-j\phi(k,r)}然后和set 0相加,求和的结果可以放到比如set 0的位置.
- 执行角度计算的其他步骤(幅度平方等)
注意:
- 由校正过程带来的距离估计误差可以通过在计算相位校正之前就得到距离来消除.估计相位误差的函数是MmwDemo_nearFieldCorrection.
- 目前解速度模糊没有用到近场校正,因为执行复杂度较高,而且在近场环境下一般出现高速目标的可能性较小.
用户接口
提供了一个带参数的CLI命令"nearFieldCfg"来启动/禁用近场校正, 并且可以指定触发该工程的距离维索引范围. 相位误差在雷达中心视轴( θ = 0 \theta=0 θ=0)最大.下面的数据均是在雷达中心视轴上获得,他们通过问题介绍和算法描述一节中的公式计算得到, 可以用来作为决定需要启动近场校正的最大距离范围的一个参考.
| Distance (cm) | Phase Error (degrees) |
|---|---|
| 5 | 177.8 |
| 10 | 90.3 |
| 20 | 45.3 |
| 40 | 22.7 |
| 80 | 11.4 |
| 100 | 9.1 |
| 200 | 4.5 |
| 400 | 2.3 |
| 1000 | 0.9 |
注意:
- 距离维索引没有排除距离偏差.例如,如果距离偏移是6cm, 而距离步长(每个距离门对应的长度)为2cm, 那么距离雷达4cm时将会是(6+4)/2,即5个距离门,即距离维索引为4.
- 由于近场校正在近场条件下对每个目标点都要进行若干计算(主要是64*(4 square root + 1 sin + 1 cosine)),因此DSP将会为之消耗一些MIPS.目前对于在近场范围内使能近场校正的情况,每个目标点需要消耗大约35000个指令周期,这对于600MHz的DSP来说,大约是58us.
- 由于不明原因, 该方法无法在5cm以内的范围内可靠运行,因此建议对于在范围以内禁用近场校正(使用配置推荐的距离起始索引参数即可).
- 近场校正没有用到目标输出的角度-距离 HeatMap数据上.
