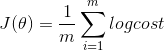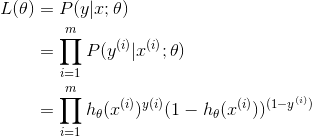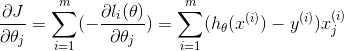手写逻辑回归 ——Logistic Regression的详细推导与python实现
Logistic Regression是一种分类算法,返回分类0或者1
逻辑回归将样本线性分割为两类,跟样本距离分割线的距离和正负来推算样本可能的类别
产生的分割线,也叫 决策边界,Decision Boundary为
![]()
样本到分割线的距离为
![]()
则预测函数为
![]()
对于二分类问题,代价的分布可以认为是伯努利分布,则根据极大似然估计法可以推得其中g一般为S型函数 sigmoid function 或者 logistic function
把这个函数画出来
def __sigmoid(z):
epart = np.exp( z )
return epart / (1 + epart)
z = np.arange(-20,20)
plt.plot(z, __sigmoid(z))
plt.title('sigmoid')
plt.show()所以总的预测函数hyperthesis为
#for n feature, x = 0:n, theta = 0:n
def __hypothetic(self, x):
z = np.dot(self.theta, x) + self.intercept
return self.__sigmoid(z)这样h将返回给定x, y=1的概率,即
![]()
通过添加多项式回归参数,比如 x1, x1^2, x2, x2^2等等,线性逻辑回归也可以分类非线性问题。
单个代价为
![]()
取Log, 最大化L既可以得到theta
![]()
#y log h + (1 - y) log( 1- h )
def __loglikelihood(self, x, y):
h = self.__hypothetic(x)
return y * np.log(h) + (1 - y)*np.log(1 - h)这是,代价函数
#J = - mean of likelihood
def __Jfunction(self):
sum = 0
for i in range(0, self.m):
sum += self.__loglikelihood(self.x[i], self.y[i])
return 1/self.m * sum可以用梯度下降 gradient descent 来求解 J的最小值
其中
#mean of ( h - y ) * x_j = [dist matrix for sample] dot sample
def __partialderiv_J_func(self,):
h = np.zeros(self.m)
for i in range(0, self.m):
h[i] = self.__hypothetic(self.x[i])
dist = h - self.y
return np.asarray(np.mat(dist.T) * self.x) / self.m
#\frac{1}{m}\sum X^T(\theta_TX-y)
def __partialderiv_J_func_for_intersect(self):
sum = 0
for i in range(0, self.m):
err = self.__error_dist(self.x[i], self.y[i])
sum += err
return 1/self.m * sum梯度下降的代码
#\theta = \theta - \alpha * \partial costfunction
def __gradient_descent(self):
cost = 100000.0
last_cost = 200000.0
threshold = 0.01
self.iter_count = 0
#repeat until convergence
while abs(cost - last_cost) > 0.0001:
last_cost = cost
self.theta = self.theta - self.alpha * self.__partialderiv_J_func()
self.intercept = self.intercept - self.alpha * self.__partialderiv_J_func_for_intersect()
cost = -self.__Jfunction()
self.cost_history.append(cost)
print('iter=%d deltaCost=%f'%(self.iter_count, last_cost - cost))
self.iter_count += 1除了梯度下降,还可以采用
Conjugate gradient
BFGS
L-BFGS来算
或者牛顿法,用二次梯度来算也很快
那么逻辑回归的代价函数是怎么得来的呢?
我们通过极大似然估计来推导逻辑回归的代价函数。
因为对某个正例样本,即y(i)=1的情况,预测x(i)属于该样本的概率就是H函数,即
![]()
对负例样本有
![]()
那么统一成一个式子可以得到y的分布
![]()
对单个样本是这样,那么对所有样本,可以得到似然函数为
取对数可以得到
最大化![]() 就是最小化
就是最小化![]() 也就是我们的logcost函数
也就是我们的logcost函数
我们对l 求导,先对l_i(theta)求导然后再加起来即可
首先将l_i(theta)变换一下方便求导
将h展开
有
带入l_i(\theta)
![]()
求导
因为我们的J函数其实是-l_i(theta)
所以
最后结果如下图,红色线为sklearn计算的结果,绿色线为我们手写算法计算的结果
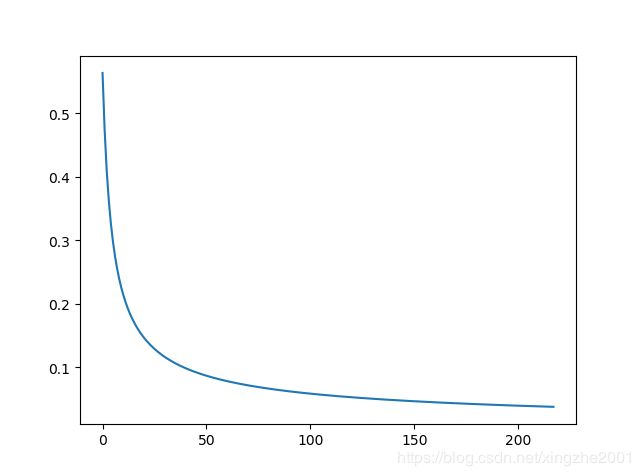
代价函数随着迭代次数下降的图为
完整代码在这里
#一个手写的逻辑回归
import numpy as np
class LogisticRegression:
def __init__(self, normalize = True, alpha=0.3):
self.coef_ = 0.0
self.intercept = 0.
self.theta = None
self.normalize = normalize
self.offset = 1.0
self.scalar = 1.0
self.alpha = alpha
self.iter_count = 0
self.cost_history=[]
pass
# e/(1+e^ax)
def __sigmoid(self, z):
epart = np.exp( z )
return epart / (1 + epart)
#for n feature, x = 0:n, theta = 0:n
def __hypothetic(self, x):
z = np.dot(self.theta, x) + self.intercept
return self.__sigmoid(z)
#distance for single sample or all the samples
def __error_dist(self, x, y):
return self.__hypothetic(x) - y
#y log h + (1 - y) log( 1- h )
def __loglikelihood(self, x, y):
h = self.__hypothetic(x)
return y * np.log(h) + (1 - y)*np.log(1 - h)
#J = - mean of likelihood
def __Jfunction(self):
sum = 0
for i in range(0, self.m):
sum += self.__loglikelihood(self.x[i], self.y[i])
return 1/self.m * sum
#mean of ( h - y ) * x_j = [dist matrix for sample] dot sample
def __partialderiv_J_func(self,):
h = np.zeros(self.m)
for i in range(0, self.m):
h[i] = self.__hypothetic(self.x[i])
dist = h - self.y
return np.asarray(np.mat(dist.T) * self.x) / self.m
#\frac{1}{m}\sum X^T(\theta_TX-y)
def __partialderiv_J_func_for_intersect(self):
sum = 0
for i in range(0, self.m):
err = self.__error_dist(self.x[i], self.y[i])
sum += err
return 1/self.m * sum
#\theta = \theta - \alpha * \partial costfunction
def __gradient_descent(self):
cost = 100000.0
last_cost = 200000.0
threshold = 0.01
self.iter_count = 0
#repeat until convergence
while abs(cost - last_cost) > 0.0001:
last_cost = cost
self.theta = self.theta - self.alpha * self.__partialderiv_J_func()
self.intercept = self.intercept - self.alpha * self.__partialderiv_J_func_for_intersect()
cost = -self.__Jfunction()
self.cost_history.append(cost)
print('iter=%d deltaCost=%f'%(self.iter_count, last_cost - cost))
self.iter_count += 1
def __calculate_norm_params(self, x):
offset = np.zeros(self.n_feature)
scalar = np.ones(self.n_feature)
for feature_idx in range(0, self.n_feature):
col = x[:, np.newaxis, feature_idx]
min = col.min()
max = col.max()
mean = col.mean()
if( min != max):
scalar[feature_idx] = 1.0/(max - min)
else:
scalar[feature_idx] = 1.0/max
offset[feature_idx] = mean
return offset, scalar
def __normalize(self, x):
return (x - self.offset) * self.scalar
def fit(self, x, y):
if x.shape[0] != y.shape[0]:
raise 'x, y have different length!'
self.m = x.shape[0]
self.n_feature = x.shape[1]
self.theta = np.zeros(x[0].size)
if self.normalize:
self.offset, self.scalar = self.__calculate_norm_params(x)
self.x = self.__normalize(x)
else:
self.x = x
self.y = y
self.__gradient_descent()
self.coef_ = self.theta
pass
def predict(self, x):
y_pred = []
for element in x:
xi = element
if self.normalize:
xi = self.__normalize(element)
y_pred.append(self.__hypothetic(xi))
return y_pred