数据结构与算法系列第三篇——树(红黑树)
红黑树
- 二叉搜索树引入的问题
- 平衡树和非平衡树
- 非平衡树的补救措施
- 红黑树
- 红黑树的修正措施
- 红黑规则和平衡树
- 空子节点
- 旋转
- 简单旋转
- 横向移动节点
- 移动子树
- 红黑树插入一个新节点
- 在下行路途中的颜色变换
- 插入节点之后的旋转
- 可能性1:P是黑色的
- 可能性2:P是红色的,X是G的一个外侧子孙节点
- 可能性3:P是红色的,X是G的一个内侧子孙节点
- 在下行路途中的旋转
- 外侧子孙节点
- 内侧子孙节点
- 结论
- 删除
- 红黑树的效率
- 其他平衡树
- 小结
二叉搜索树引入的问题
如果树中插入的是随机数据,则执行效果很好。但是,如果插入的是有序的数据的数据,速度就会变得特别慢。**因为当插入的数值有序时,二叉搜索树就退化成了链表的形式了。**此时,也可以说这棵树是非平衡树,那么它的快速查找(插入,删除)指定数据项的能力就丧失了。
如下图所示:
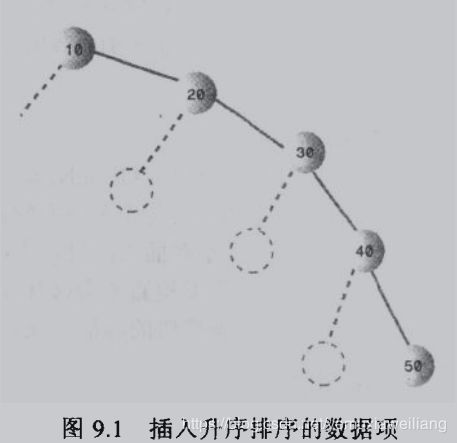
平衡树和非平衡树
平衡树,即平衡二叉树(Balanced Binary Tree),具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
图9-1是一种极端不平衡的树,它的事件复杂度为O(N)。所以搜索部分非平衡树的时间介于O(N)和O(logN)之间,这取决于树的不平衡程序。
非平衡树的补救措施
在插入过程中,对于一个要插入的数据项,插入例程要检查不会破坏树一定的特征。如果破坏了,程序就会进行纠正,根据需要更改树的结构。通过维持树的特征,保证了树的平衡。我们将这种方式成为旋转。
红黑树
红黑树是一种自平衡的二叉搜索树
它的规则如下:
- 1.每一个节点不是红色就是黑色
- 2.根总是黑色的
- 3.如果节点是红色的,则它的子节点必须是黑色的
- 4.从根到叶节点或空子节点的每条路径,必须包含相同数量的黑色节点。
红黑树的修正措施
- 改变节点的颜色
- 执行旋转操作
红黑规则和平衡树
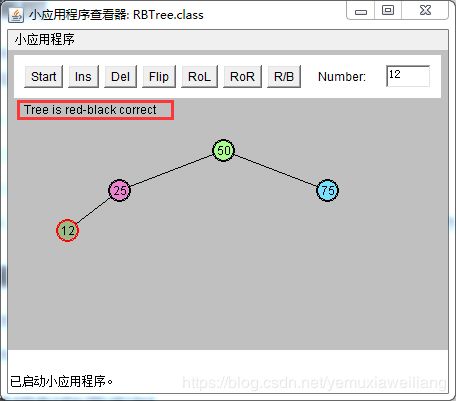
为什么红黑规则能保证树是平衡的?
如果一条路径上的节点数比另一条路径上的节点数多一个以上(不包含1个),那它要么有更多的黑色节点,违背了规则4。要么有两个相邻接的红色节点,违背了规则3。
空子节点
如果节点只有右子节点,那么它的空缺的左子节点就是空子节点。反之亦然。
如下图所示:

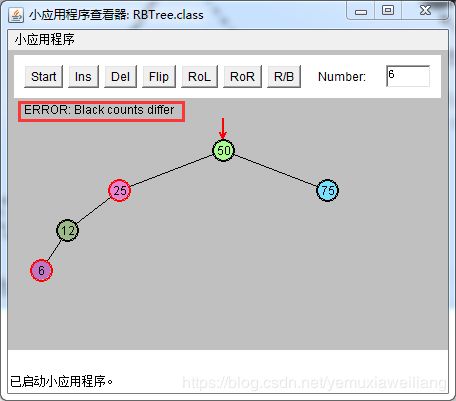
旋转
旋转要做的两件事情:
- 使一些节点上升,一些节点下降,帮助树平衡
- 保证不破坏二叉搜索树的特征
简单旋转
向左旋转或者向右旋转
选择一个节点作为旋转的“顶端”。如果做一次右旋,这个“顶端”节点将会向下和向右移动到它右子节点的位置。它的左子节点将会上移到它原来的位置。
注意事项:
如果做右旋,顶端节点必须有一个左子节点。否则,将没有节点旋转到顶端节点原来所在的位置。类似,左旋,顶端节点必须有一个右子节点。
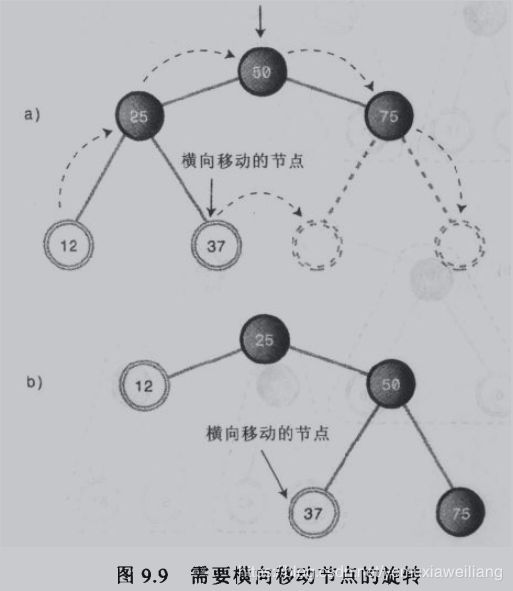
横向移动节点
移动子树
- 顶端节点(50)移动到它右子节点的位置
- 顶端节点的左子节点(25)移动到顶端的位置上
- 以节点12为根的整棵子树都向上移动
- 以节点37为根的整棵子树横向移动,成为节点50的左子节点
- 以节点75为根的整棵子树都向下移动
红黑树插入一个新节点
需要解决以下三个问题:
- 在下行路途中的颜色变换
- 插入节点之后的旋转
- 在向下路途中的旋转。
在下行路途中的颜色变换
红黑树的插入例程的开始时所做的事情和普通的二叉搜索树所做的基本一样:沿着根朝插入点位置走,在每一个节点处通过比较节点的关键字相对大小来决定向左走还是向右走。
查找插入新节点的位置,为了不违反颜色规则,在必要的时候需要进行颜色变换。
规则:每当查找例程遇到一个有两个红色子节点的黑色节点时,它必须把子节点变为黑色,而把父节点变为红色(除非父节点为根节点,根总是黑色的)
如下图所示:
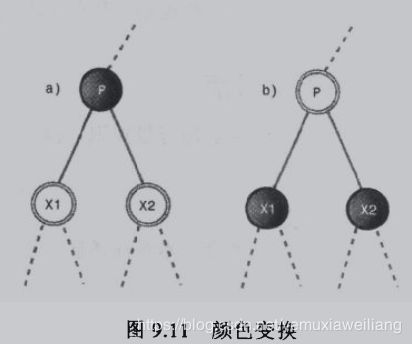
这种颜色变换之后带来的好处:
- 黑色高度不改变
- 对根的两个子节点做颜色变换,根和它的两个子节点一样都是黑色的。这样不违背规则2,3,4
这种颜色变换之后也带来了新问题:
如果P的父是黑色的,则P由黑色变成红色不会有问题。但是,如果P的父节点是红色的,那么,在P的颜色变化之后,就有两个红色节点相连接了,违背了规则3.
插入节点之后的旋转
新数据项的插入可能会违背红黑规则,因此,在插入之后,必须要检测是否违背规则,并采用相应的措施。
如下图所示,有四种情况
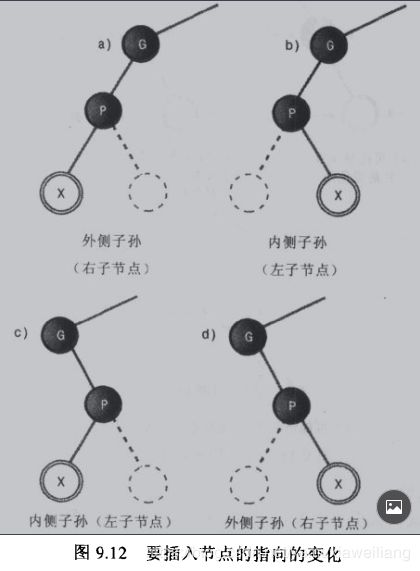
如果节点X在P的一侧与P在G的一侧相同,则X就是一个外侧子孙节点。相反,如果节点X在P的一侧,而P在G的另一侧,则X就是一个内侧子孙节点。
有了上述概念之后,四种情况归纳为三种:
新插入的X总是红色的
- 1.P是黑色的
- 2.P是红色的,X是G的一个外侧子孙节点
- 3.P是红色的,X是G的一个内侧子孙节点
可能性1:P是黑色的
如果P是黑色,什么事情也不用做。因为刚刚插入的节点总是红色的。如果它的父节点是黑色,则没有红色节点连接红色节点的冲突(规则3)。并且也不会增加黑色节点的数目(规则4)。因此,不需要做其他事情,插入完成。
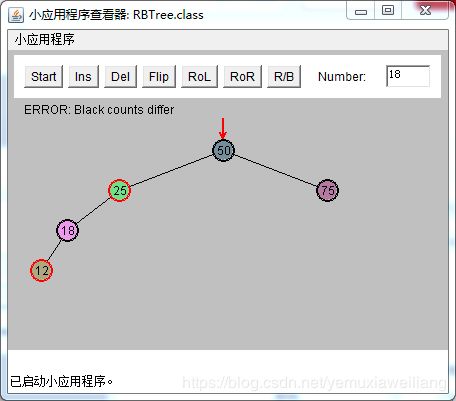
可能性2:P是红色的,X是G的一个外侧子孙节点
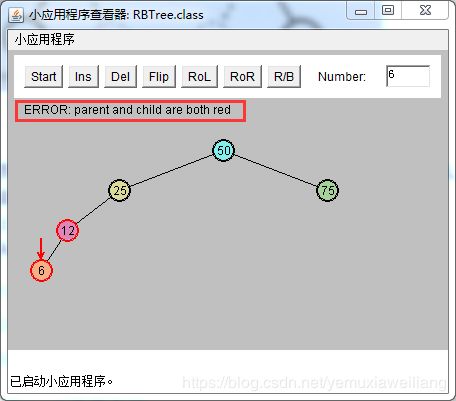
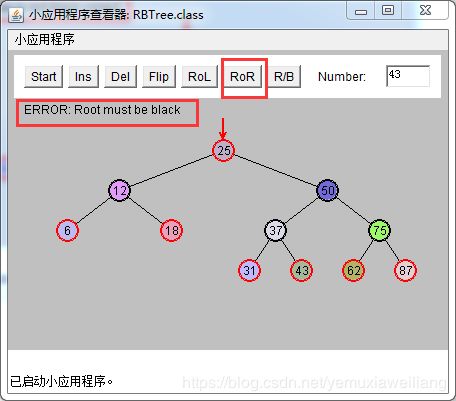
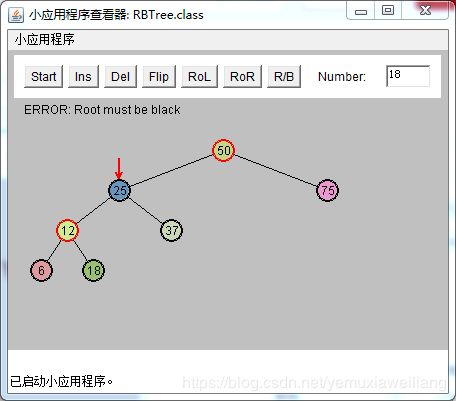
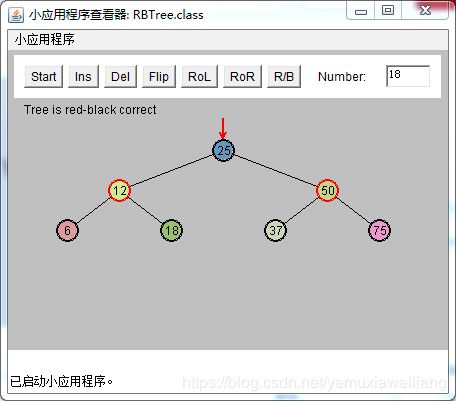
改变X的祖父节点G(25)的颜色
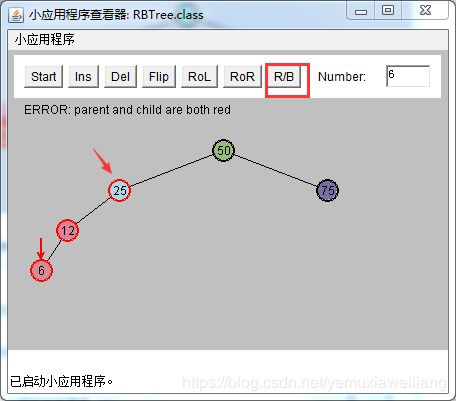
改变X的父节点P(12)的颜色

以X的祖父节点G(25)为顶旋转,向X(6)上升的方向。做一次右旋操作
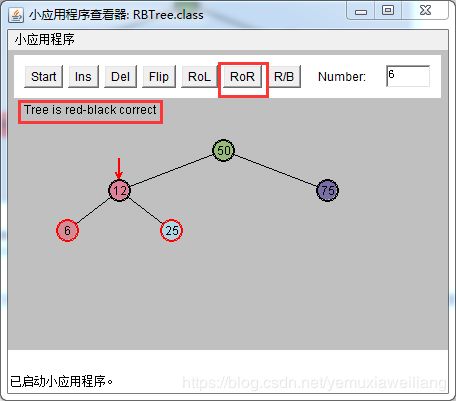
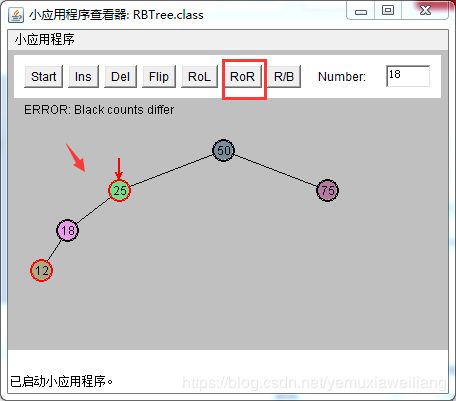
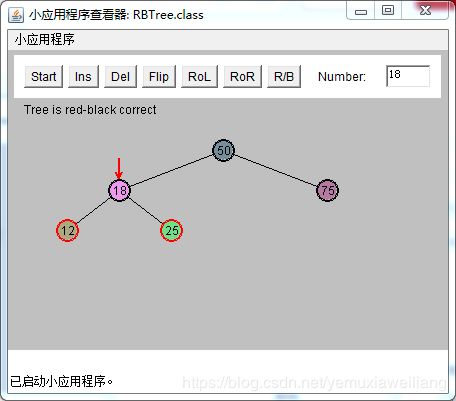
可能性3:P是红色的,X是G的一个内侧子孙节点
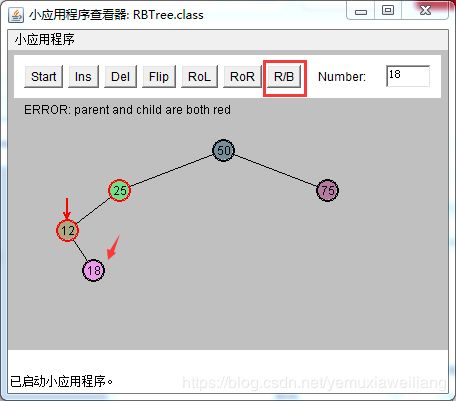
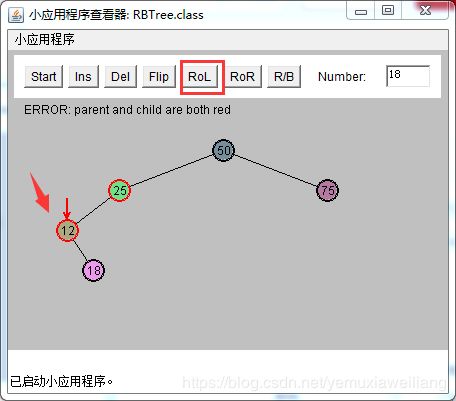
如下图所示:
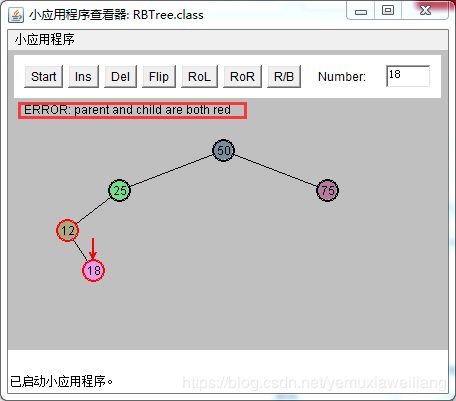
当X(18)是内侧子孙节点时,其解决技巧是执行两次旋转。第一次把X由内侧子孙节点变为外侧子孙节点。再按照 外侧子孙节点的情况进行处理。
操作步骤如下(一般是先着色,再旋转):
在下行路途中的旋转
在下行路途中查找插入点时所做的旋转
在向下的路径上有两种旋转的可能性,分别对应前面描述的在插入阶段的可能性2和可能性3。违背规则的节点可能是一个外侧子孙节点,也可能是一个内侧子孙节点。
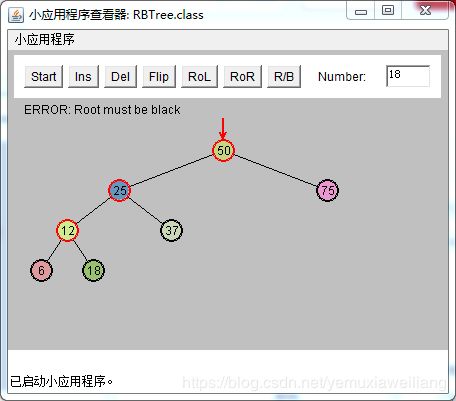
外侧子孙节点
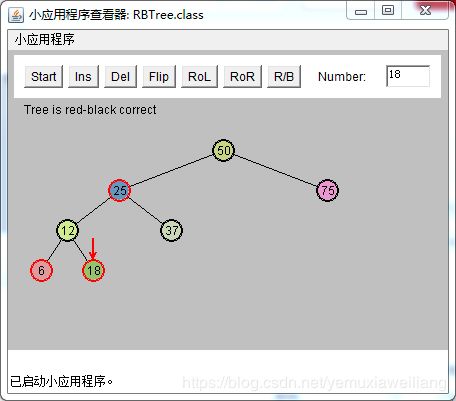
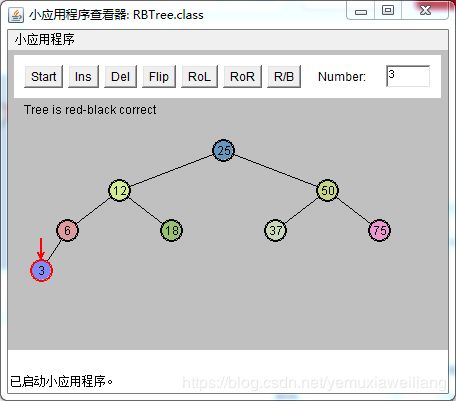
注意:在插入12和6时已经做了两次颜色变换,否则不能插入新节点
现在要插入值为3的节点。必须对节点12以及它的子节点6和18做颜色变换。
变换后如下图:
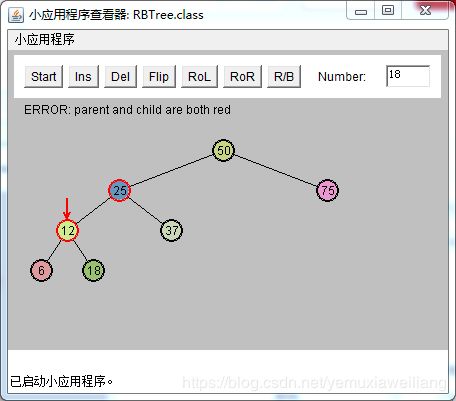
纠正这种违规情况和前面讨论的插入的可能情况2类似。必须要执行两次颜色变换和一次旋转。
以刚刚做了颜色变换三角形的顶端节点为X(12),P(25),G(50)
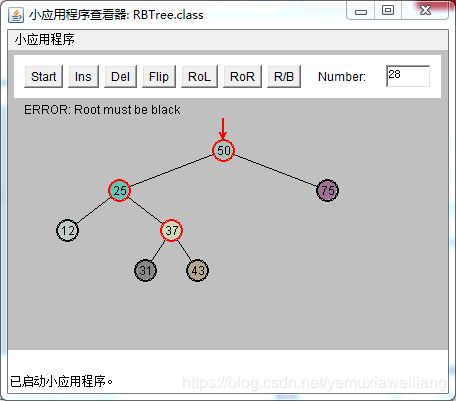
内侧子孙节点
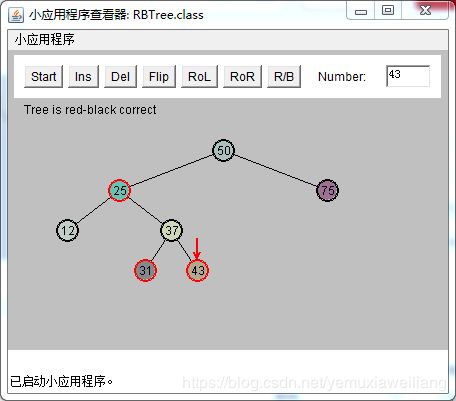
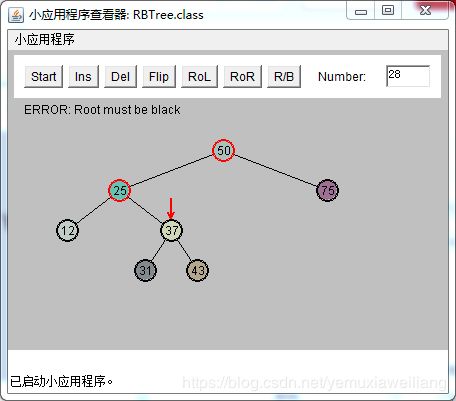
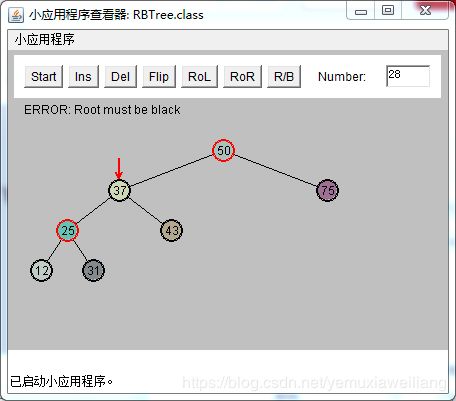
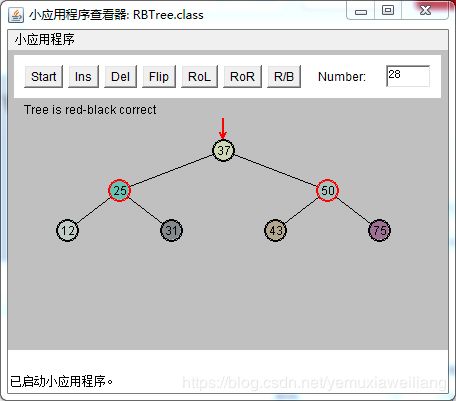
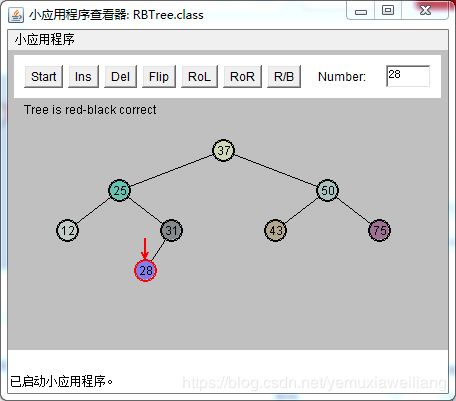
插入一个新节点28,需要颜色变换。此时25和37都是红色。G(50),P(25),X(37)
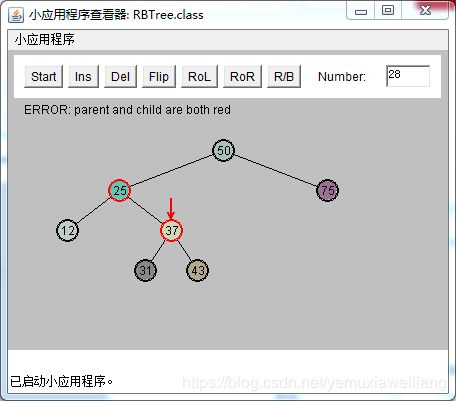
为了解决红-红冲突。需要做和可能性3相同的两次颜色变换和两次旋转。
结论
在插入的过程中,保证树的红黑特性,可以取得树的平衡
删除
在普通二叉搜索树中编写删除操作的代码比编写插入操作要难得多。在红黑树也是这样的,并且在删除过程由于需要在节点删除之后恢复树的红黑正确性,变得更复杂。
由于删除的复杂性,在实际操作中都是规避真正的删除节点。就是为删除的节点做个标记而不实际的删除它。任何找到该节点的查找例程都知道不用报告已找到该节点
红黑树的效率
红黑树的查找,插入和删除的时间复杂度为O(logN)。在红黑树的查找时间和在普通的二叉搜索树查找时间几乎一样,因为在查找的过程中并没有应用到红黑树的特征,额外的开销只是每一个节点的存储空间都稍微增加了一点,来存储红黑树的颜色(boolean变量)。
插入和删除的时间要增加一个常数因子,因为不得不在下行的路径上和插入点执行颜色变换和旋转。平均起来,一次插入大约需要一次旋转。因此,插入的时间复杂度还是O(logN),但是比普通的二叉搜索树要慢。
大多数应用中,查找的数次比插入和删除的次数多,所以使用红黑树取代普通的二叉搜索树总体不会增加太多的时间开销。
红黑树的优点是对有序数据的操作不会慢到O(N)的时间复杂度
其他平衡树
AVL树:在AVL树中,每个节点存储一个额外的数据,它的左子树和右子树的高度差,这个差值不会大于1.也就是说,节点的左子树的高度和右子树的高度相差不会大于1层。
插入之后,检查新节点的插入点所在的最低子树的根。如果它的子节点的高度相差大于1,执行一次或者两次旋转使它们的高度相同。然后算法上移,检查上面的节点,必要时均衡高度。这个检测检查所有路径一直向上,直到根为止。
AVL树查找的时间复杂度为O(logN),因为树一定是平衡的。但是,由于插入(删除)一个节点需要扫描两趟树,一次向下查找插入点,一次向上平衡树,所以:
AVL树不如红黑树效率高,也不如红黑树常用。
小结
- 保持二叉搜索树的平衡是为了查找给定节点所需要的时间尽可能的短
- 插入有序的数据将创建最不平衡的树,它的查找时间复杂度为O(N)
- 在红黑平衡的方法中,每个节点的颜色不是红的就是黑的
- 红黑树的4大规则(背诵并理解)
- 节点不是红的就是黑的
- 根节点必须为黑色
- 红色节点的子节点一定为黑色
- 从根到各个叶子节点(空子节点)的黑色节点的数目是相等的
- 插入或者删除一个节点时应用这些规则
- 一次颜色变换把一个黑色节点和它的两个红色子节点改为一个红色节点和两个黑色子节点
- 在一次旋转中,指定一个节点为顶端节点
- 右旋把顶端节点移动到它的右子节点的位置,并把顶端节点的左子节点移动到顶端节点的位置
- 左旋是把顶端节点移动到它的左子节点的位置,并把顶端节点的右子节点移动到顶端节点的 位置
- 当顺着树向下查找新节点的插入位置时,应用颜色变换,并且有时应用旋转。颜色变换通过简单的方法,就使树在插入后恢复成正确的红黑树
- 新节点插入后,检查红红冲突。如果发现违背红黑规则现象,执行适当的旋转使树恢复红黑正确性
- 在二叉树中加入红黑平衡对平均执行效率只有很小的负面影响,然而却避免了对有序的数据操作的最坏的性能。