二叉树-详解平衡二叉排序树AVL
篇一:二叉树-遍历终极版
篇二:二叉树-创建、重建、转化
篇三:二叉树-详解二叉排序树
篇四:二叉树-详解平衡二叉树AVL
篇五:二叉树-常见简单算法题
平衡二叉搜索树AVL
也许因为输入值不够随机,也许因为输入顺序的原因,还或许一些插入、删除操作,会使得二叉搜索树失去平衡,造成搜索效率低落的情况。
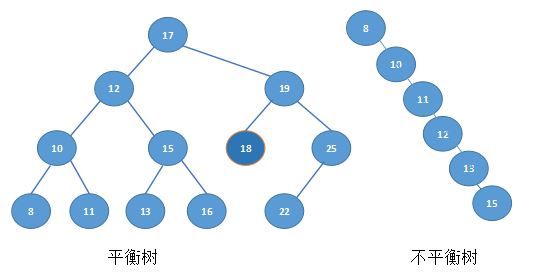
比如上面两个树,在平衡树上寻找15就只要2次查找,在非平衡树上却要5次查找方能找到,效率明显下降。
那么什么叫“平衡”,直观上的最佳平衡条件就是 每个节点的左右子树有着相同高度,但这确实太过苛刻。平衡二叉树AVL tree退而求其次,要求任何节点的左右节点的左右子树高度差不超过1。
定义平衡二叉树结构:
typedef struct BBSTNode
{
int data;
int bf;
struct BBSTNode*lchild, *rchild;
}AVLNode, *AVLTree;封装二叉排序树类:
class CAVLTree{
private:
//供内部调用的函数
int GetAVLHight(AVLTree T);//求得树的高度
void setHeight(AVLTree, int);//设置节点的高度值
//单旋转,右右插入导致的不平衡,左旋操作
void LL_RRotate(AVLTree *T);
//单旋转,右右插入导致的不平衡,左旋操作
void RR_LRotate(AVLTree *T);
//双旋转,左右插入导致的不平衡
void LR_Rotate(AVLTree *T);
//双旋转,右左插入导致的不平衡
void RL_Rotate(AVLTree *T);
public:
//默认构造函数
CAVLTree();
//析构函数
~CAVLTree();
//创建AVL树
void createAVLTree(int a[], int n);
//删除树
void deleteTree(AVLTree t);
//插入节点
AVLTree insertNode(AVLTree T, int val);
//删除树中元素值等于某值的节点
AVLTree deleteNode(AVLTree T, const int val);
//搜寻元素值等于某值的节点
AVLTree searchNode(AVLTree T, int val);
//前序遍历输出树
void PreOrderTraverse(AVLTree T);
//得到树中的元素值最大的节点
AVLTree FindMaxAVL(AVLTree T);
//得到树中的元素值最小的那个节点
AVLTree FindMinAVL(AVLTree T);
AVLTree T;
};1、二叉排序树失去平衡情况
举个因为插入元素使得平衡二叉树不平衡的情况:
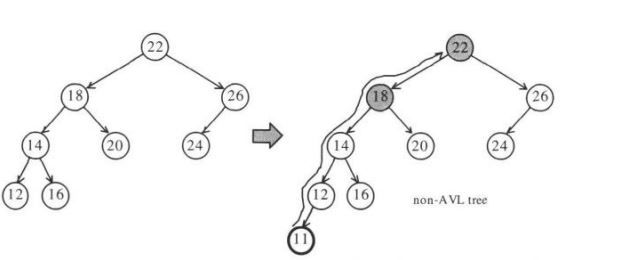
上图左边的二叉树本来是是个平衡二叉搜索树,因为各个节点的左右子树深度均不超多1,但是插入11后,树变成右图样子,图中灰色节点违反平衡条件。此时节点18的左右子树高度差为3-1=2>1;节点22的左右子树高度差为:4-2=2>1。
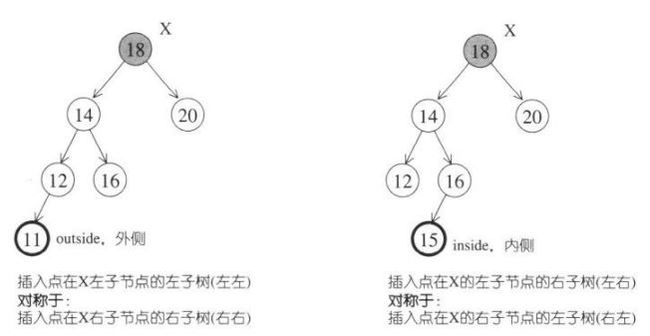
上述只是平衡被破坏的一种情况,这种情况是“左左插入”,还有三种情况(假设最深节点为X):
- 插入点位于X的左子节点的左子树——左左;
- 插入点位于X的左子节点的右子树——左右;
- 插入点位于X的右子节点的左子树——右左;
- 插入点位于X的右子节点的右子树——右右;
对于上面四中情况,我们再分一下类,可以分为两类:
1、外侧插入:左左、右右,很容易理解,都是在最边边上。
2、内侧插入:左右、右左,也很容易理解,网里面来了些。
既然树失去平衡了,那我们就要想办法让树恢复平衡啊!
2、二叉排序树恢复平衡方法
对于上面说到的外侧插入,我们可以采用单旋转操作调整解决;对于内侧插入,我们可以双旋转操作解决。
2.1、单旋转
先上个单旋转图,再慢慢解释:
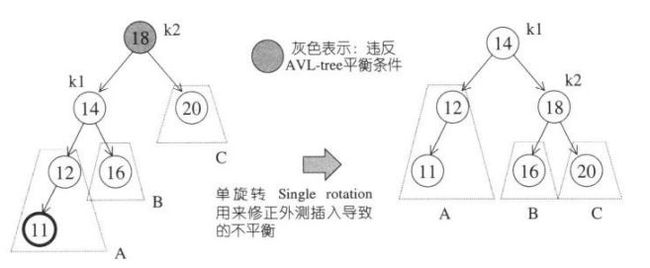
上图中11是外侧插入,11插入后,A子树的深度增加了一层,致使18节点的左子树深度增加一层,18节点变得不平衡了。为了调整平衡,我们希望将A子树提高一层,并将C子树下降一层。我们可以这么想象,把k1向上提起,使k2自然下滑,并将B子树挂到k2的左侧。
为什么这么做了,我们来回想一下二叉排序树的性质
1、根据性质我们知道,k2>k1,所以k2必须成为新树形中的k1节点的右子节点。(k1向上提起,使k2自然下滑)
2、同样根据性质,我们知道B子树的所有节点的键值都在k1和k2之间,也就是大于k1,小于k2,那不就是在k1的右子树上,k2的左子树上,因此将B子树挂到k2的左侧(将B子树挂到k2的左侧)。
最终调整后的图如上右图,这是“左左”,“右右”跟这情况一样。
单旋转,左左插入导致的不平衡,右旋操作:
void CAVLTree::LL_RRotate(AVLTree *p)
{
AVLTree N = (*p)->lchild;
(*p)->lchild = N->rchild;
N->rchild = (*p);
*p = N;
}单旋转,右右插入导致的不平衡,左旋操作:
void CAVLTree::RR_LRotate(AVLTree *p)
{
AVLTree N = (*p)->rchild;
(*p)->rchild = N->lchild;
N->lchild = (*p);
*p = N;
}2.2、双旋转
先上图,再解释:
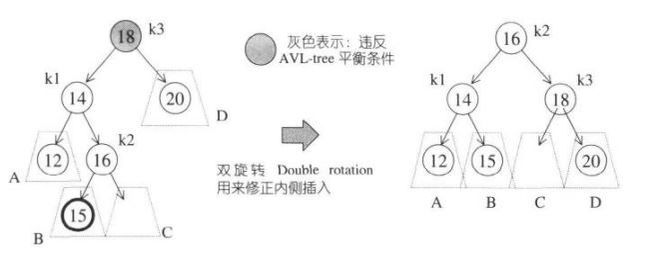
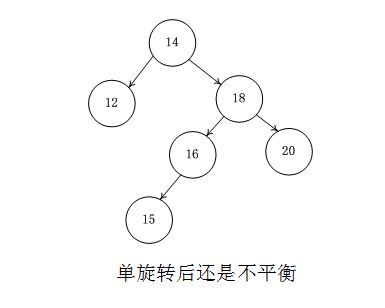
上图左图插入了元素15,造成了不平衡,这是内侧插入(左右)造成的不平衡,单旋转无法解决这种情况。因为单旋转之后还是不平衡的。
那么我们怎样可使得这棵树恢复平衡了,唯一的可能就是以k2为新的根节点,这使得k1必须成为k2的左子节点,k3必须成为k2的右子节点,新的树如上上右图所示,满足了平衡条件。上面这个变换就是“双旋转”,为什么这么叫了,因为它可以由两次“单旋转”完成。再详细看看双旋转过程。
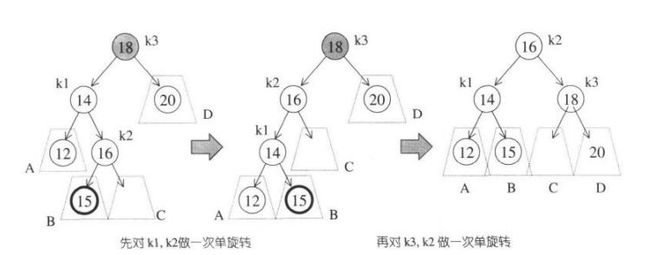
如上图,先对k1,k2这两节点做单旋转,的到中间那棵树,再对中间树上的k3,k2做一次单旋转,就可以得到平衡树了。
双旋转,左右插入导致的不平衡:
void CAVLTree::LR_Rotate(AVLTree *p)
{
//双旋转可以通过两次单旋转实现
//对p的左结点进行RR旋转,再对根节点进行LL旋转
RR_LRotate(&(*p)->lchild);
LL_RRotate(p);
}双旋转,右左插入导致的不平衡:
void CAVLTree::RL_Rotate(AVLTree *p)
{
LL_RRotate(&(*p)->rchild);
RR_LRotate(p);
}3、平衡二叉排序树插入
平衡二叉排序树的插入跟二叉排序树不同,它不能让二叉排序树失去平衡,代码如下:
AVLTree CAVLTree::insertNode(AVLTree T, int val)
{
AVLNode *pNewNode = new AVLNode;
pNewNode->data = val;
pNewNode->lchild = NULL;
pNewNode->rchild = NULL;
if (NULL == T)
{
T = pNewNode;
return T;
}
//需要插入节点的树非空
//插入的元素已经存在于树中,不符合要求
if (val == T->data)
{
cout << "元素中有重复,构建AVL树失败!" << endl;
return T;
}
//要插入的值小于根节点的值,将其插入左子树中
if (val < T->data)
{
//将其插入根节点的左子树中
T->lchild = insertNode(T->lchild, val);
//判断平衡条件是否仍然满足
if (GetAVLHight(T->lchild) - GetAVLHight(T->rchild) > 1)
{
//分两种情况进行旋转操作
//插入点位于T的左子结点的左子树
if (val < T->lchild->data)
//实施单旋转-右旋转
LL_RRotate(&T);
else
//插入点位于T的左子结点的右子树,实施双右旋转
LR_Rotate(&T);
}
}
//要插入的值大于根节点的值,将其插入右子树中
if (val > T->data)
{
T->rchild = insertNode(T->rchild, val);
//判断平衡条件是否仍然满足
if (GetAVLHight(T->rchild) - GetAVLHight(T->lchild) > 1)
{
//节点插入到T的右子节点的右子树中
if (val > T->rchild->data)
//实施单旋转-左旋转
RR_LRotate(&T);
else
//节点插入到T的右子节点的左子树上
//实施双旋转-左旋转
RL_Rotate(&T);
}
}
return T;
}4、平衡二叉排序树删除节点
AVLTree CAVLTree::deleteNode(AVLTree root, const int val)
{
if (!root)
{
cout << "The tree is NULL, delete failed" << endl;
return root;
}
AVLTree searchedNode = searchNode(root, val);
//没有找到相应的节点,删除失败
if (!searchedNode)
{
cout << "Cann't find the node to delete " << val << endl;
return root;
}
//找到了需要删除的节点
//需要删除的节点就是当前子树的根节点
if (val == root->data)
{
//左右子树都非空
if (root->lchild && root->rchild)
{
//在高度更大的那个子树上进行删除操作
if (GetAVLHight(root->lchild) > GetAVLHight(root->rchild))
{
//左子树高度大,删除左子树中元素值最大的那个节点,同时将其值赋值给根节点
root->data = FindMaxAVL(root->lchild)->data;
root->lchild = deleteNode(root->lchild, root->data);
}
else{
//删除右子树中元素值最小的那个节点,同时将其值赋值给根节点
root->data = FindMinAVL(root->rchild)->data;
root->rchild = deleteNode(root->rchild, root->data);
}
}
else{
//左右子树中有一个不为空,那个直接用需要被删除的节点的子节点替换之即可
AVLTree oldNode = root;
root = (root->lchild ? root->lchild : root->rchild);
delete oldNode;//释放节点所占的空间
oldNode = NULL;
}
}
else if (val < root->data)//要删除的节点在左子树中
{
//在左子树中进行递归删除
root->lchild = deleteNode(root->lchild, val);
//判断是否仍然满足平衡条件
if (GetAVLHight(root->rchild) - GetAVLHight(root->lchild) > 1)
{
if (root->rchild->lchild > root->rchild->rchild)
{
//左双旋转
RL_Rotate(&root);
}
else//进行左单旋转
RR_LRotate(&root);
}
}
else//需要删除的节点在右子树中
{
root->rchild = deleteNode(root->rchild, val);
//判断是否满足平衡条件
if (GetAVLHight(root->lchild) - GetAVLHight(root->rchild) > 1)
{
if (GetAVLHight(root->lchild->rchild) > GetAVLHight(root->lchild->lchild))
//右双旋转
LR_Rotate(&root);
else
//右单旋转
LL_RRotate(&root);
}
}
return root;
}5、平衡二叉排序树其他操作
1、求树的高度
int CAVLTree::GetAVLHight(AVLTree T)
{
if (T == NULL)
return 0;
else
{
int left = GetAVLHight(T->lchild);
int right = GetAVLHight(T->rchild);
return 1 + max(left, right);
}
}2、查找节点
AVLTree CAVLTree::searchNode(AVLTree root, int val)
{
if (!root) return NULL;
//搜索到
if (val == root->data)
return T;
else if (val <root->data)
{
//在左子树中搜索
return searchNode(root->lchild, val);
}
else
{
//在右子树中搜索
return searchNode(root->rchild, val);
}
}
3、查找最大最小元素
AVLTree CAVLTree::FindMaxAVL(AVLTree p)
{
if (NULL==p) return NULL;
if (p->rchild == NULL)
return p;
return FindMaxAVL(p->rchild);
}
AVLTree CAVLTree::FindMinAVL(AVLTree p)
{
if (NULL == p)
return NULL;
if (p->lchild == NULL)
return p;
return FindMinAVL(p->lchild);
}4、先序遍历
void CAVLTree::PreOrderTraverse(AVLTree T)
{
if (T)
{
cout << T->data << " ";
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}6、平衡二叉排序树测试
6.1、完整代码
#include 