Golang学习之路 - LeetCode-Go-Learning 第五题. 最长回文子串
Golang 基础
- [5. Longest Palindromic Substring](https://leetcode.com/problems/longest-palindromic-substring/)
- 题目
- 解题思路
- 解决方案
- 1. 使用回文的特性
- 4ms范例 - Manacher's Algorithm 马拉车算法
- 编写测试的方法
- 总结
鸣谢: LeetCode-In-Go
5. Longest Palindromic Substring
题目
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example:
Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.
Example:
Input: "cbbd"
Output: "bb"
解题思路
题目要求寻找字符串中的最长回文。
当然,我们可以使用下面的程序判断字符串s[i:j+1]是否是回文。
func isPalindromic(s *string, i, j int ) bool {
for i < j {
if (*s)[i] != (*s)[j] {
return false
}
i++
j--
}
return true
}
但是,这样就没有利用回文的一下特点,假定回文的长度为l,x为任意字符
- 当l为奇数时,回文的
正中间段只会是,“x”,或“xxx”,或“xxxxx”,或… - 当l为偶数时,回文的
正中间段只会是,“xx”,或“xxxx”,或“xxxxxx”,或… - 同一个字符串的任意两个回文substring的
正中间段,不会重叠。
我们在接下来的学习中将会使用该特性进行编码。
解决方案
1. 使用回文的特性
// 直接学习别人的写法
func longestPalindrome(s string) string {
if len(s) < 2 { // 肯定是回文,直接返回,空和单个字符
return s
}
// 最长回文的首字符索引,和最长回文的长度
begin, maxLen := 0, 1
// 在 for 循环中
// b 代表回文的**首**字符索引号,
// e 代表回文的**尾**字符索引号,
// i 代表回文`正中间段`首字符的索引号
// 在每一次for循环中
// 先从i开始,利用`正中间段`所有字符相同的特性,让b,e分别指向`正中间段`的首尾
// 再从`正中间段`向两边扩张,让b,e分别指向此`正中间段`为中心的最长回文的首尾
for i := 0; i < len(s); { // 以s[i]为'正中间段'首字符开始寻找最长回文。
if len(s) - i <= maxLen/2 {
// 因为i是回文`正中间段`首字符的索引号
// 假设此时能找到的最长回文的长度为l, 则,l <= (len(s)-i)*2 - 1
// 如果,len(s)-i <= maxLen/2 成立
// 则,l <= maxLen - 1
// 则,l < maxLen
// 所以,无需再找下去了。
break
}
// 相同连续字符的判断并向后移动
b, e := i, i
for e < len(s) - 1 && s[e+1] == s[e] {
e++
// 循环结束后,s[b:e+1]是一串相同的字符串
}
// 下一次回文的`正中间段`的首字符指挥室s[e+1]
// 为下一次循环做准备
i = e + 1
for e < len(s) - 1 && b > 0 && s[e + 1] == s[b - 1] {
e++
b--
// 循环结束后,s[b:e+1]是这次能找到的最长回文。
}
newLen := e + 1 - b
// 创新记录的话,就更新对应的记录
if newLen > maxLen {
begin = b
maxLen = newLen
}
}
return s[begin: begin+maxLen]
}
4ms范例 - Manacher’s Algorithm 马拉车算法
参考题解
为了改进暴力法,我们首先观察如何避免在验证回文时进行不必要的重复计算。考虑 \textrm{“ababa”}“ababa” 这个示例。如果我们已经知道 \textrm{“bab”}“bab” 是回文,那么很明显,\textrm{“ababa”}“ababa” 一定是回文,因为它的左首字母和右尾字母是相同的。
我们给出 P ( i , j ) P(i,j) P(i,j)的定义如下:

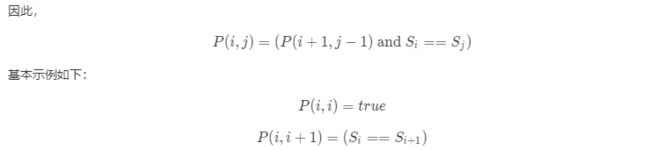
这产生了一个直观的动态规划解法,我们首先初始化一字母和二字母的回文,然后找到所有三字母回文,并依此类推…
作者:LeetCode
链接:https://leetcode-cn.com/problems/two-sum/solution/zui-chang-hui-wen-zi-chuan-by-leetcode/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
复杂度分析
- 时间复杂度: O ( n 2 ) O(n^2) O(n2), 这里给出我们的运行时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( n 2 ) O(n^2) O(n2), 该方法用 O ( n 2 ) O(n^2) O(n2)的控件来存储表。
// 返回最小值
// TODO: 这个算法需要详细理解一下。
func min(num1 int, num2 int) int{
if num1 < num2 {
return num1
}
return num2
}
// 此处采用的是动态规划法
func longestPalindrome(s string) string {
// 空串直接返回,这里可以优化为:
// if len(s) < 2 { // 肯定是回文,直接返回,空和单个字符
// return s
// }
if len(s) == 0 {
return ""
}
// 定义动态规划存储表
radius := make([] int, 2*len(s)+1)
var c int = -1
var R int = -1
var maxLength = 0;
var res string = "";
for i:=0;i<2*len(s)+1;i++ {
if (i<R && 2*c-i>=0){
radius[i] = min(R-i+1, radius[2*c-i])
} else {
radius[i] = 1
}
for p:=radius[i]; i-p>=0 && i+p<=2*len(s);p++ {
if (i-p) % 2 == 0 || s[(i-p)/2] == s[(i+p)/2]{
radius[i]++
c = i
R = i + p
} else {
break
}
}
if radius[i] > maxLength{
maxLength = radius[i]
res = s[(i-radius[i]+1)/2:(i+radius[i]-1)/2]
}
}
return res
}
编写测试的方法
package problem0005
import (
"testing"
"github.com/stretchr/testify/assert"
)
type para struct {
one string
}
type ans struct {
one string
}
type question struct {
p para
a ans
}
func Test_OK(t *testing.T) {
ast := assert.New(t)
qs := []question{
question{
p: para{
one: "babad",
},
a: ans{
one: "bab",
},
},
question{
p: para{
one: "cbbd",
},
a: ans{
one: "bb",
},
},
question{
p: para{
one: "abbcccddcccbba",
},
a: ans{
one: "abbcccddcccbba",
},
},
question{
p: para{
one: "a",
},
a: ans{
one: "a",
},
},
}
for _, q := range qs {
a, p := q.a, q.p
ast.Equal(a.one, longestPalindrome(p.one), "输入:%v", p)
}
}
总结
充分利用查找对象的特点,可以加快查找速度。