从零开始手写VIO第一章作业(含详细推导过程)
文章目录
- 前言·与同主题博文的不同之处
- 1.VIO 文献阅读
- 2.四元数和李代数更新
- 2.1理论依据
- 2.2代码实现
- 3.其他导数
- 3.1第一题
- 3.2第二题
前言·与同主题博文的不同之处
贺一家、高翔、崔华坤老师在深蓝学院开设了vSLAM进阶课程《从零开始手写VIO》,课程相当火爆,已经有数篇关于第一章作业的优秀博文。不过小编觉得还可以从两个方面进一步优化这个主题的博文。首先,第二道编程题和第三道公式推导题中涉及到的理论依据和参考资料可以明确给出,给出公式推导每一行对应的理论依据,具体到哪一本书的哪一个公式,这样对新手更加友好,其次,第二道编程题不少博文中直接使用Sophus库完成旋转矩阵更新,而Sophus库是利用Eigen库中的四元数来求解的,本质上依然是采用的四元数更新,并不是旋转矩阵更新。
有理解不到位的地方,欢迎大家指出!
1.VIO 文献阅读
第一题文献阅读参考之前的优秀博文《视觉SLAM进阶:从零开始手写VIO》第一讲作业
2.四元数和李代数更新
2.1理论依据
对于旋转矩阵更新R ← \leftarrow ←Rexp(w ∧ ^{\wedge} ∧),最重要的是将exp(w ∧ ^{\wedge} ∧)转换成对应的旋转矩阵,这里的理论依据是高翔老师《视觉 SLAM 十四讲》P72的公式,
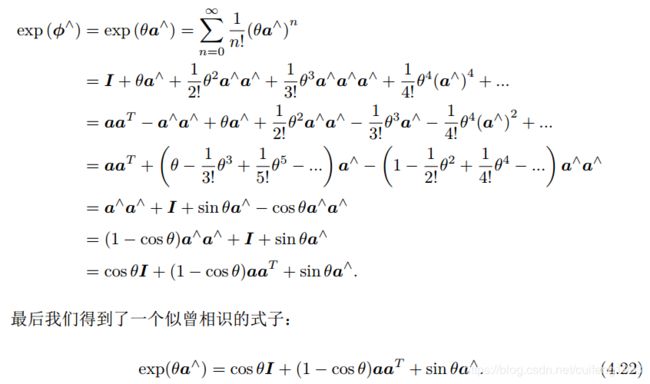
正如书中所说该公式也就是该书P51中所说的罗德里格斯公式(Rodrigues’s Formula ):

小编认为,旋转矩阵更新不能用Sophus库,查看《视觉 SLAM 十四讲》提供的第三方库Sophus的源码,Sophus 是利用的 Eigen 库中的四元数来完成旋转更新的,本质上是采用的四元数更新理论,而不是旋转矩阵更新理论。具体参考Sophus库中的源码文件so3.cpp和so3.h。更多详细的说明见代码中的注释。
2.2代码实现
#include <iostream>
#include<Eigen/Core>
#include<Eigen/Geometry>
using namespace std;
int main(int argc, char **argv) {
//变量初始化
Eigen::Vector3d w(0.01,0.02,0.03);//小量角速度(旋转向量)
Eigen::Matrix3d R=Eigen::AngleAxisd(M_PI/4,Eigen::Vector3d(0,0,1)).toRotationMatrix();//初始旋转矩阵,绕Z轴旋转45°
Eigen::Quaterniond q(R);//初始四元数
cout<<"初始旋转矩阵:"<<endl;
cout<<R<<endl;
cout<<"初始四元数:"<<endl;
cout<<q.coeffs().transpose() <<endl;
//利用Rodrigues's formula完成旋转矩阵更新
double theta=w.norm();//旋转向量对应的旋转角
Eigen::Vector3d n_w=w/theta;//归一化得到旋转向量对应的旋转轴
Eigen::Matrix3d n_w_skew;
n_w_skew<< 0, -n_w(2), n_w(1),
n_w(2), 0, -n_w(0),
-n_w(1), n_w(0), 0;
Eigen::Matrix3d R_w=cos(theta)*Eigen::Matrix3d::Identity()+(1-cos(theta))*n_w*n_w.transpose()+sin(theta)*n_w_skew;//Rodrigues's formula
Eigen::Matrix3d R_update=R*R_w;
cout<<"更新后的旋转矩阵:"<<endl;
cout<<R_update<<endl;
//四元数更新
Eigen::Quaterniond q_w(1,w(0)/2,w(1)/2,w(2)/2);//小量角速度对应的四元数
Eigen::Quaterniond q_update=q*q_w;
q_update=q_update.normalized();//单位四元数才可以表示三维旋转,所以必须归一化
cout<<"更新后的四元数:"<<endl;
cout<<q_update.coeffs().transpose() <<endl;
//计算两种方法得到的结果之差
cout<<"两种方法得到的结果之差:"<<endl;
cout<<q_update.toRotationMatrix()-R_update<<endl;
return 0;
}
CMakeLists.txt
cmake_minimum_required(VERSION 2.8)
project(qua_lie_update)
include_directories("/usr/include/eigen3")
add_executable(qua_lie_update main.cpp)
运行结果如下:
初始旋转矩阵:
0.707107 -0.707107 0
0.707107 0.707107 0
0 0 1
初始四元数:
0 0 0.382683 0.92388
更新后的旋转矩阵:
0.685368 -0.727891 0.0211022
0.727926 0.685616 0.00738758
-0.0198454 0.0102976 0.99975
更新后的四元数:
0.000792425 0.0111503 0.396472 0.917979
两种方法得到的结果之差:
2.5963e-06 2.37368e-06 -2.44789e-06
-2.38192e-06 2.53859e-06 -8.98416e-07
2.29623e-06 -1.23557e-06 5.83041e-08
可以看出两种更新方式差异很小,差异量级约为 10-6。
3.其他导数
先给出公式推导的详细过程,之后给出每一行对应的理论依据,具体到哪一本书的哪一个公式。
3.1第一题
公式推导:
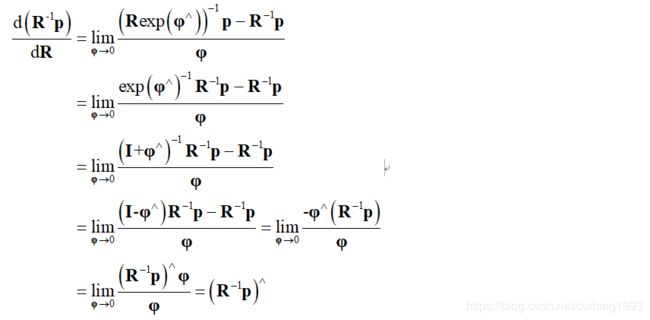
理论依据,公式的第二行到第五行分别用的如下性质一到性质四:

3.2第二题
公式推导:
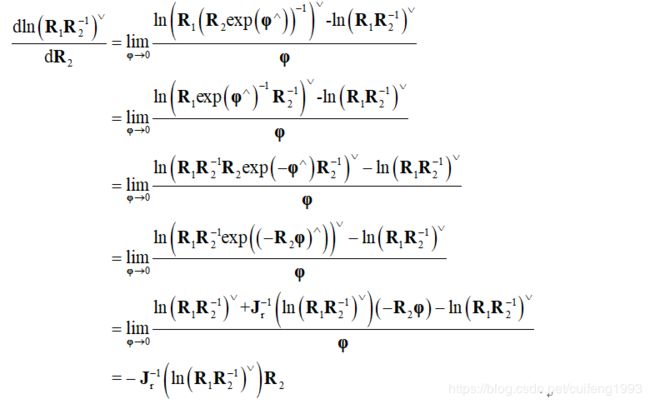
下面只给出3.1中没有涉及到的理论依据。第三行到第四行用了SO(3)的伴随性质,具体参考《视觉 SLAM 十四讲》P84习题5和6。

具体证明过程参考《视觉slam十四讲》第4讲课后习题_(∠ゝз:)_。
第四行到第五行用了如下性质:
![]()
理论依据见《视觉 SLAM 十四讲》P75公式(4.29)。
