人智导(五):对抗搜索与博弈
人智导(五):对抗搜索与博弈
对抗搜索
对抗搜索(adversarial search)源于博弈(game playing)
- 在多agents环境下,其它agent行动的不可预测性把不确定因素引入问题求解过程中
- 博弈:竞争环境下的零和(zero-sum)游戏,两个agents轮流行棋(博弈),动作(行棋)有限并确定,环境完全可观测
- 博弈结果:输、赢、平局
面对的挑战 - 如国际象棋,搜索树平均分支35,每个agent平均下50步,搜索树大致包括 3 5 100 35^{100} 35100个节点
- 限定时间内不可能计算出最佳决策情况下,如何做出较好的决策
博弈问题
博弈问题定义为搜索问题:
- S 0 S_0 S0:初始状态(initial state)表示博弈开始时的状态
- PLAYER(s):在状态s下应该行棋的agent(下文用Max或Min表示)
- ACTIONS(s):在s状态下可执行的动作集合
- RESULT(s, a):transition model得到一步行棋的结果状态
- TERMINAL-TEST(s):检测是否为博弈的结束状态(terminal state)
- UTILITY效用函数:对博弈结果状态给出分值(如:赢棋+1,输棋-1,和棋0)(初始状态、ACTIONS和RESULT定义了博弈树)
- 对于一个棋手(agent)而言,搜索就是发现一个策略(policy): ∀ s . s → a \forall s. s\to a ∀s.s→a
博弈树
下图为井字棋游戏的博弈树(utility值针对的是MAX棋手,MIN的值正好相反)

博弈树较小, 9 ! = 362880 9!=362880 9!=362880个结束状态,对于国际象棋等现实问题来说很小
资源有限的条件下搜索尽可能多的节点(而非所有)以决定棋手如何行棋(最佳还是合理?)
对抗搜索:Minimax算法
- 标准搜索(single agent): 最优解(optimal solution):即初始状态到目标状态且路径代价最小的动作序列
- 对抗搜索(two players: agent MAX, opposite MIN)
- 初始状态:对于MAX
- 结束状态:Utility作为状态值,针对MAX
- 中间状态:Minimax作为状态值,分别针对MAX和MIN
- 最优决策: ∀ s . s → a \forall s.s\to a ∀s.s→a
- MAX行棋,选其后继节点Minimax值最大的状态
- MIN行棋,选后继节点状态Minimax值最小的状态
算法思路:
M I N I M A X ( s ) = { U T I L I T Y ( s ) i f T E R M I N A L − T E S T ( s ) m a x a ∈ A c t i o n s ( s ) M I N I M A X ( R E S U L T ( s , a ) ) i f P L A Y E R ( s ) = M A X m i n a ∈ A c t i o n s ( s ) M I N I M A X ( R E S U L T ( s , a ) ) i f P L A Y E R ( s ) = M I N MINIMAX(s)=\begin{cases}UTILITY(s) & if~TERMINAL-TEST(s)\\ max_{a\in Actions(s)}MINIMAX(RESULT(s,a)) & if~PLAYER(s)=MAX\\ min_{a\in Actions(s)}MINIMAX(RESULT(s,a)) & if~PLAYER(s)=MIN \end{cases} MINIMAX(s)=⎩⎪⎨⎪⎧UTILITY(s)maxa∈Actions(s)MINIMAX(RESULT(s,a))mina∈Actions(s)MINIMAX(RESULT(s,a))if TERMINAL−TEST(s)if PLAYER(s)=MAXif PLAYER(s)=MIN
示意图:
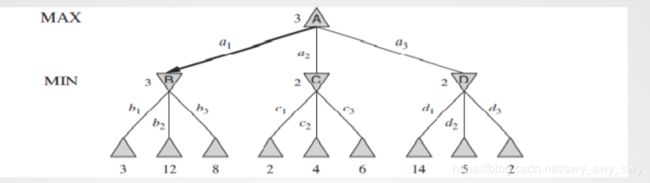
算法:
Function MINIMAX_DECISION(state) returns an action
return arg max MIN-VALUE(RESULT(state,a))
Function MAX-VALUE(state) returns a utility value
if TERMINAL-TEST(state) then return UTILITY(state)
v <--- oo
for each a in ACTIONS(state) do
v <--- MAX(v,MIN-VALUE(RESULT(s,a)))
return v
Function MIN-VALUE(state) returns a utility value
if TERMIANL-TEST(state) then return UTILITY(state)
v <--- oo
for each a in ACTIONS(state) do
v <--- MIN(v,MAX-VALUE(RESULT(s,a)))
return v
特点:
递归算法(自上而下至叶子节点,通过树把各节点minimax值回传)
完善博弈树的深度优先(depth-first)搜索过程
时间复杂度: O ( b m ) O(b^m) O(bm)
空间复杂度: O ( b m ) O(bm) O(bm)
博弈树的裁剪: α − β \alpha -\beta α−β剪枝
为什么需要裁剪:
- Minimax搜索算法的问题:博弈树的状态节点是指数级的
- 不探查博弈树所有节点的情况下,如何计算出正确的Minimax策略
- 提高效率:树裁剪(pruning)
- α − β \alpha -\beta α−β剪枝:Minimax搜索过程中,裁剪一部分树分支而不影响最终决策
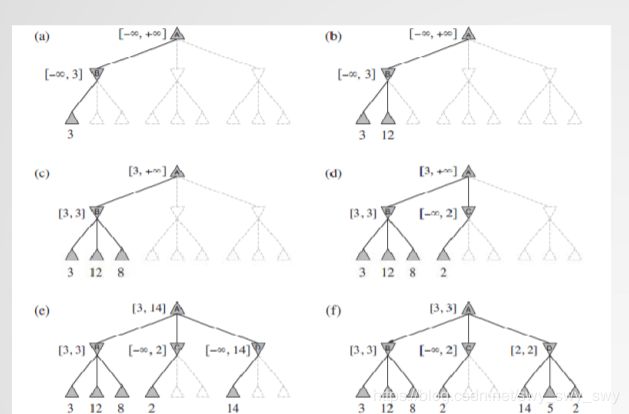
示例
- α \alpha α:对MAX而言,minimax搜索途径中当前所能发现的最高值
- β \beta β:对MIN而言,minimax搜索途径中当前所能发现的最低值
- 搜索过程中实时更新 α \alpha α值与 β \beta β值。如果当前节点的状态值对MAX(或MIN)而言差于 α \alpha α(或 β \beta β),则裁剪其余分支。
算法
Function ALPHA-BETA-SEARCH(state) returns an action
v <--- MAX-VALUE(state, -oo,+oo)
return the action in ACTIONS(state) with value v
Function MAX-VALUE(state, alpha, beta) returns a utility value
if TERMINAL-TEST(state) then return UTILITY(state)
v <--- -oo
for each a in ACTIONS(state) do
v <--- MAX(v, MIN-VALUE(RESULT(s,a),alpha,beta))
if v >= beta then return v
alpha <--- MAX(aalpha,v)
return v
Function MIN-VALUE(state, alpha, beta) returns a utility value
if TERMINAL-TEST(state) then return UTILITY(state)
v <--- +oo
for each a in ACTIONS(state) do
v <--- MIN(v,MAX_VALUE(RESULT(s,a),alpha,beta))
if v <= alpha then return v
beta <--- MIN(beta,v)
return v
特点: α − β \alpha -\beta α−β剪枝效果很大程度上依赖于状态节点被探查的次序。
博弈中的实时性约束
- Minimax算法:探查完整博弈状态空间(指数级)
- α − β \alpha -\beta α−β搜索:裁剪部分状态空间(real-time决策仍不现实)
- 限定搜索深度:解决决策的实时性(有限时间内必须行动:最优决策or合理决策)
- 启发式方法:及早评估及回溯搜索(如何有效地把中间节点状态转变为结束状态)
一些改进
启发式H-Minimax搜索
- 启发式(评估)函数EVAL替代Utility函数
- cutoff test 替代terminal test
- H − M I N I M A X ( s , d ) = { E V A L ( s ) i f C U T O F F − T E S T ( s , d ) m a x a ∈ A c t i o n s ( s ) H − M I N I M A X ( R E S U L T ( s , a ) , d + 1 ) i f P L A Y E R ( s ) = M A X m i n a ∈ A c t i o n s ( s ) H − M I N I M A X ( R E S U L T ( s , a ) , d + 1 ) i f P L A Y E R ( s ) = M I N H-MINIMAX(s,d)= \begin{cases} EVAL(s) & if~CUTOFF-TEST(s,d)\\ max_{a\in Actions(s)} H-MINIMAX(RESULT(s,a),d+1) & if~PLAYER(s)=MAX \\ min_{a\in Actions(s)}H-MINIMAX(RESULT(s,a),d+1) & if~PLAYER(s)=MIN \end{cases} H−MINIMAX(s,d)=⎩⎪⎨⎪⎧EVAL(s)maxa∈Actions(s)H−MINIMAX(RESULT(s,a),d+1)mina∈Actions(s)H−MINIMAX(RESULT(s,a),d+1)if CUTOFF−TEST(s,d)if PLAYER(s)=MAXif PLAYER(s)=MIN
- 其中 d d d为定义的最大深度阈值
启发式评估函数
- 评估函数:估算出博弈中某一节点状态的utility期望值
- 博弈程序的质量取决于启发式评价函数的质量
- 什么是好的评价函数?准确估算出胜利的机会
- 线性或非线性回归方法: E V A L ( s ) = w 1 f 1 ( s ) + w 2 f 2 ( s ) + ⋯ + w n f n ( s ) = Σ i = 1 n w i f i ( s ) EVAL(s)=w_1f_1(s)+w_2f_2(s)+\dots +w_nf_n(s)=\Sigma^n_{i=1}w_if_i(s) EVAL(s)=w1f1(s)+w2f2(s)+⋯+wnfn(s)=Σi=1nwifi(s)
- 特征(features)和权重(weights)并非博弈规则,而源于经验
cutting off搜索
算法:
Function ALPHA-BETA-SEARCH(state) returns an action
v <--- MAX-VALUE(state, -oo,+oo)
return the action in ACTIONS(state) with value v
Function MAX-VALUE(state, alpha, beta) returns a utility value
if CUTOFF-TEST(state,depth) then return Eval(state)
v <--- -oo
for each a in ACTIONS(state) do
v <--- MAX(v, MIN-VALUE(RESULT(s,a),alpha,beta))
if v >= beta then return v
alpha <--- MAX(aalpha,v)
return v
Function MIN-VALUE(state, alpha, beta) returns a utility value
if CUTOFF-TEST(state,depth) then return Eval(state)
v <--- +oo
for each a in ACTIONS(state) do
v <--- MIN(v,MAX_VALUE(RESULT(s,a),alpha,beta))
if v <= alpha then return v
beta <--- MIN(beta,v)
return v
特点:
- 参数设定阈值 d d d:大于深度阈值 d d d时cutoff-test为true(阈值 d d d的选取依赖于棋手行棋限定的时间)
- 迭代深度优先策略:
- 可在迭代地限定深度条件下,进行最深度的完备搜索
- 迭代深度也便于确定节点探查次序,优化 α − β \alpha -\beta α−β剪枝
其它
- 博弈程序其它改进措施
- 搜索与look up查表方式相结合(开局与残局):组合策略
- 大多博弈情况,判定S->A最佳决策不现实,算法都是在做近似
- 非“零和”方式,也可以是共赢方式
- 例如结束状态的Utility设定为: ( v a = 1000 , v b = 1000 ) (v_a=1000,v_b=1000) (va=1000,vb=1000)
- 对两位agent而言,最佳状态就是使每位都达到状态值1000这个目标(需要合作)
- 博弈不仅限于2-players,也可以是n-players