NavMesh生成研究(四):凸多边形生成
本文翻译自:http://critterai.org/projects/nmgen_study/polygen.html
这篇文章描述了导航网格构建过程中的第四步:从代表轮廓的简单多边形生成凸多边形。从这一步开始,我们离开体素空间,回到向量空间。
源数据类:ContourSet
构造器类:PolyMeshFieldBuilder
数据类:PolyMeshField
如果你需要回忆这一步的大致过程,请回到总体概述。
概述
这一阶段的主要工作如下:
- 轮廓(contour)的顶点位于体素空间中,这就意味着它们的顶点是整数格式,且代表着离高度域原点的距离。因此轮廓的顶点数据要被转换成源几何体(source geometry)的向量空间坐标。
- 每个轮廓与其他轮廓完全独立。在这一阶段中,我们将重复的数据合并,并将所有数据汇总到一个网格中。
- 轮廓只保证可以代表简单多边形,即同时包括凸多边形(convex polygon)和凹多边形(concave polygon)。而后者对于导航网格是没有作用的。因此我们将根据实际需求将轮廓分割成凸多边形。
- 我们收集多边形之间邻接边的信息(多边形邻接信息)。
坐标转换和顶点数据合并是相对简单的过程。因此我们不再赘述。如果你对这些算法感兴趣,可以去查阅有完整文档的源代码。我们将重点放在凸多边形的分割上。对每个轮廓执行如下步骤:
- 三角化每个轮廓。
- 将三角形合并成最大可能的凸多边形。
在生成邻接连通信息之后,我们结束这一阶段。
三角化
三角化的实现过程是:遍历轮廓的所有边,对于每组三个顶点,判断是否能形成一个有效的内部三角形。对于所有潜在的候选者,选取形成最短新边的那一个。新的边被称作是“分割边”,或者简称“分割”(partition)。对剩余顶点继续这个过程,直至三角化完成。
为了提升性能,三角化在轮廓的xz平面投影下进行。
分步骤阐述:找到可能的分割方案。
选取最短的分割并形成三角形。除去无效的分割,生成新的可能的分割。
继续分割:
……直到三角化完成。
检测合法的分割
两个算法被用来判断一组三个顶点是否可形成有效的内部三角形。第一个执行速度快,而且能很快剔除那些完全位于多边形以外的分割。如果分割位于多边形内部,那么另一个更昂贵的算法被用来确保它不与任何现存的多边形边界相交。
内部角算法
这个算法有一点难描述。因此这里举了一些例子。首先是一个有效的分割。对于顶点A、B、C而言,AB是一种可能的划分:
从顶点A出发顺着相邻边界发出两条射线。如果分割的终点(顶点B)位于内部角中,那么这就是一个可能的有效分割。
第二个例子是同样的场景、不同的顶点。因为分割的终点(顶点B)位于内部角之外,所以它不可能是有效的分割。
边相交算法
这个算法容易理解多了。它仅仅是遍历多边形中所有的边,并检查可能的分割是否与它们中的任何一个相交。如果有,那么就不是一个有效分割。
只有两个算法都通过,才能认为分割是有效的。
合并成凸多边形
合并只能发生在由同一轮廓生成的多个多边形之间。不要尝试去合并两个相邻轮廓里的多边形。
请注意我已经切换到通用的形式“多边形”,而非三角形。最初的合并针对的都是三角形,但随着合并过程的深入,非三角形的多边形也可能被合并。
这个过程如下:
- 找到所有能够被合并的多边形。
- 从这个列表中,选取两个有最长公共边的多边形合并。
- 重复直至再没有可合并的多边形。
两个多边形想要合并,需要满足以下所有条件:
- 多边形共享一条边。
- 生成的多边形仍然是凸多边形。
- 生成的多边形边数不多于参数
maxVertsPerPoly
检查共享边和计算合并边数量都很容易。判断合并后的多边形是否为凸多边形则更复杂一点。这个判断过程的关键是共享的顶点。在合并后,两者都需要检查一下形状。如果都能形成内部锐角1,那么合并后的多边形仍然会是凸多边形。我们对每个共享的顶点做如下操作:
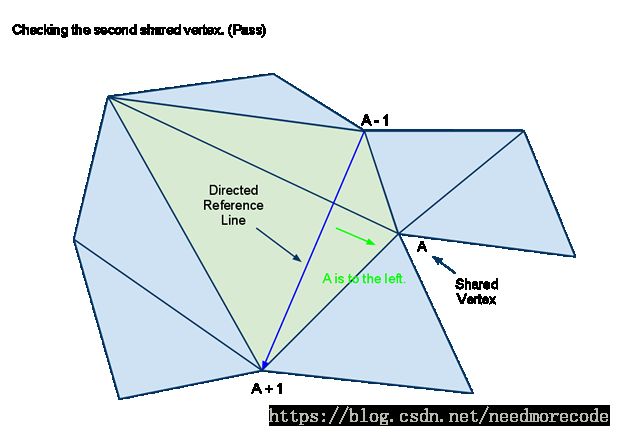
- 由共享顶点相邻前后的两个顶点构造一条有向的参考线(directed reference line)。
- 如果共享的顶点位于它的参考线左侧,那么就形成了一个锐角。
最好看图说话。第一个例子展示了一个有效的合并。
如果共享的顶点被标记为A,那么参考线则定为从顶点A-1到顶点A+1。顶点A处在参考线的左侧吗?
现在来看第二个共享的顶点。它是在参考线左侧吗?
在这下一个例子中,合并是无效的,因为合并后其中一个共享顶点形成的内部角是钝角2。
如果你对于用来检查点相对于有向线位置的算法不熟悉,那么可参见Soft Surfer算法。核心算法由PolyMeshFieldBuilder类中的getSignedAreaX2()函数来实现。
结尾
这个阶段的最后一步是遍历整个网格中的所有多边形,并生成连接信息。
当算法被优化后,从宏观上来讲,只需简单遍历所有的多边形边,并寻找与其有公共顶点的其他多边形。
目前的进展
我们最终回到了向量空间,并得到了一个由凸多边形构成的网格。
- 实际是指小于180度的角。 ↩
- 实际是指大于180度的角。 ↩