蓝桥杯 填空题
文章目录
- 1.高斯日记 (日期处理)
- 2.马虎的算式 (暴力)
- 3.第39级台阶 (dp)
- 4.黄金连分数 (高精度)
1.高斯日记 (日期处理)
问题描述:
大数学家高斯有个好习惯:无论如何都要记日记。
他的日记有个与众不同的地方,他从不注明年月日,而是用一个整数代替,比如:4210
后来人们知道,那个整数就是日期,它表示那一天是高斯出生后的第几天。这或许也是个好习惯,它时时刻刻提醒着主人:日子又过去一天,还有多少时光可以用于浪费呢?
高斯出生于:1777年4月30日。
在高斯发现的一个重要定理的日记上标注着:5343,因此可算出那天是:1791年12月15日。
高斯获得博士学位的那天日记上标着:8113
请你算出高斯获得博士学位的年月日。
提交答案的格式是:yyyy-mm-dd,例如:1980-03-21
请严格按照格式,通过浏览器提交答案。
注意:只提交这个日期,不要写其它附加内容,比如:说明性的文字。
方法一:编程
依据题意,可得如果日记上标注 1,则为1777-04-30。因为高斯把他出生算为一天!
首先要明确,不能用日期类API,因为日期类API都是从1970-1-1开始计算的,具体原因:为何计算机等电子设备要用1970年1月1日作参考时间
所以,我们模拟翻日历的过程来算日期,代码如下:
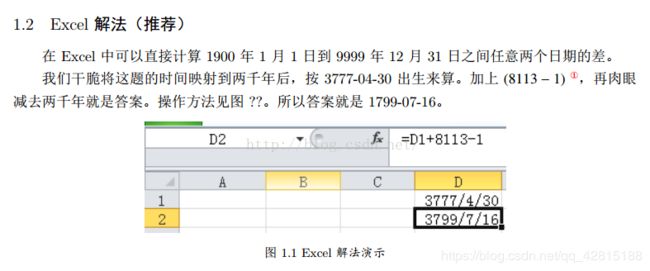
#include 方法二:excel
然而就本题来说,模拟翻日历的过程在考场上不要用编程来解决,手算+excel更快些:
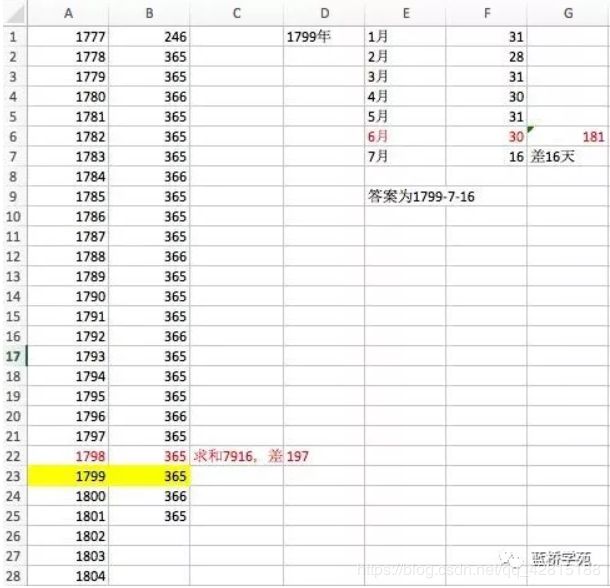
1777-4-30是第一天,这年过完,是第 x x x 天, x = 1 + 31 + 30 + 31 + 31 + 30 + 31 + 30 + 31 = 155 + 91 = 246 x=1+31+30+31+31+30+31+30+31=155+91=246 x=1+31+30+31+31+30+31+30+31=155+91=246
1778年365天
1779年365天
1780年366天
……
过完1798年共7916天,还差197天
1799年前六个月共181天,还差16天
因此答案为1799-7-16
最后一句:对于蓝桥杯省的填空题,excel是个很好的工具,特别是求和公式。
2.马虎的算式 (暴力)
问题描述:
小明是个急性子,上小学的时候经常把老师写在黑板上的题目抄错了。
有一次,老师出的题目是:36 x 495 = ?
他却给抄成了:396 x 45 = ?
但结果却很戏剧性,他的答案竟然是对的!!
因为 36 * 495 = 396 * 45 = 17820
类似这样的巧合情况可能还有很多,比如:27 * 594 = 297 * 54
假设 a b c d e 代表1~9不同的5个数字(注意是各不相同的数字,且不含0)
能满足形如: ab * cde = adb * ce 这样的算式一共有多少种呢?
请你利用计算机的优势寻找所有的可能,并回答不同算式的种类数。
满足乘法交换律的算式计为不同的种类,所以答案肯定是个偶数。
答案直接通过浏览器提交。
注意:只提交一个表示最终统计种类数的数字,不要提交解答过程或其它多余的内容。
代码:
#include3.第39级台阶 (dp)
问题描述:
小明刚刚看完电影《第39级台阶》,离开电影院的时候,他数了数礼堂前的台阶数,恰好是39级!
站在台阶前,他突然又想着一个问题:
如果我每一步只能迈上1个或2个台阶。先迈左脚,然后左右交替,最后一步是迈右脚,也就是说一共要走偶数步。那么,上完39级台阶,有多少种不同的上法呢?
请你利用计算机的优势,帮助小明寻找答案。
要求提交的是一个整数。
注意:不要提交解答过程,或其它的辅助说明文字。
代码:
#include4.黄金连分数 (高精度)
问题描述:
黄金分割数0.61803… 是个无理数,这个常数十分重要,在许多工程问题中会出现。有时需要把这个数字求得很精确。
对于某些精密工程,常数的精度很重要。也许你听说过哈勃太空望远镜,它首次升空后就发现了一处人工加工错误,对那样一个庞然大物,其实只是镜面加工时有比头发丝还细许多倍的一处错误而已,却使它成了“近视眼”!!
言归正传,我们如何求得黄金分割数的尽可能精确的值呢?有许多方法。
比较简单的一种是用连分数:

这个连分数计算的“层数”越多,它的值越接近黄金分割数。
请你利用这一特性,求出黄金分割数的足够精确值,要求四舍五入到小数点后100位。
小数点后3位的值为:0.618
小数点后4位的值为:0.6180
小数点后5位的值为:0.61803
小数点后7位的值为:0.6180340
(注意尾部的0,不能忽略)
你的任务是:写出精确到小数点后100位精度的黄金分割值。
注意:尾数的四舍五入! 尾数是0也要保留!
显然答案是一个小数,其小数点后有100位数字,请通过浏览器直接提交该数字。
注意:不要提交解答过程,或其它辅助说明类的内容。
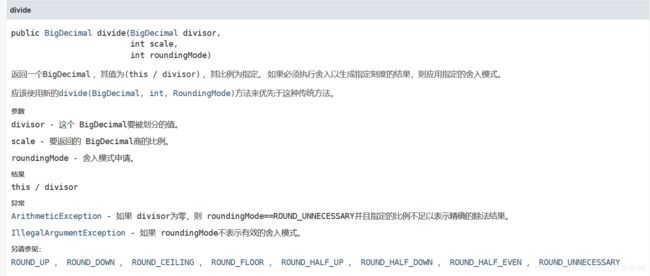
方法一:Java高精度
对Java而言,这道题只是考了BigDecimal和递归的使用。手动加深递归层数,直到不再变化为止。
import java.math.BigInteger; //大整数类
import java.math.BigDecimal; //大浮点数类
import java.util.*; //要用java.util包中的类Scanner
public class Main {
public static BigDecimal fun(int step) {
if(step>400) return BigDecimal.ONE;
return BigDecimal.ONE.divide(BigDecimal.ONE.add(fun(step + 1)), 100, BigDecimal.ROUND_HALF_UP);
}
public static void main(String[] args) {
System.out.println(fun(0));
}
}
//0.6180339887498948482045868343656381177203091798057628621354486227052604628189024497072072041893911375
方法二:斐波那契数列
下面解释一下黄金连分数和斐波那契数列的关系。
参考博客:https://www.cnblogs.com/youdiankun/p/4385515.html
这不是一个普通的分数,而是一个分母上有无穷多个 1 1 1 的繁分数,我们通常称这样的分数为“连分数”。
上述连分数可以看作是 x = 1 1 + x x = \frac{1}{1+x} x=1+x1中,把 x x x 的表达式反复代入等号右端得到的。例如,第一次代入得到的是 x = 1 1 + 1 1 + x x=\frac{1}{1+\frac{1}{1+x}} x=1+1+x11。
这一全部由 1 1 1 构成的连分数是最简单的一个连分数。
通常,求连分数的值,如同求无理数的值一样,我们常常需要求它的近似值。
如果把该连分数从第 n n n 条分数线截住,即把第 n + 1 n+1 n+1 条分数线上、下的部分都删去,就得到该连分数的第 n n n 次近似值,记作 u n v n \frac{u_n}{v_n} vnun

当 n n n 趋向于无穷大时,前一项与后一项的比值越来越逼近黄金分割 0.618 0.618 0.618
package test;
import java.math.BigInteger; //大整数类
import java.math.BigDecimal; //大浮点数类
import java.util.*; //要用java.util包中的类Scanner
public class Main {
public static void main(String[] args) {
BigInteger a = BigInteger.ONE; //常量 1
BigInteger b = BigInteger.ONE;
for(int i = 3; i < 500; i++) { //迭代求斐波那契数列
BigInteger c = a.add(b);
a = b;
b = c;
}
BigDecimal aa = new BigDecimal(a);
BigDecimal bb = new BigDecimal(b);
BigDecimal ans = aa.divide(bb, 100, BigDecimal.ROUND_HALF_UP);
System.out.println(ans);
}
}
//0.6180339887498948482045868343656381177203091798057628621354486227052604628189024497072072041893911375