2013第四届蓝桥杯JavaC组省赛真题
2013第四届蓝桥杯JavaC组省赛真题详解
第一题:猜年龄
题目描述
美国数学家维纳(N.Wiener)智力早熟,11岁就上了大学。他曾在1935~1936年应邀来中国清华大学讲学。一次,他参加某个重要会议,年轻的脸孔引人注目。于是有人询问他的年龄,他回答说:“我年龄的立方是个4位数。我年龄的4次方是个6位数。这10个数字正好包含了从0到9这10个数字,每个都恰好出现1次。”请你推算一下,他当时到底有多年轻。通过浏览器,直接提交他那时的年龄数字。
注意:不要提交解答过程,或其它的说明文字。
题解:直接由10到50进行遍历,用hashset存储每一位,特判一下a的3次方是不是4位数,a的4次方是不是6位数
import java.util.HashSet;
import java.util.Set;
public class Demo01 {
public static boolean checkNumber(int num){
Set<Integer> set = new HashSet<>();
int a = (int) Math.pow(num, 3);
int b = (int) Math.pow(num, 4);
if(String.valueOf(a).length() != 4) return false;
if(String.valueOf(b).length() != 6) return false;
while(a != 0){
set.add(a % 10);
a /= 10;
}
while(b != 0){
set.add(b % 10);
b /= 10;
}
if(set.size() == 10)
return true;
else
return false;
}
public static void main(String[] args) {
for (int i = 10; i < 50; i++) {
if(checkNumber(i)){
System.out.println(i);
break;
}
}
}
}
答案:18
第二题:组素数
题目描述
素数就是不能再进行等分的数。比如:2 3 5 7 11 等。 9 = 3 * 3 说明它可以3等分,因而不是素数。我们国家在1949年建国。如果只给你 1 9 4 9 这4个数字卡片,可以随意摆放它们的先后顺序(但卡片不能倒着摆放啊,我们不是在脑筋急转弯!),那么,你能组成多少个4位的素数呢?
比如:1949,4919 都符合要求。请你提交:能组成的4位素数的个数,不要罗列这些素数!!
注意:不要提交解答过程,或其它的辅助说明文字。
题解:对1,4,9,9这几个数字来一次全排列,但因为有数字相同,全排列就会有相同的数,所以拿一个hashset来解决数字重复的问题,数字全排列本人推荐使用dfs的方法
import java.util.Arrays;
import java.util.HashSet;
import java.util.Iterator;
import java.util.Set;
public class Demo02 {
static Set<Integer> set = new HashSet<>();
static boolean[] c = new boolean[5];
static int[] a = new int[5];
public static boolean isPrime(int num) {
if (num == 1 || num == 0)
return false;
for (int i = 2; i <= Math.sqrt(num); i++) {
if (num % i == 0)
return false;
}
return true;
}
public static void dfs(int b[], int start, int end) {
if (start == end) {
set.add(a[0] * 1000 + a[1] * 100 + a[2] * 10 + a[3] * 1);
} else {
for (int i = 0; i < end; i++) {
if (!c[i]) {
c[i] = true;
a[start] = b[i];
dfs(b, start + 1, end);
c[i] = false;
}
}
}
}
public static void main(String[] args) {
int[] b = { 1, 4, 9, 9 };
dfs(b, 0, b.length);
Iterator<Integer> it = set.iterator();
int count = 0;
while (it.hasNext()) {
int num = it.next();
if (isPrime(num))
count++;
}
System.out.println(count);
}
}
答案:6
第三题:马虎的算式
题目描述
小明是个急性子,上小学的时候经常把老师写在黑板上的题目抄错了。有一次,老师出的题目是:36 x 495 = ?他却给抄成了:396 x 45 = ? 但结果却很戏剧性,他的答案竟然是对的!! 因为 36 * 495 = 396 * 45 = 17820 类似这样的巧合情况可能还有很多,比如:27 * 594 = 297 * 54 假设 a b c d e 代表1~9不同的5个数字(注意是各不相同的数字,且不含0)
能满足形如: ab * cde = adb * ce 这样的算式一共有多少种呢?
请你利用计算机的优势寻找所有的可能,并回答不同算式的种类数。满足乘法交换律的算式计为不同的种类,所以答案肯定是个偶数。
答案直接通过浏览器提交。注意:只提交一个表示最终统计种类数的数字,不要提交解答过程或其它多余的内容。
题解:跟上面的题目差不多,直接一个dfs解决,但只需判断前5位。
public class Demo03 {
static boolean[] b = new boolean[10];
static int[] a = new int[10];
static int num;
public static void dfs(int start) {
if (start == 5) {
if ((a[0] * 10 + a[1]) * (a[2] * 100 + a[3] * 10 + a[4]) == (a[2] * 10 + a[4])
* (a[0] * 100 + a[3] * 10 + a[1])) {
num++;
return;
}
}
for (int i = 1; i < 10; i++) {
if (!b[i]) {
b[i] = true;
a[start] = i;
dfs(start + 1);
b[i] = false;
}
}
}
public static void main(String[] args) {
num = 0;
dfs(0);
System.out.println(num);
}
}
答案:142
第四题:第39级台阶
题目描述
小明刚刚看完电影《第39级台阶》,离开电影院的时候,他数了数礼堂前的台阶数,恰好是39级! 站在台阶前,他突然又想着一个问题: 如果我每一步只能迈上1个或2个台阶。先迈左脚,然后左右交替,最后一步是迈右脚,也就是说一共要走偶数步。那么,上完39级台阶,有多少种不同的上法呢?请你利用计算机的优势,帮助小明寻找答案。
要求提交的是一个整数。
注意:不要提交解答过程,或其它的辅助说明文字。
题解:到达第n级可分3种情况: (1)先偶数步到达n-2级,再跨1+1步 (2)先偶数步到达n-3级,再跨1+2或2+1步 (3)先偶数步到达n-4级,再跨2+2步 这样就有:f(n) = f(n-2) + 2 * f(n-3) + f(n-4); 初始条件为:f(1) = 0; f(2) = 1; f(3) = 2; f(4) = 2;
public class demo04 {
public static int fib(){
int []f = new int[41];
f[1] = 0;
f[2] = 1;
f[3] = 2;
f[4] = 2;
for(int i = 5; i < 40; i++){
f[i] = f[i-2]+2*f[i-3]+f[i-4];
}
return f[39];
}
public static void main(String[] args) {
System.out.println(fib());
}
}
答案:51167078
第五题:有理数类
有理数就是可以表示为两个整数的比值的数字。一般情况下,我们用近似的小数表示。但有些时候,不允许出现误差,必须用两个整数来表示一个有理数。 这时,我们可以建立一个“有理数类”,下面的代码初步实现了这个目标。为了简明,它只提供了加法和乘法运算。
class Rational
{
private long ra;
private long rb;
private long gcd(long a, long b){
if(b==0) return a;
return gcd(b,a%b);
}
public Rational(long a, long b){
ra = a;
rb = b;
long k = gcd(ra,rb);
if(k>1){ //需要约分
ra /= k;
rb /= k;
}
}
// 加法
public Rational add(Rational x){
return ________________________________________; //填空位置
}
// 乘法
public Rational mul(Rational x){
return new Rational(ra*x.ra, rb*x.rb);
}
public String toString(){
if(rb==1) return "" + ra;
return ra + "/" + rb;
}
}
使用该类的示例:
Rational a = new Rational(1,3);
Rational b = new Rational(1,6);
Rational c = a.add(b);
System.out.println(a + “+” + b + “=” + c);
请分析代码逻辑,并推测划线处的代码,通过网页提交
注意:仅把缺少的代码作为答案,千万不要填写多余的代码、符号或说明文字!!
class Rational {
private long ra;
private long rb;
private long gcd(long a, long b) {
if (b == 0)
return a;
return gcd(b, a % b);
}
public Rational(long a, long b) {
ra = a;
rb = b;
long k = gcd(ra, rb);
if (k > 1) { // 需要约分
ra /= k;
rb /= k;
}
}
// 加法
public Rational add(Rational x) {
return new Rational(ra * x.rb + x.ra * rb, rb * x.rb); // 填空位置
}
// 乘法
public Rational mul(Rational x) {
return new Rational(ra * x.ra, rb * x.rb);
}
public String toString() {
if (rb == 1)
return "" + ra;
return ra + "/" + rb;
}
}
public class Demo04 {
public static void main(String[] args) {
Rational a = new Rational(1, 3);
Rational b = new Rational(1, 6);
Rational c = a.add(b);
System.out.println(a + "+" + b + "=" + c);
}
}
答案:new Rational(ra * x.rb + x.ra * rb, rb * x.rb)
第六题:逆波兰表达式
题目描述
正常的表达式称为中缀表达式,运算符在中间,主要是给人阅读的,机器求解并不方便。 例如:3 + 5 * (2 + 6) - 1 而且,常常需要用括号来改变运算次序。相反,如果使用逆波兰表达式(前缀表达式)表示,上面的算式则表示为: - + 3 * 5 + 2 6 1 不再需要括号,机器可以用递归的方法很方便地求解。 为了简便,我们假设:
1. 只有 + - * 三种运算符
2. 每个运算数都是一个小于10的非负整数
下面的程序对一个逆波兰表示串进行求值。 其返回值为一个数组:其中第一元素表示求值结果,第二个元素表示它已解析的字符数。
static int[] evaluate(String x)
{
if(x.length()==0)
return new int[] {0,0};
char c = x.charAt(0);
if(c>='0' && c<='9') return new int[] {c-'0',1};
int[] v1 = evaluate(x.substring(1));
int[] v2 = __________________________________________; //填空位置
int v = Integer.MAX_VALUE;
if(c=='+') v = v1[0] + v2[0];
if(c=='*') v = v1[0] * v2[0];
if(c=='-') v = v1[0] - v2[0];
return new int[] {v,1+v1[1]+v2[1]};
}
请分析代码逻辑,并推测划线处的代码,通过网页提交。
注意:仅把缺少的代码作为答案,千万不要填写多余的代码、符号或说明文字!!
题解:一个二维数组,0代表最后的结果1代表有多少个字符。
public class Demo04 {
static int[] evaluate(String x) {
if (x.length() == 0)
return new int[] { 0, 0 };
char c = x.charAt(0);
if (c >= '0' && c <= '9')
return new int[] { c - '0', 1 };
int[] v1 = evaluate(x.substring(1));
int[] v2 = evaluate(x.substring(1 + v1[1])); // 填空位置
int v = Integer.MAX_VALUE;
if (c == '+')
v = v1[0] + v2[0];
if (c == '*')
v = v1[0] * v2[0];
if (c == '-')
v = v1[0] - v2[0];
return new int[] { v, 1 + v1[1] + v2[1] };
}
public static void main(String[] args) {
System.out.println(evaluate("-+3*5+261")[0]);
}
}
答案:evaluate(x.substring(1 + v1[1]))
第七题:核桃的数量
题目描述
小张是软件项目经理,他带领3个开发组。工期紧,今天都在加班呢。为鼓舞士气,小张打算给每个组发一袋核桃(据传言能补脑)。他的要求是: 1. 各组的核桃数量必须相同 2. 各组内必须能平分核桃(当然是不能打碎的)3. 尽量提供满足1,2条件的最小数量(节约闹革命嘛)
程序从标准输入读入:
a b c
a,b,c都是正整数,表示每个组正在加班的人数,用空格分开(a,b,c<30)
程序输出:
一个正整数,表示每袋核桃的数量。
例如:
用户输入:
2 4 5
程序输出:
20
再例如:
用户输入:
3 1 1
程序输出:
3
资源约定:
峰值内存消耗(含虚拟机) < 64M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
题解:这题相当于求3个数的最小公倍数,我只能说so easy
import java.util.Scanner;
public class Demo04 {
public static int gcd(int a, int b){
return b == 0 ? a : gcd(b,a%b);
}
public static int lcm(int a, int b){
return a * b / gcd(a,b);
}
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
while(cin.hasNext()){
int a = cin.nextInt();
int b = cin.nextInt();
int c = cin.nextInt();
System.out.println(lcm(a, lcm(b, c)));
}
}
}
第八题:打印十字图
小明为某机构设计了一个十字型的徽标(并非红十字会啊),如下所示(可参见p1.jpg)
对方同时也需要在电脑dos窗口中以字符的形式输出该标志,并能任意控制层数。 为了能准确比对空白的数量,程序要求对行中的空白以句点(.)代替。
输入格式:
一个正整数 n (n<30) 表示要求打印图形的层数
输出:
对应包围层数的该标志。
例如:
用户输入:
1
程序应该输出:

用户输入:
3
程序应该输出:

请仔细观察样例,尤其要注意句点的数量和输出位置。
资源约定:
峰值内存消耗(含虚拟机) < 64M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。

所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.6及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理
题解:做这道题看起来有点麻烦,其实还好,找到规律就简单了,首先咱们从中间看,每一个环离中间为2*i的距离,上下左右都一样,另外有4个特殊角,就特殊处理。
import java.util.Scanner;
public class Demo04 {
public static void getResult(int num){
int len = (4 * num + 5);
int mid = len / 2;
char [][]c = new char[len][len];
for(int i = 0; i < len; i++){
for(int j = 0; j < len; j++){
c[i][j] = '.';
}
}
for(int i = mid-2; i <= mid+2; i++){
c[mid][i] = '$';
c[i][mid] = '$';
}
for(int i = 1; i <= num; i++){
for(int j = mid - 2*i; j <= mid + 2*i; j++){
c[mid-2*(i+1)][j] = '$';
c[mid+2*(i+1)][j] = '$';
c[j][mid-2*(i+1)] = '$';
c[j][mid+2*(i+1)] = '$';
}
c[mid-2*i][mid-2*i] = '$';
c[mid-2*i-1][mid-2*i] = '$';
c[mid-2*i][mid-2*i-1] = '$';
c[mid+2*i][mid-2*i] = '$';
c[mid+2*i+1][mid-2*i] = '$';
c[mid+2*i][mid-2*i-1] = '$';
c[mid-2*i][mid+2*i] = '$';
c[mid-2*i-1][mid+2*i] = '$';
c[mid-2*i][mid+2*i+1] = '$';
c[mid+2*i][mid+2*i] = '$';
c[mid+2*i+1][mid+2*i] = '$';
c[mid+2*i][mid+2*i+1] = '$';
}
for(int i = 0; i < len; i++){
for(int j = 0; j < len; j++){
System.out.print(c[i][j]);
}
System.out.println();
}
}
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
while(cin.hasNext()){
int num = cin.nextInt();
getResult(num);
}
}
}
第九题:买不到的数目
题目描述
小明开了一家糖果店。他别出心裁:把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。小朋友来买糖的时候,他就用这两种包装来组合。当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
输入:
两个正整数,表示每种包装中糖的颗数(都不多于1000)
要求输出:
一个正整数,表示最大不能买到的糖数
不需要考虑无解的情况
例如:
用户输入:
4 7
程序应该输出:
17
再例如:
用户输入:
3 5
程序应该输出:
7
资源约定:
峰值内存消耗(含虚拟机) < 64M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.6及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
import java.util.Scanner;
public class Demo05 {
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
while(cin.hasNext()){
int a = cin.nextInt();
int b = cin.nextInt();
System.out.println(a*b-a-b);
}
}
}
第十题:剪格子
题目描述
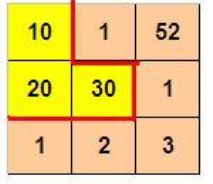
如图p1.jpg所示,3 x 3 的格子中填写了一些整数。我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是60。本题的要求就是请你编程判定:对给定的m x n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。 如果无法分割,则输出 0
程序输入输出格式要求:
程序先读入两个整数 m n 用空格分割 (m,n<10)表示表格的宽度和高度, 接下来是n行,每行m个正整数,用空格分开。每个整数不大于10000, 程序输出:在所有解中,包含左上角的分割区可能包含的最小的格子数目。
例如:
用户输入:
3 3
10 1 52
20 30 1
1 2 3
则程序输出:
3
再例如:
用户输入:
4 3
1 1 1 1
1 30 80 2
1 1 1 100
则程序输出:
10
资源约定:
峰值内存消耗(含虚拟机) < 64M
CPU消耗 < 5000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.6及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。

题解:这题就是一道简单的搜索题
import java.util.Scanner;
public class Demo05 {
static int num, n, m, sum;
static int[][] a = new int[10][10];
static boolean[][] v = new boolean[10][10];
public static boolean outBorder(int i, int j) {
if (i < 0 || j < 0 || i >= n || j >= m) {
return false;
}
return true;
}
public static void dfs(int i, int j, int currentNum, int currentSum) {
v[i][j] = true;
currentSum += a[i][j];
++currentNum;
if (currentSum * 2 >= sum) {
if (currentSum * 2 == sum) {
num = Math.min(currentNum, num);
}
v[i][j] = false;
return;
}
if (outBorder(i - 1, j) && !v[i - 1][j]) {
dfs(i - 1, j, currentNum, currentSum);
}
if (outBorder(i, j - 1) && !v[i][j - 1]) {
dfs(i, j - 1, currentNum, currentSum);
}
if (outBorder(i + 1, j) && !v[i + 1][j]) {
dfs(i + 1, j, currentNum, currentSum);
}
if (outBorder(i, j + 1) && !v[i][j + 1]) {
dfs(i, j + 1, currentNum, currentSum);
}
v[i][j] = false;
}
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
while (cin.hasNext()) {
m = cin.nextInt();
n = cin.nextInt();
sum = 0;
num = Integer.MAX_VALUE;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
a[i][j] = cin.nextInt();
sum += a[i][j];
}
}
if (sum % 2 == 1) {
System.out.println(0);
continue;
}
dfs(0, 0, 0, 0);
if (num == Integer.MAX_VALUE) {
System.out.println(0);
} else {
System.out.println(num);
}
}
}
}