【数学建模】灰色预测模型GM(1，1)附例题分析(MATLAB实现)

一、灰色预测概述

1.灰色系统、白色系统和黑色系统

• 系统：客观世界在不断发展变化的同时，往往通过事物之间及因素之间相互制约、相互联系而构成的一个整体
• 白色系统：具有较充足的信息量，其发展变化规律明显，定量描述较方便，结构与参数较具体的系统
• 黑色系统：内部特性全部未知的一个系统，只能通过它与外界的联系来加以观测研究
• 灰色系统：介于白色系统与黑色系统之间，无法建立客观的物理原型，其作用原理亦不明确，内部因素难以辨识或之间关系隐蔽，很难准确了解其的行为特征的系统

2.灰色系统与其它学科的比较

项目	灰色系统	概率统计	模糊数学
研究对象	贫信息不确定	随机不确定	认知不确定
基础集合	灰色朦胧集	康托集	模糊集
方法依据	信息覆盖	映射	映射
途径手段	灰序列算子	频率统计	截集
数据要求	任意分布	典型分布	隶属度可知
侧重点	内涵	内涵	外延
目标	现实规律	历史统计规律	认知表达
特色	小样本	大样本	凭经验

3.灰色预测分类及特点

灰色预测是用灰色模型GM(1,1)来进行定量分析的，通常分为以下几类：

• 灰色时间序列预测。用等时距观测到的反映预测对象特征的一系列数量（如产量、销量、人口数量、存款数量、利率等）构造灰色预测模型，预测未来某一时刻的特征量，或者达到某特征量的时间。
• 畸变预测（灾变预测）。通过模型预测异常值出现的时刻，预测异常值什么时候出现在特定时区内。
• 波形预测，或称为拓扑预测，它是通过灰色模型预测事物未来变动的轨迹。
• 系统预测，对系统行为特征指标建立一族相互关联的灰色预测理论模型，在预测系统整体变化的同时，预测系统各个环节的变化。
  特点：
• 允许少数据预测
• 允许对灰因果律事件进行预测
• 具有可检验性

---

二、灰色预测模型GM(1,1)

1.几个理论

通过对数列中的数据进行处理，产生新的数列，以此来挖掘和寻找数的规律性的方法叫做数的生成。

1.1 累加生成数（1-AGO)

记原始序列为：$$X^{(0)}=(x^{(0)}(1),x^{(0)}(2),.......,x^{(0)}(n))$$
一次累加生成序列为:$$X^{(1)}=(x^{(1)}(1),x^{(1)}(2),.......,x^{(1)}(n))$$
其中：$$x^{(1)}(k)=\sum _{i=0}^k{x}^{(0)}(i)=x^{(1)}(k-1)+x^{(0)}(k)$$

注：若实际数列中有负数，可使用移轴的方法，避免信息丢失。

1.2 累减生成数（IAGO）

累减生成数实质是累加生成数的逆运算。

记原始序列为：$$X^{(1)}=(x^{(1)}(1),x^{(1)}(2),.......,x^{(1)}(n))$$
一次累减生成序列 1-IAGO：$$X^{(0)}=(x^{(0)}(1),x^{(0)}(2),.......,x^{(0)}(n))$$
其中：
$$x^{(0)}(k)=x^{(1)}(k)+x^{(1)}(k-1)，k=2,3,.......,n$$

1.3 邻值生成数

令Z⁽¹⁾为X⁽¹⁾的紧邻均值（MEAN）生成序列:$$Z^{(1)}=(z^{(1)}(2),z^{(1)}(3),.......,z^{(1)}(n))$$
其中：$$z^{(1)}(k)=\alpha x^{(1)}(k)+(1-\alpha )x^{(1)}(k-1)，k=2,3,.......,n$$$\alpha$为生成系数，取0.5时，称生成的数列为均值生成数，也称等权邻值生成数。

2.GM(1,1)

基于上述几个概念，可以构建GM(1,1)模型。

2.1 灰微分方程模型

灰导数：$$d(k)=x^{(0)}(k)=x^{(1)}(k)-x^{(1)}(k-1)$$
结合邻值生成序列，定义GM(1,1)灰微分方程模型为：$$x^{(0)}(k)+a{z}^{(1)}(k)=b$$或$$d(k)+a{z}^{(1)}(k)=b$$
其中，a称为发展系数，z⁽¹⁾(k)称为白化背景值，b称为灰作用量。

现x⁽⁰⁾、z⁽¹⁾(k)为已知量，a、b待求解，故将k=2,3,…,n 待入，可得到矩阵方程$$\{\begin{array}{l}{x}^{(0)}(2)+a{z}^{(1)}(2)=b,\\ x^{(0)}(3)+a{z}^{(1)}(3)=b,\\ ......,\\ x^{(0)}(n)+a{z}^{(1)}(n)=b\end{array}$$
稍做转换：
$$\{\begin{array}{l}{x}^{(0)}(2)=-a{z}^{(1)}(2)+b,\\ x^{(0)}(3)=-a{z}^{(1)}(3)+b,\\ ......,\\ x^{(0)}(n)=-a{z}^{(1)}(n)+b\end{array}$$
令：$$u=\left[\begin{array}{c}a\\ b\end{array}\right]$$$$Y=\left[\begin{array}{c}{x}^{(0)}(2)\\ x^{(0)}(3)\\ ......\\ x^{(0)}(n)\end{array}\right]$$$$B=\left[\begin{array}{cc}-z^{(1)}(2)& 1\\ -z^{(1)}(3)& 1\\ ......& \\ -z^{(1)}(n)& 1\end{array}\right]$$
此时，GM(1,1)模型转化为Bu=Y，利用矩阵运算，解得：u=YB^-1。

2.2 白化方程

定义：对于GM（1，1）的灰微分方程，如果将时刻k=2,3,…,n视为连续变量t，则之前的x⁽¹⁾视为时间t函数，于是灰导数x⁽⁰⁾(k)变为连续函数的导数dx⁽¹⁾(t)/dt,白化背景值z⁽¹⁾(k)对应于导数x⁽¹⁾(t)。于是GM（1，1）的灰微分方程对应于的白微分方程为：$$\frac{d{x}^{(1)}(t)}{dt}+a{x}^{(1)}(t)=b$$解为：$$x^{(1)}(t)=(x^{(0)}(1)-\frac{b}{a})e^{-a(t-1)}+\frac{b}{a}$$
注意：此处得到的解为累加数列，后续需要将其转化为累减数列

3.算法步骤

3.1 数据的检验与处理

为了保证GM（1，1）建模方法的可行性，需要对已知数据做必要的检验处理。
计算数列的级比：$$\lambda (k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)},k=2,3,...,n$$
通过范围：（e^-2/(n+1),e^2/(n+2)）
否则需要对数列作平移变换，使级比落在范围中$$y^{(0)}(k)=x^{(0)}(k)+C,k=1,2,...,n$$

3.2 建立模型，求出预测值

通过对白化方程的解，进行累减，得到预测值。$$x^{(1)}(t)=(x^{(0)}(1)-\frac{b}{a})e^{-a(t-1)}+\frac{b}{a}$$$${\hat{x}}^{(1)}(k+1)=(x^{(0)}(1)-\frac{b}{a})e^{-ak}+\frac{b}{a}$$$${\hat{x}}^{(0)}(k)={\hat{x}}^{(1)}(k)+{\hat{x}}^{(1)}(k-1)，k=2,3,.......,n$$

3.3 检验预测值

• 计算相对残差$${\xi }_k=\frac{x^{(0)}(k)-{\hat{x}}^{(0)}(k)}{x^{(0)}(k)}$$
  若所有的|${\xi }_k$|<0.1，则认为达到较高的要求；
  若所有的|${\xi }_k$|<0.2，则认为达到一般的要求。
• 级比偏差值检验$$\rho (k)=1-\frac{1-0.5a}{1+0.5a}\lambda (k)$$
  若所有的|$\rho (k)$|<0.1，则认为达到较高的要求；
  若所有的|$\rho (k)$|<0.2，则认为达到一般的要求。

---

三、实例及MATLAB实现

在网上看了一些例题，大多都是可以直接通过级比检验不需要进行平移变换的，这里给出一题需要进行平移变换的，并附上级比检验不通过进行平移变换的代码。

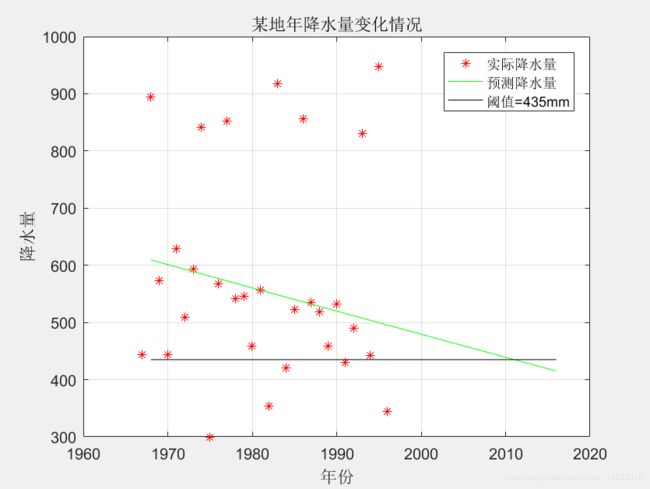
题目：某地年降水量原始数据序列如下表所示，根据多年的时间观测，每当年降水量小于430～440mm时，该地区将发生旱灾.所以，选择阈值=435mm, 利用GM(1,1)模型进行旱灾预报。
框架：

1.级比检测
   1.1求级比
   1.2级比判断
   1.3若级比检验未通过，则进行平行变换
2.GM(1,1)建模
   2.2AGO
   2.3加权邻值生成
   2.4%预测后续数据
3.检验预测值
4.作图

MATLAB实现：

%导入数据
x0=[444,895,573,443,629,509,594,842,300,567,852,542,546,459,557,354,917,421,522,856,535,518,459,532,430,490,830,442,948,344];
n=length(x0);
%求级比
lamda=x0(1:n-1)./x0(2:n);
%级比判断
range=minmax(lamda)
range1=[exp(-2/(n+1)),exp(2/n+2)]
flag=1;
if(range(1)>range1(1)&&range(2)range1(1)&&range(2)

---

参考文献：

• 【数学建模常用算法】之灰色预测模型
• 【数学建模】灰色预测及Python实现