三路快排算法加强版(三路快排的再次改进)
:不要忘记初心哈 :)
- 理论依据
- 快排算法的缺陷及其逐一改进
- 三路快排尽可能三等份划分区间
- 通过待排元素的区间长度划分?
- 通过待排元素的最值之差划分?
- 直接使用待排元素的最大值划分?
- 实验数据
- 大范围随机,重复元素极少
- 一千万数据
- 一个亿数据
- 小范围随机,大量重复元素
- 一千万数据
- 一个亿数据
- 当待排序的元素完全重复时
- 一千万数据
- 一个亿数据
- 当待排序的元素线性无重时
- 一千万数据
- 实验数据总结
- 通过实验发现的一些规律
- 关于实验数据疑惑的解答
- 代码实现
- 参考资料
理论依据
快排算法的缺陷及其逐一改进
关于快速排序,无论是单路还是双路亦或是三路快排,
有关其缺陷与优化办法,
我在之前的一篇文章里已经作出了详细解读.
具体链接如下:
快速排序(重温经典算法系列)
如何在 Partition操作时,尽可能地 —— 划分出
3等分的元素区间?
这边是三路快排的改进策略.
三路快排尽可能三等份划分区间
通过待排元素的区间长度划分?
思路1:
利用待排序的区间长度,实现三等分划分?
即:
(high - low)为当前待排序区间[low,high]的长度.
令之划分出三等分,然后再于中间部分随机选取 哨兵元素.
(int)((high - low)/3.0*1.0)
(int)((high - low)/3.0*2.0)
可行度:(1——5评价)
3 颗星
利弊分析
如此设计,仅会在元素值与其索引值存在某种关联时才会产生巨大的优化效果.
虽说完全有序的数据往往与数组索引值存在关联,
但是在处理其他完全随机或者元素随机范围不大的数据时,优化适得其反.
通过待排元素的最值之差划分?
思路1:
利用待排区间的最值元素之差,实现三等分划分?
即:
maxNum 和 minNum 分别存放当前待排序区间的最大和最小元素值,
令之划分出三等分,即
以 (maxNum - minNUm) 替代 (high - low),
然后再于中间部分随机选取 哨兵元素.
可行度:(1——5评价)
2 颗星
利弊分析
如此设计,
当区间元素范围较大时,多数情况下都会存在或多或少的优化效果.
可当区间元素范围较小时(此时待排序区间通常也相对较小),
优化操作并不明显甚至是适得其反,拖累程序性能.
快排到了中后期阶段,
待排序的区间往往会变得很小,其中的元素值也会大小不相上下,
这种情况下,
最值元素之差就变得很小了,此时优化操作变为拖累行为.
另外,
更不用说若给出的数据直接是范围极小、存在大量的重复元素的数组了,
如此情况下优化代码几乎没有用处,
加强版三路快排已经退化为三路快排,并且由于额外的设计开销导致算法性能大不如前.
更加地适得其反!!
严重拖累程序性能!!!
直接使用待排元素的最大值划分?
思路1:
直接利用待排区间的最大值元素,实现三等分划分?
即:
maxNum 和 minNum 分别存放当前待排序区间的最大和最小元素值,
但是 仅以 maxNum 替代 (high - low),
然后再于中间部分随机选取 哨兵元素.
可行度:(1——5评价)
5 颗星
利弊分析
经数据测试,这是一个普适版本的优化方式.
无论是元素完全随机的情况,
还是元素随机范围极小、存在大量重复元素的情况,
甚至是两两相等、元素完全重复的数据
亦或是元素直接等于其索引值、完全线性没有任何重复元素的情况,
或者是该情况元素先取反序之后再排序,
加强型三路快排都优胜与其他三种快排的设计.
这,
是我自己通过实验数据、反复操作尝试得到的优化结果.
暂无使得其性能下降的反例数据.
实验数据
大范围随机,重复元素极少
此种情况下有可能会存在少量的重复元素,不过
即使有往往也是极少的,
绝大多数情况下都不会多个重复的元素.
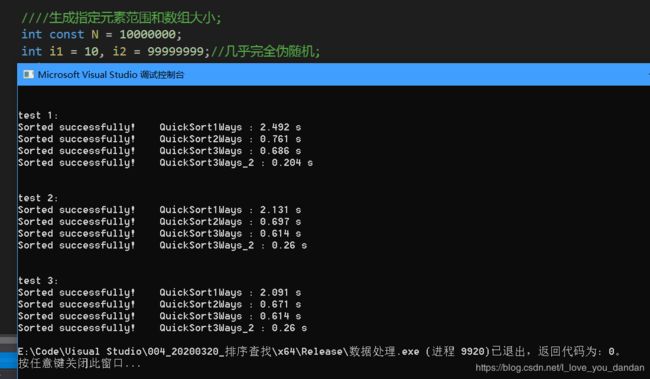
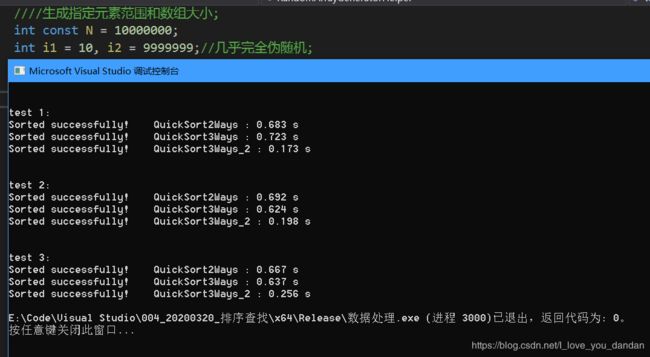
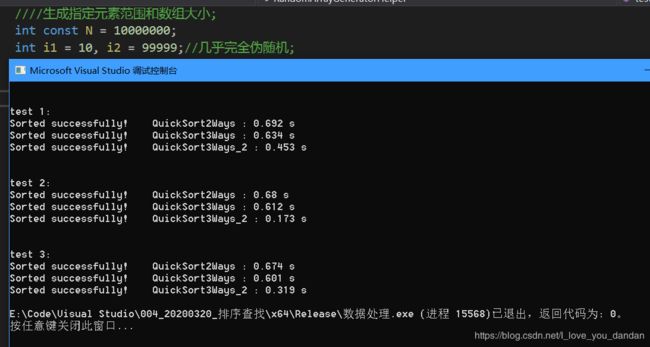
一千万数据
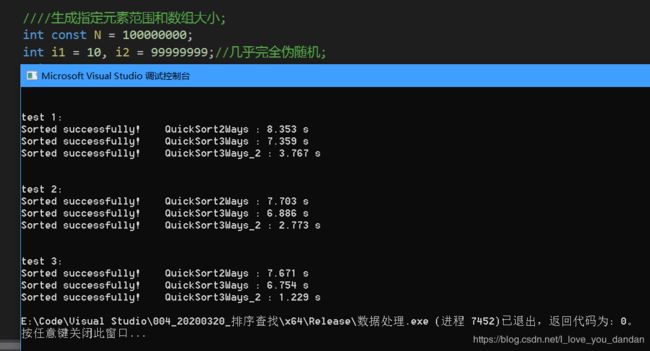
测试一:1千万数据,1亿范围随机
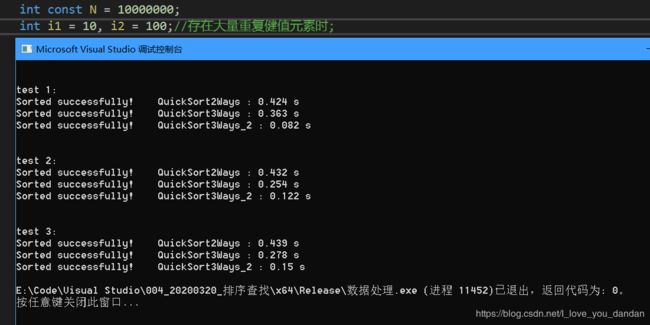
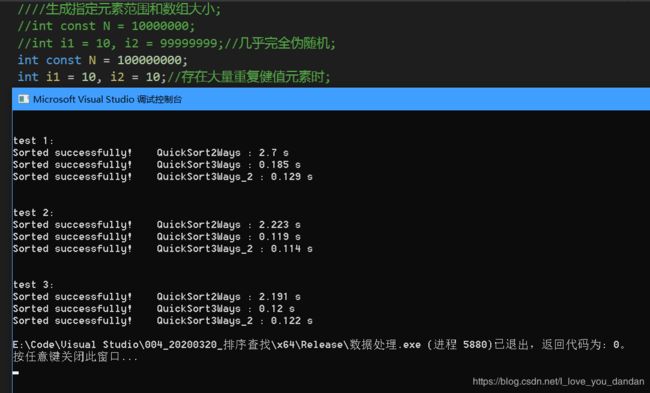
测试三:1千万数据,10万范围随机
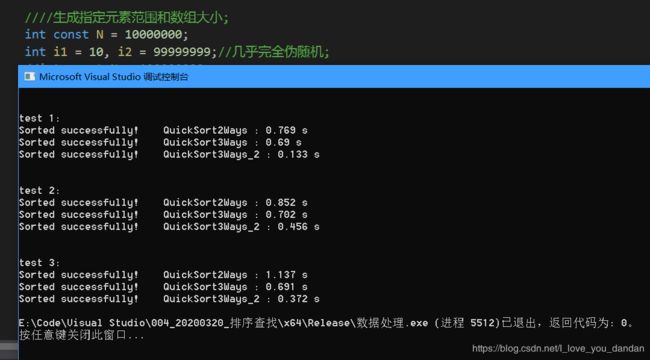
一个亿数据
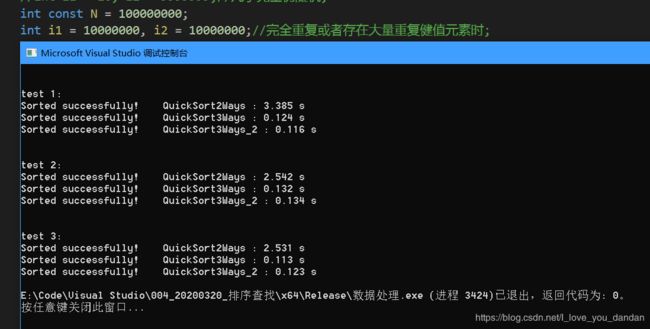
小范围随机,大量重复元素
此种情况下会存在大量的重复的元素.
由于此时单路快排的缺陷暴露无遗.
虽然三路快排擅长处理重复元素,但是性能还是不及改进后的加强型三路快排.
一千万数据
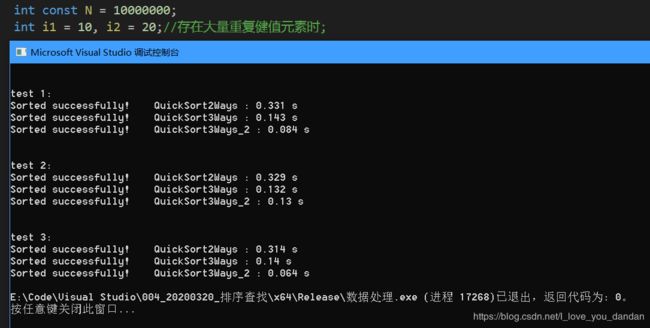
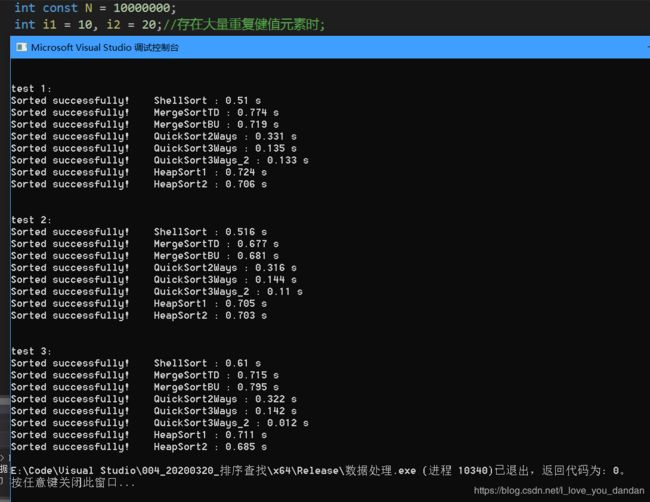
测试一:1千万数据,[10,20] 随机范围
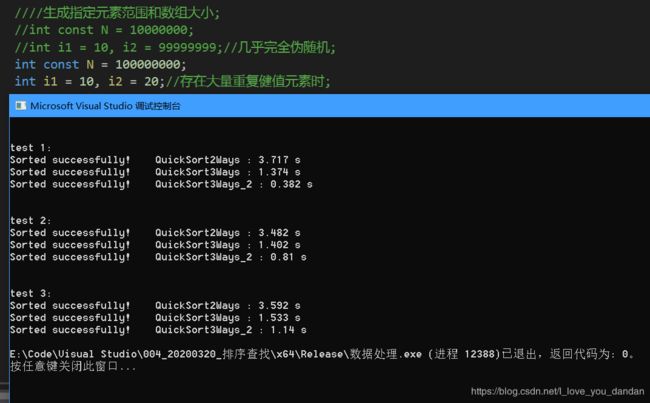
一个亿数据
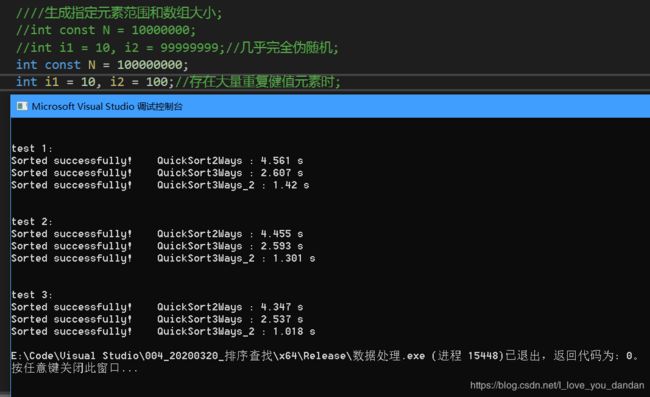
测试一:1个亿数据,[10,20] 随机范围
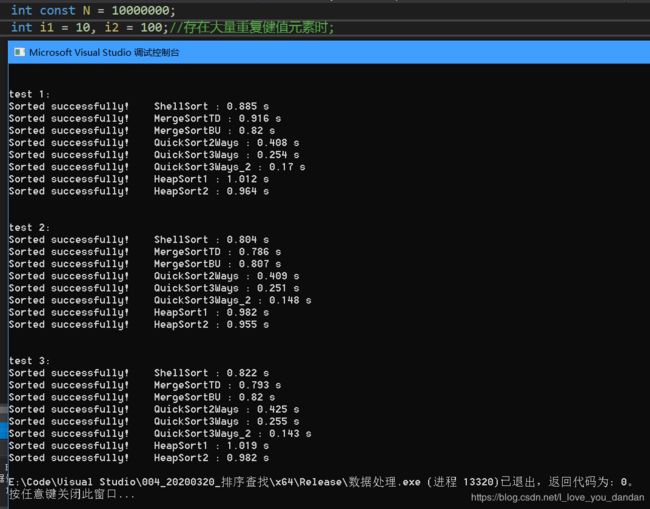
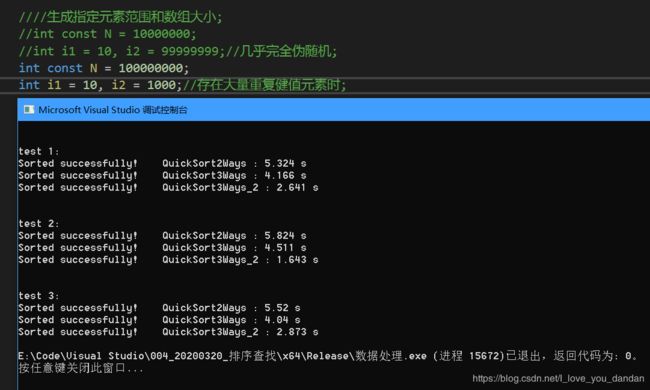
测试二:1个亿数据,[10,100] 随机范围
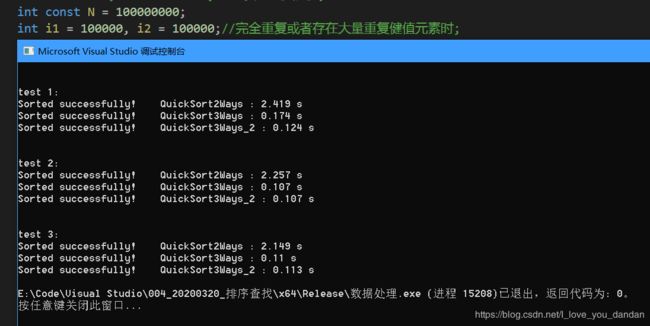
当待排序的元素完全重复时
此种情况下元素完全重复、全部相等.
由于此时单路快排退化为 O(N^2),无法参与数据测试.
理论上,处理完全重复的元素时,
改进后的加强型三路快排会退化为经典的三路快排,
并且优化操作会造成额外开销.
但是由于本设计细节的进一步改善之后,此两者算法的开销几乎相同,
甚至有时候加强型三路快排还略微快出那么一丢丢.
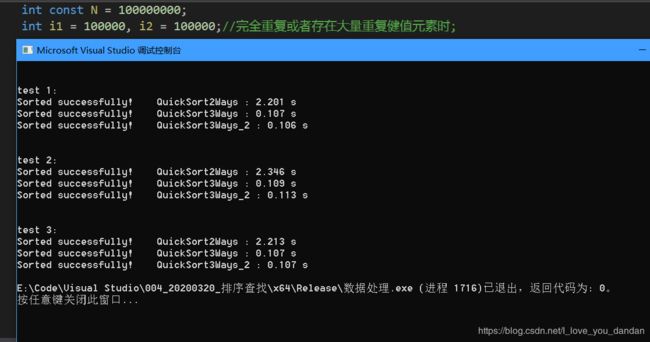
一千万数据
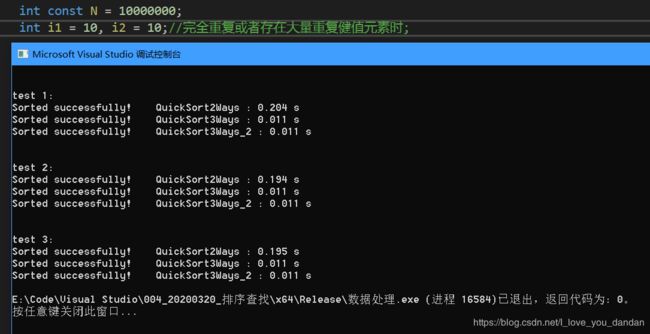
测试一:1千万数据,数值10
测试二:1千万数据,数值10000
测试三:1千万数据,数值1千万
一个亿数据
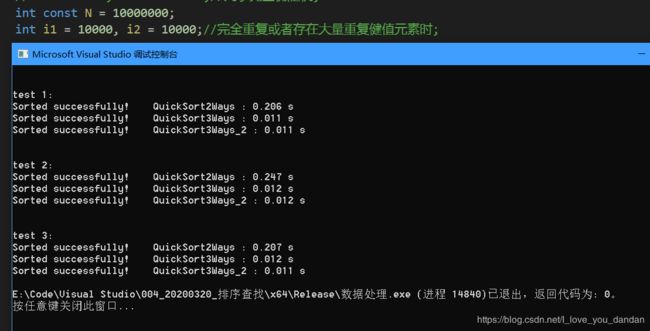
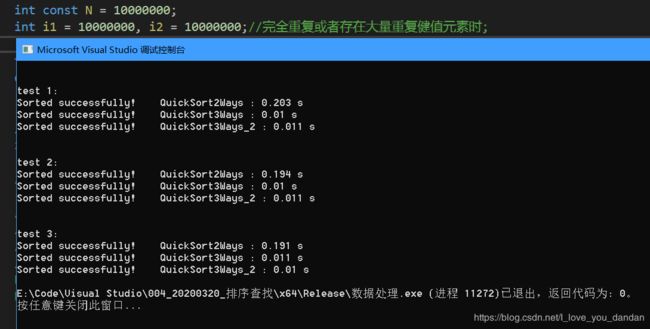
测试一:1个亿数据,数值10
测试一:1个亿数据,数值10万
测试三:1个亿数据,数值1千万
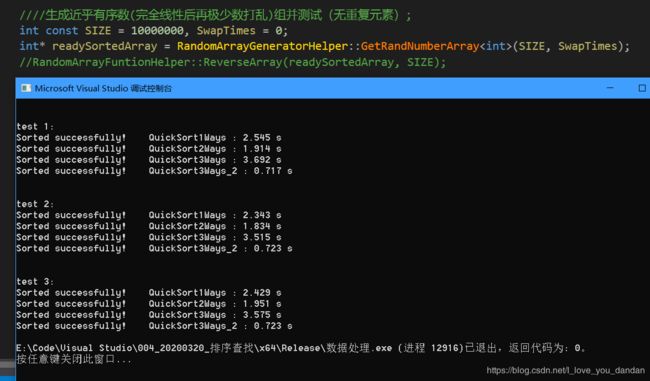
当待排序的元素线性无重时
此种情况下元素完全不重复、没有任何相等的两个元素.
此时经典的三路快排性能堪忧,因为其优化操作适得其反.
然而加强版三路快排却依旧是佼佼者.
一千万数据
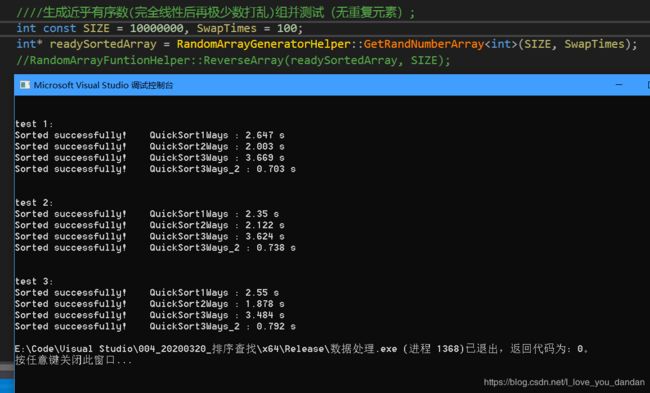
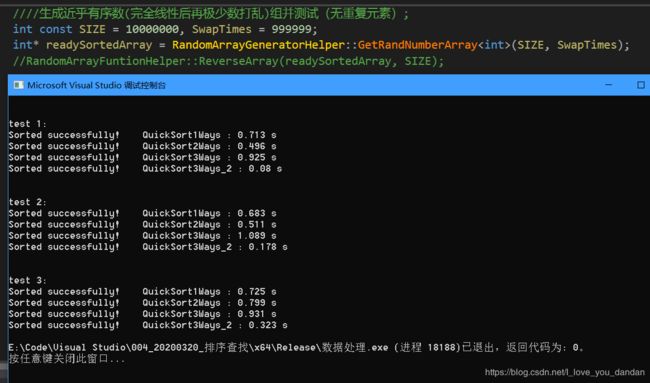
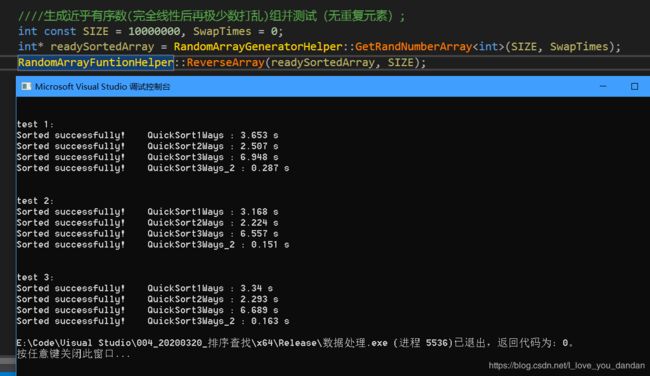
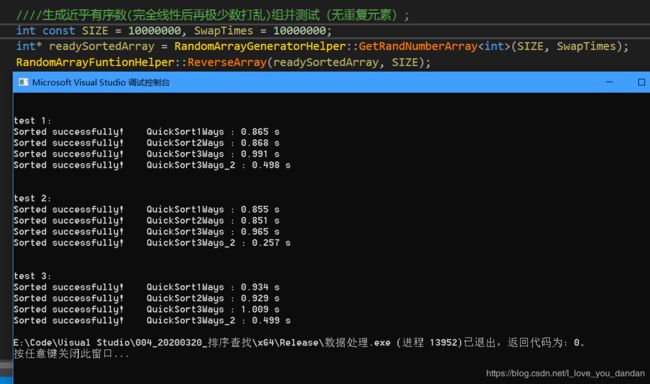
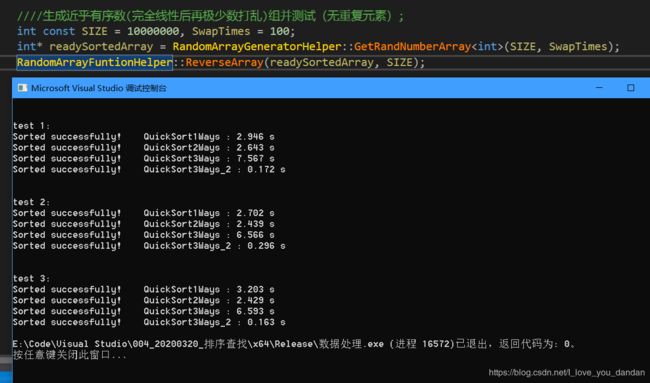
测试一:1千万数据,各个元素取对应的下标索引值,完全线性递增、顺序
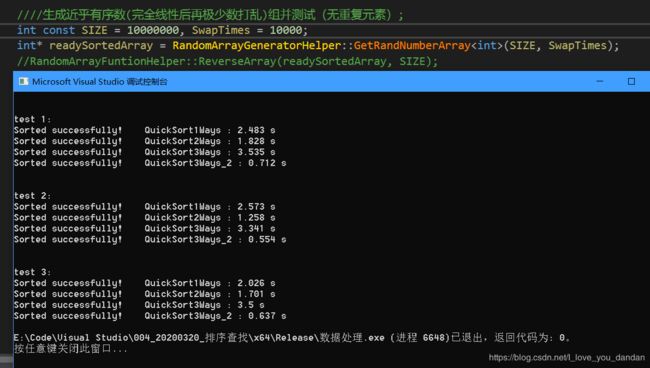
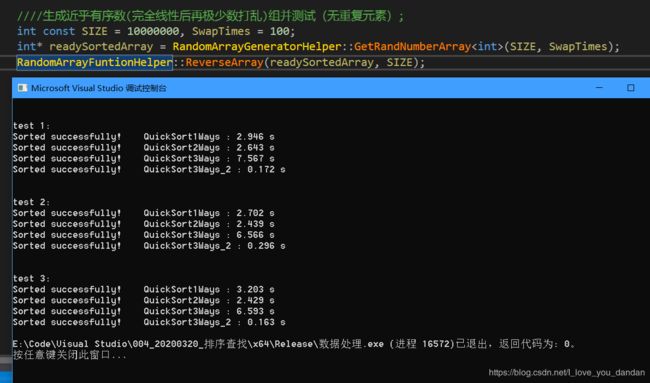
测试二:1千万数据,先完全线性递增,再进行少量元素位置交换,局部有序
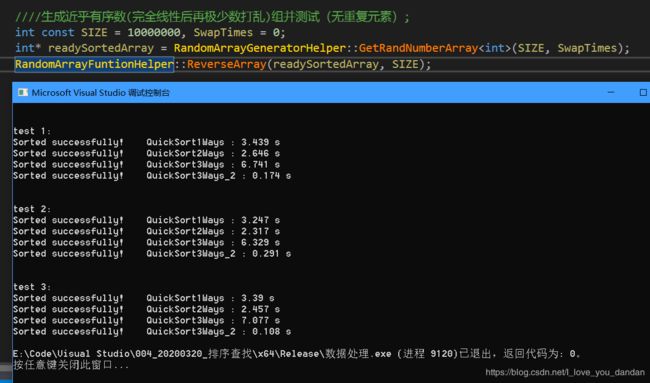
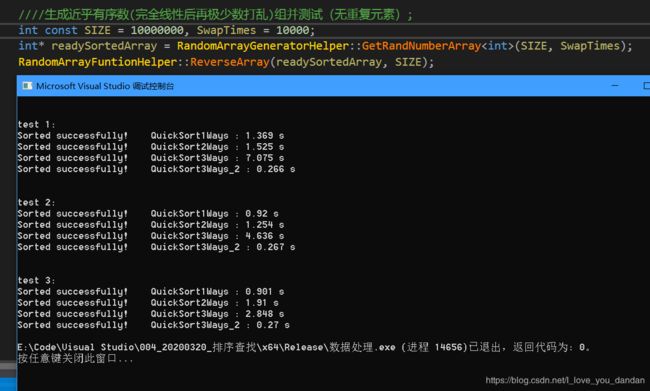
测试三:1千万数据,对上述数组元素取反后再进行排序,完全递降、逆序
测试四:1千万数据,存在大量的局部逆序对的数据
实验数据总结
无论任何类型的数据,加强型三路快排算法,
永远是四种快排设计中的最优者.
这是由自己通过不断试验和测试数据,不断改进代码的设计方式得到的.
为此,真的很欣慰!!!
通过实验发现的一些规律
规律1:线性数据、无重复元素时,数据排列越混乱,快排运行处理的效率反而越高.
这是因为快排的哨兵值划分出的区间得以更加均匀和等长化。
规律2:经典算法设计的单路快排、双路快排和三路快排,在处理局部有序的数据时,
处理大量顺序对的数据要比处理逆序对的数据更快一些(排序结果为升序).
但是加强版三路快排却与之相反,处理由大到小的降序数据要比递增的块,这应该是
由自己的设计细节决定的,即前者能够更加准确地获取最大数值 MaxNum.
规律3:完全重复的数据,其数值大小并不会对任何一种快速排序产生影响; 普适.
关于实验数据疑惑的解答
关于同一级别大小和同一数值范围的实验数据,
不同次的测试的实验结果会存在一定的出入.
为何如此?
因为自己在设计快速排序时,标定点处(即哨兵值)是随机选取的.
每一轮快排处理的区间都会随机产生一个新的哨兵数值,
故而测试结果会有一定的差异.
代码实现
由于此次三路快排的优化方式,是自己首创的.
不宜公开,:)
万分抱歉,如果让你感到不适的话.
不过,可以前来与我交流.
知识,不吝赐教!!!
不过这里可以提供一篇文章,自己就是受到这篇文章的启发进而实现了对
3路快排算法的进一步代码优化.
不胜感激!!!
文章链接:一种三路划分快速排序的改进算法
参考资料
有关快排的基本设计问题,建议看我之前的文章:
快速排序(重温经典算法系列)
快排算法排序过程的图形化演示,请参考:
排序算法过程演示
交流方式
QQ —— 2636105163(南国烂柯者)
温馨提示:
转载请注明出处!!
文章最后更新时间:
2020年3月30日05:07:14
2020年4月2日19:47:56