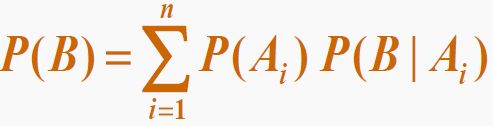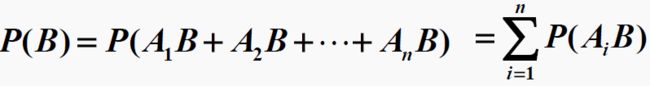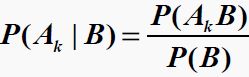Classifying with probability theory: naïve Bayes(朴素贝叶斯);classifying spam email;reveal local attitude

Naïve Bayes
Pros: Works with a small amount of data, handles multiple classes
Cons: Sensitive to how the input data is prepared
Works with: Nominal values

#1.By independence I mean statistical independence

#2. The other assumption we make is that every feature is equally important

 

Prior probability

      P(A)

for example:

There are seven possible stones and three are blue, so the probability of grabbing a blue stone: 3/7

Posterior probability（conditional probabilities）

     P(B|A)   

Given event A, then the Probabilities: P(B|A)

 

Probability Multiplication(Bayes’ rule)

     P(AB) = Pr(event A and event B)

     P(AB) = P(A) * P(B|A) = P(B) * P(A|B)   THEN   P(A|B) = P(A) * P(B|A) / P(B)          

Law of total probability

A: is a finite or countably infinite partition(In the following example, A: A1, A2,...,A8 OR box A1, box A2,...,box A8) of a sample space.

 

P(B): the probability of grabbing a blue stone(only one).

if the stones were in 8 boxes(A1,A2,...,A8), and If you wanted to calculate the probability
of drawing a blue stone from box Ai(given Ai), P(B|Ai);   and Ai is statistical independence

P(Ai and B): the probability of (grabbing from box Ai and the stone is Blue)

so the Law of total probability

 

OR

Now you know the grabbed stone is blue(Given event B), you want to know which box(A k) is it from?

for example:

if max value in the list [ P(A1|B), P(A2|B), ...,  P(An|B)] is P(A1|B), then  the blue stone are most likely from Box A1.

30%*3% + 20%*3% + 50%*1%=0.02

Document classification with naïve Bayes

A token is any combination of characters. You can think of tokens as words, but we may use things that aren’t
words such as URLs, IP addresses, or any string of characters. We’ll reduce every piece of text to a vector of tokens where 1 represents the token existing in the document and 0 represents that it isn’t present.

let’s make a quick filter for an online message board that flags a message as inappropriate if the author uses negative or abusive language. Filtering out this sort of thing is common because abusive postings make people not come back
and can hurt an online community. We’ll have two categories: abusive and not. We’ll use 1 to represent abusive and 0 to represent not abusive.

Note：

then Ai=1:abuse (class)    Ai=0: non abuse(class)

At fact， event B is also can be separeted, for instance: w1, w2, ...,wn. The above formula just for simple.

Event B　ｉｓ　ａ　ｓｅｎｔｅｎｃｅ　ｏｒ　ａ　ｄｏｃｕｍｅｎｔ:　ｗ０，　ｗ１，　ｗ２，.．．，ｗｎ　［ｎ　ｎｕｍｂｅｒｓ　ｏｆ　ｗｏｒｄｓ］

And P(B|Ai) = ( P(w0|Ai) *  P(w1|Ai) *  P(w2|Ai) * ...* P(w n-1|Ai)  )

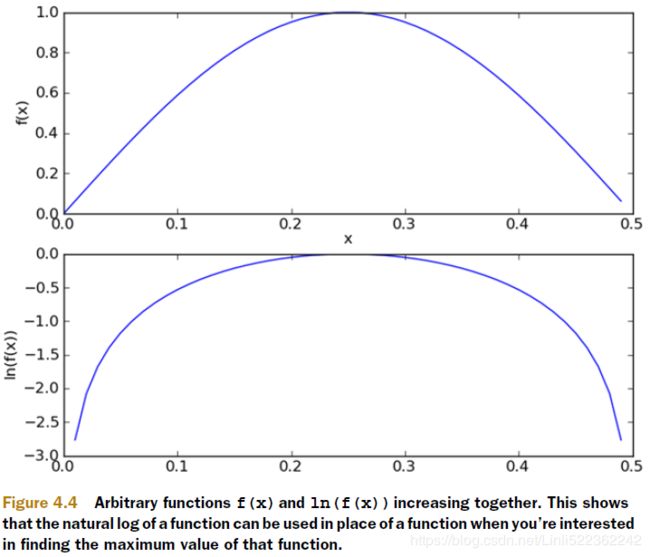
When we attempt to classify a document, we multiply a lot of probabilities together to
get the probability that a document belongs to a given class. This will look something
like p(w0|1)p(w1|1)p(w2|1). If any of these numbers are 0, then when we multiply
them together we get 0. To lessen the impact of this, we’ll initialize all of our occurrence
counts to 1, and we’ll initialize the denominators to 2．（ ｓｏｌｕｔｉｏｎ　ｃａｌｌｅｄ　additive smoothing, also called Laplace smoothing）

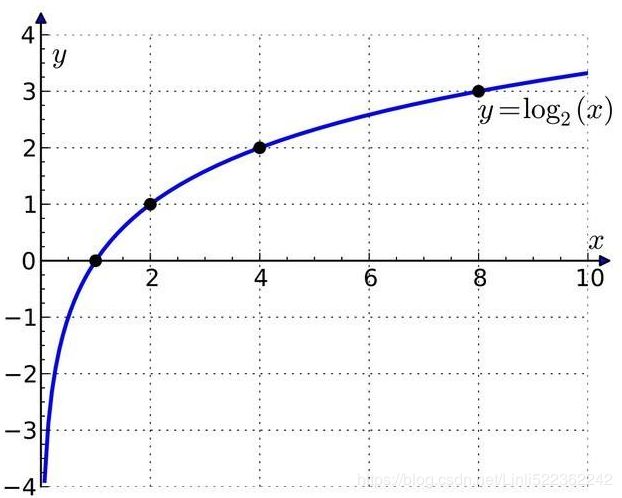
Logarithmic addition：#since the denominator may too larger and lead to the prob to 0

and but converting the large value to log value will get a negative value.

 We don't need to calculate P(B) since we can just compare the numeritor to know the result

log( P(Ai) * P(B|Ai)  )/P(B)= ( log（P(Ai) ) + log( P(B|Ai) ) )/P(B) =(  log（P(Ai) ) + log( ( P(w0|Ai) *  P(w1|Ai) *  P(w2|Ai) * ...* P(w n-1|Ai)  ) ) ) / P(B)

=log（P(Ai) ) + ( (log P(w0|Ai) +  log P(w1|Ai) + log P(w2|Ai) + ...+log P(w n-1|Ai)  ) ) / P(B)

 

# -*- coding: utf-8 -*-
"""
Created on Sun Dec  2 01:38:23 2018

@author: LlQ
"""

##############################################################################
#   Classifying with conditional probabilities(P)
#   Bayes' rule
#   P(class_i|x,y) = P(x,y|class_i) * P(class_i)) / p(x,y)
#   
#   If P(class_1|x,y) > P(class_2|x,y), the class is class_1
#   If p(class_1|x,y) < p(class_2|x,y), the class is class_2
##############################################################################

#make a quick filter
def loadDataSet():
    postingList = [
                    ['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                    ['maybe', 'not', 'take', 'him','to', 'dog','park', 'stupid'],
                    ['my', 'dalmation', 'is', 'so','cute','I', 'love', 'him'],
                    ['stop', 'posting', 'stupid', 'worthless','garbage'], 
                    ['mr', 'licks', 'ate', 'my', 'steak', 'how','to', 'stop', 'him'],
                    ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']
                 ]
    #a set of class labels                
    classList = [0,1,0,1,0,1] #1 is abusive, 0 not
    return postingList, classList

#create a vocabulary union set/list without any duplication
def createVocabList(dataSet):
    vocabSet = set([])
    for document in dataSet:
        #The | operator is used for union of two sets;
        #Bitwise OR and set union also use the same symbols 
        #in mathematical notation
        vocabSet = vocabSet | set(document)
    return list(vocabSet)

#convert a words list(inputSet) to an number list(if appear:1 ;if not: 0)
def wordSetToBinaryList(vocabList, inputSet):
    returnList = [0]*len(vocabList)  #create a list with all 0 element
    for word in inputSet:
        if word in vocabList:
            returnList[vocabList.index(word)] =1 #set to 1 if the word is in the vocablist
            
    return returnList
##############################################################################
#   import bayesMy
#   from imp import reload
#   reload(bayesMy)

#   listOfPosts, listClasses = bayesMy.loadDataSet()
#   myVocabList = bayesMy.createVocabList(listOfPosts)

#   myVocabList
#   output: ['dog','park','my','maybe','buying','has','stupid','is','to',
#            'posting','ate','food','quit','help','problems','him','licks',
#            'how','not','love','dalmation','garbage','steak','please','flea',
#            'take','so','stop','cute','I','worthless','mr']   

#   bayesMy.wordSetToBinaryList(myVocabList, listOfPosts[0])
#   output:  [1,0,1,0,0,1,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0]   
##############################################################################  
    
import numpy as np

def probsOfEachClass(trainMatrix, trainCategory):
   #trainMatrix is a matrix of documents:len(vocabularylist) x len(trainCategory)
   #trainCategory:a vector with the class labels(0|1) for each of the documents
    
   #count the number of documents in each class == rows
    numTrainDocs = len(trainMatrix) #rows=len(trainMatrix) = len(trainCategory)
    numWords = len(trainMatrix[0])  #columns of trainMatrix = len(vocabulary list)
    #two categories: 1 is abusive, 0 not
    probAbusive = sum(trainCategory)/float(numTrainDocs)#sum(1)/len(trainCategory)
                                                    #here 1/2
    
    #columns of trainMatrix == num of elements in the vocabulary list
    #prob0Num = np.zeros(numWords) #np.array
    #prob1Num = np.zeros(numWords)
    #if one of above numbers are 0, then the multiplication will be zero
    #To lessen the impact, we initialize all occurence counts to 1
    prob0Num = np.ones(numWords);
    prob1Num = np.ones(numWords);
    
    #prob0Denom=0.0#Denominator
    #prob1Denom=0.0
    #initializes the denominators to 2
    prob0Denom = 2.0;
    prob1Denom = 2.0;
    
    for i in range(numTrainDocs):#for each row of trainMatrix
        if trainCategory[i] == 1:#given class_i
            prob1Num += trainMatrix[i] #vector addition
            prob1Denom += sum(trainMatrix[i]) #horizontal sum all of w_j(1) for given class_i
            #print('prob1Num: ',prob1Num,', prob1Denom: ', prob1Denom)
        else:
            prob0Num += trainMatrix[i]
            prob0Denom += sum(trainMatrix[i])
            #print('prob0Num: ',prob0Num,', prob0Denom: ', prob0Denom)
    
    #for example: two white balls and one non_white in class_i(total 3 balls)
    #the prob(white ball/class_i) = 2/3 : p(w_j/class_i)
    #Note:  here: white=appear=1, non_white=not appear=0, total=sum Of appears         
    #p(w_j|class_i): the probility of the occurence of (w_j) in given class_i
    #p0Vect = p0Num/p0Denom 
    #change to log()
    #When we go to calculate the product p(w_0|c_0)*p(w_1|c_0)*p(w_2|c_0)...
    #many of these numbers are very small and underflow, or an incorrect answer
    prob0Vect = np.log(prob0Num/prob0Denom) #array
    #print(prob0Num)
    #print(prob0Denom)
      
    #prob1Vect = prob1Num/prob1Denom #change to log()
    prob1Vect = np.log(prob1Num/prob1Denom)
    #print(prob1Num)
    #print(prob1Denom)

    return prob0Vect, prob1Vect, probAbusive  #prob1Vect=probClass1Vect
                                              #1: Abusive                  
##############################################################################
#   import bayesMy
#   from imp import reload
#   reload(bayesMy)

#   listOfPosts, listClasses = bayesMy.loadDataSet()

#   myVocabList = bayesMy.createVocabList(listOfPosts)
    
#   trainMat=[]
#   for postList in listOfPosts:
#       trainMat.append(bayesMy.wordSetToList(myVocabList, postList))

#   for i in range(len(trainMat)):
#       print(trainMat[i])

#   output: total of even row=19   total of odd row=24
#   [1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0]
#   [1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0]
#   [0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0]
#   [0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0]
#   [0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1]
#   [1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]
    
#   listOfPosts
#   [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
#    ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
#    ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
#    ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
#    ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
#    ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    
#   prob0List, prob1List, probAbused = bayesMy.probsOfEachClass(trainMat, listClasses)
#odd    [1. 0. 3. 0. 0. 1. 0. 1. 1. 0. 1. 0. 0. 1. 1. 2. 1. 1. 0. 1. 1. 0. 1. 1. 1. 0. 1. 1. 1. 1. 0. 1.]
#odd    24.0
#even   [2. 1. 0. 1. 1. 0. 3. 0. 1. 1. 0. 1. 1. 0. 0. 1. 0. 0. 1. 0. 0. 1. 0. 0. 0. 1. 0. 1. 0. 0. 2. 0.]
#even   19.0   
 
#   probAbused
#   output: 0.5

    #1/24=0.04166667
#   prob0List: 
#   output:  array([0.04166667,           0,    0.125,...])

#   prob1List:
#   output:  array([0.10526316,  0.05263158,        0,...])  

#   myVocabList.index('cute')
#   output: 28

#   myVocabList.index('stupid')
#   output: 6

#   len(myVoCabList)
#   output: 32    
##############################################################################

def classifyNB(testBinaryVect, prob0Vect, prob1Vect, probAbusive):
    #p(w_j|c_i) need to calculate p(w_0|c_0)*p(w_1|c_0)*p(w_2|c_0)...
                                             #(log: sum of the product)
    #and   p(w_j and c_i)=p(c_i|w_j)*p(w_j) =p(w_j|c_i) * p(c_i)
                                             #(log:sum(plus) of the product)
    #convert to log by using plus and sum
    #we will compare the values of p(w_j and c_i)

    #prob1: probility is abusive class
    #prob0: probility is unabusive class
    prob1 = sum(testBinaryVect * prob1Vect) + np.log(probAbusive)
    prob0 = sum(testBinaryVect * prob0Vect) + np.log(1.0-probAbusive)
    #the resulf of sum is a log expression
    #then use the fomular: log(xy) = log(x) + log(y)
    
    if prob1>prob0:
        return 1 # abusive
    else:
        return 0 # unabusive
    
def testingNB():
    #dataSet
    listOfPosts, listOfClasses = loadDataSet()
    #using the list Of Posts to create a vocabulary list Without any repetition
    myVocabList = createVocabList(listOfPosts)
    
    trainMat = []
    for eachPostList in listOfPosts:
        #in binary list: 1 means appear in vocabulary List, 0 means not appear
        trainMat.append(wordSetToBinaryList(myVocabList, eachPostList))
    #prob0V:log( list the probility' of each word appeared in class 0 )
    #prob1V:log( list the probility' of each word appeared in class 1 )
    #converting a list to an array since np.array() has the log function
    prob0V, prob1V, probAbusive = probsOfEachClass(np.array(trainMat), \
                                                   np.array(listOfClasses))
    #test1
    testEntryList = ['love', 'my', 'dalmation']
    #converting a list to an array since np.array() has the log function    
    testEntry2BinaryList = np.array(\
                               wordSetToBinaryList(myVocabList, testEntryList))
    print(testEntryList, ' classified as: ', \
                 classifyNB(testEntry2BinaryList, prob0V, prob1V, probAbusive))
    
    #test2
    testEntryList = ['stupid', 'garbage']
    testEntry2BinaryList = np.array(\
                               wordSetToBinaryList(myVocabList, testEntryList))
    print(testEntryList, ' classified as: ', \
                 classifyNB(testEntry2BinaryList, prob0V, prob1V, probAbusive))

##############################################################################
#   import bayesMy
#   from imp import reload
#   reload(bayesMy)
    
#   bayesMy.testingNB()
#   output:
#   ['love', 'my', 'dalmation']  classified as:  0
#   ['stupid', 'garbage']  classified as:  1
##############################################################################    
 
#If a word appears more than once in a document, that might convey some sort
#of information about the document, this is called a bag-of-words model.    

#convert a words list(inputSet) to an number list(if appear: +1, if not: 0)
def bagOfWords2VecMN(vocabList, inputSet):
    returnVec = [0]*len(vocabList) #create a list with all 0 element
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] +=1
    return returnVec

#Classifying spam email with Native Bayes
import random
    #File parsing and full spam test functions
def textParse(bigString):
    import re #Regular Expression Opeartions
    listOfTokens = re.split(r'\W*', bigString) #note: case Sensitive for \w
    return[eachToken.lower() for eachToken in listOfTokens if len(eachToken)>2]

##############################################################################
#   mySent='This book is the best book on Python or M.L. I have ever laid eyes upon.'    
#   import re
#   regEx = re.compile("\\W*")
    
#   [token.lower() for token in listOfTokens if len(token) >0]
#   ['this', 'book', 'is', 'the', 'best', 'book', 'on', 'python', 'or', 'm',
#   'l', 'i', 'have', 'ever', 'laid', 'eyes', 'upon']    
##############################################################################     
def spamTest():
    docList = []; classList = []; fullText = []

    for i in range(1, 26):#there is 25 documents
        #wordList = open('email/spam/%d.txt' % i, 'r', encoding='ISO-8859-1').read()
        wordList = textParse(open('email/spam/%d.txt' % i, 'r', encoding='ISO-8859-1').read())
        #wordList = textParse(open('email/spam/%d.txt' % i, "r").read().decode('GBK','ignore') )
        docList.append(wordList)#append an element(whole wordList as an element) 
        fullText.extend(wordList)#extend a list(the word in the wordList as an element)
        classList.append(1)
        
        #wordList = open('email/ham/%d.txt' % i, 'r', encoding='ISO-8859-1').read()
        wordList = textParse(open('email/ham/%d.txt' % i, 'r', encoding='ISO-8859-1').read())
        #wordList = textParse(open('email/ham/%d.txt' % i,  "r").read().decode('GBK','ignore') )
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)
        #print(wordList)   #wordList
    
    vocabList = createVocabList(docList)   #by using set()
    #total 50(25+25) documents
    trainingSetIndex = list(range(50)) #0,1,2,..49
    
    testSetIndex=[]
    #hold-out cross validation
    for i in range(10):#randomly select 10 of those files
        randIndex = int(random.uniform(0, len(trainingSetIndex))) #0~49 less
        testSetIndex.append(trainingSetIndex[randIndex])
        del(trainingSetIndex[randIndex])
        
    trainMat=[]; trainClasses =[]
    for docIndex in trainingSetIndex:
        trainMat.append(wordSetToBinaryList(vocabList, docList[docIndex]))
        trainClasses.append(classList[docIndex])
        
    prob0Vect, prob1Vect, pSpam = probsOfEachClass(np.array(trainMat), np.array(trainClasses))
    
    errorCount = 0
    
    for docIndex in testSetIndex:
        wordList = wordSetToBinaryList(vocabList, docList[docIndex])
        if classifyNB( np.array(wordList), prob0Vect, prob1Vect, pSpam) != \
                classList[docIndex]:
            errorCount +=1
            print(" classification error", docList[docIndex])
    print('the error rate is: ', float(errorCount)/len(testSetIndex))

############################################################################## 
#   import bayesMy
#   from imp import reload
#   reload(bayesMy)
    
#   bayesMy.spamTest()
#   output:           the error rate is:  0.0    
    
#   #   bayesMy.spamTest()
#   output:
#        classification error ['oem', 'adobe', 'microsoft', 'softwares', 'fast', 
#        'order', 'and', 'download', 'microsoft', 'office', 'professional', 
#        'plus', '2007', '2010', '129', 'microsoft', 'windows', 'ultimate', 
#        '119', 'adobe', 'photoshop', 'cs5', 'extended', 'adobe', 'acrobat', 
#        'pro', 'extended', 'windows', 'professional', 'thousand', 'more', 
#        'titles']
#   the error rate is:  0.1    
############################################################################## 
    
def calcMostFreqWords(vocabList, fullText):
    import operator
    freqDict = {}
    for token in vocabList:
        freqDict[token] = fullText.count(token)#{{token:number}, {token:number}...}
        
    sortedFreq = sorted(freqDict.items(), key=operator.itemgetter(1), \
                            reverse = True)
    top30 =int(0.3*len(sortedFreq))
    return sortedFreq[:top30]#to get top 30% words

def stopWords():
    import re
    wordList = open('stopword.txt').read()
    listOfTokens = re.split(r'\W*', wordList)
    return [tok.lower() for tok in listOfTokens]

#holdout method: 20% for testSet, 80% for training set
    #the part is similar to spamTest()
def localWords(feed1, feed0):
    #import feedparser
    docList = []; classList=[]; fullText=[]
    minLen = min(len(feed1['entries']), len(feed0['entries']))
    
    for i in range(minLen):
        wordList = textParse(feed1['entries'][i]['summary'])
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(1)
        
        wordList = textParse(feed0['entries'][i]['summary'])
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)
        
    vocabList = createVocabList(docList)
    
    #########################################################################
     #top30Words = calcMostFreq(vocabList, fullText) #top 30% of the words
     #top30Words: {{word:number}, {word:number}...}
        #remove top 30 words from vocabList
    #for pairW in top30Words:
    #    if pairW[0] in vocabList: #pairW[0] is the key in dict
    #        vocabList.remove(pairW[0])
    #########################################################################
    
    #since I don't have enough data, so I use stopWords()
    stopWordList = stopWords()
    for stopWord in stopWordList:
        if stopWord in vocabList:
            vocabList.remove(stopWord)
            
    #trainingSetIndex = list(range(2*minLen)); testSetIndex=[]
    #since I don't have enough data
    trainingSetIndex = list(range(minLen)) #0,1,2,3 ... minLen-1
    testSetIndex = []
    
    #hold-out
    percentage = int(0.2*len(trainingSetIndex))
    for i in range(percentage):
        randIndex = int(random.uniform(0, len(trainingSetIndex)))
        testSetIndex.append(trainingSetIndex[randIndex])
        del(trainingSetIndex[randIndex])
    
    trainingSetMat=[]
    trainingClasses = []
    for docIndex in trainingSetIndex:
        trainingSetMat.append(bagOfWords2VecMN(vocabList, docList[docIndex]))
        trainingClasses.append(classList[docIndex])
     
    prob0V, prob1V, pSpam= probsOfEachClass(np.array(trainingSetMat), np.array(trainingClasses))
    
    errorCount=0
    for docIndex in testSetIndex:
        wordVector = bagOfWords2VecMN(vocabList, docList[docIndex])
        if classifyNB(np.array(wordVector), prob0V, prob1V, pSpam) != \
                        classList[docIndex]:
           errorCount +=1
    print('the error rate is:', float(errorCount)/len(testSetIndex))
    return vocabList, prob0V, prob1V
    
##############################################################################     
#   import bayesMy
#   from imp import reload
#   reload(bayesMy)
#   import feedparser        
 
#   ny = feedparser.parse('http://www.nasa.gov/rss/dyn/image_of_the_day.rss')
#   len(ny['entries'])
#   60

#   sf = feedparser.parse('http://rss.yule.sohu.com/rss/yuletoutiao.xml')
#   len(sf['entries'])
#   30

#   vocabList, probSF, probNY = bayesMy.localWords(ny, sf)
#   the error rate is: 0.5

#   vocabList, probSF, probNY = bayesMy.localWords(ny, sf)
#   the error rate is: 0.6666666666666666 
    
#   vocabList, probSF, probNY = bayesMy.localWords(ny, sf)
#   the error rate is: 0.8333333333333334
    
#   vocabList, probSF, probNY = bayesMy.localWords(ny, sf)
#   the error rate is: 0.16666666666666666
    
#To get a good estimate of the error rate, you should do multiple trials of 
#this and take the average. The error rate here is much higher than for the 
#spam testing. That is not a huge problem because we’re interested in the word 
#probabilities, not actually classifying anything. You can play around the 
#number of words removed by caclMostFreq() and see how the error rate changes.
    
#You can comment out the three lines that removed the most frequently used words
#and see that an error rate of 54% without these lines and 70% with the lines 
#included. An interesting observation is that the top 30 words in these posts 
#make up close to 30% of all the words used. The size of the vocabList was ~3000 
#words when I was testing this. 
#A small percentage of the total words makes up 
#a large portion of the text. The reason for this is that a large percentage
#of language is redundancy and structural glue.
############################################################################## 
    
def getTopWords(ny, sf):
    vocabList, prob0V, prob1V = localWords(ny,sf)
    topNY = []
    topSF = []
    for i in range(len(prob0V)):
        if prob0V[i] > -6.0 :
            topSF.append((vocabList[i], prob0V[i])) #tuple
        
        if prob1V[i] > -6.0 :
            topSF.append((vocabList[i], prob1V[i]))
            
                                        #prob1V[i]    
    sortedSF = sorted(topSF, key=lambda pair:pair[1], reverse=True)
    print("SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**")
    for item in sortedSF:
        print(item[0])#word
    
    sortedNY = sorted(topNY, key=lambda pair:pair[1], reverse=True)
    print ("NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**")
    
    for item in sortedNY:
        print(item[0])
        
##############################################################################
#   import bayesMy
#   from imp import reload
#   reload(bayesMy)    
        
#   ny = feedparser.parse('http://www.nasa.gov/rss/dyn/image_of_the_day.rss')
#   sf = feedparser.parse('http://rss.yule.sohu.com/rss/yuletoutiao.xml')

#   bayesMy.getTopWords(ny,sf)
#   output:
#   the error rate is: 0.6666666666666666
#   SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**
#   搜狐娱乐讯
#   160
#   space
#   择天记
#   cygnus
#   nasa
#   northrop
#   astronaut
#   spacecraft
#   grumman
#   的开播可谓是声势浩大
#   方媛在instagram秒删的两张图片
#   NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY** 
        
#   Using probabilities can sometimes be more effective than using hard rules 
#   for classification. Bayesian probability and Bayes’ rule gives us a way to 
#   estimate unknown probabilities from known values.  
#           
#   The assumption we make is that the probability of one word doesn’t depend 
#   on any other words in the document. We know this assumption is a little 
#   simple. That’s why it’s known as naïve Bayes. Despite its incorrect
#   assumptions, naïve Bayes is effective at classification.

#   The bag-of-words model is an improvement on the set-of-words model when 
#   approaching document classification. There are a number of other improvements, 
#   such as removing stop words, and you can spend a long time optimizing a tokenizer        
##############################################################################