Python-量化投资（二）

投资组合的收益与风险

投资组合的收益率为Rp为：

import numpy as np
import math
import matplotlib.pyplot as plt
def cal_mean(frac):
    return(0.08*frac+0.15*(1-frac))

mean=list(map(cal_mean,[x/50 for x in range(51)]))
sd_mat=np.array([list(map(lambda x: math.sqrt((x**2)*0.12**2+
((1-x)**2)*0.25**2+2*x*(1-x)*(-1.5+i*0.5)*0.12*0.25),[x/50 for x in range(51)])
) for i in range(1,6)])
#[expression for variable in sequence] list comprehension
plt.plot(sd_mat[0,:],mean,label='-1')
plt.plot(sd_mat[1,:],mean,label='-0.5')
plt.plot(sd_mat[2,:],mean,label='0')
plt.plot(sd_mat[3,:],mean,label='0.5')
plt.plot(sd_mat[4,:],mean,label='1')
plt.legend(loc='upper left')

Markowitz均值-方差模型

利用Markowitz模型进行数量化的资产配置，用Python实现

股票代码	股票名称
600004	白云机场
600015	华夏银行
600023	浙能电力
600033	福建高速
600183	生益科技

import pandas as pd
stock=pd.read_table('stock.txt',sep='\t',index_col='Trddt')
stock.index=pd.to_datetime(stock.index)
fjgs = stock.loc[stock.Stkcd==600033,"Dretwd"]
fjgs.name="fjgs"
zndl=stock.loc[stock.Stkcd==600023,'Dretwd']
zndl.name='zndl'
sykj=stock.loc[stock.Stkcd==600183,'Dretwd']
sykj.name='sykj'
hxyh=stock.loc[stock.Stkcd==600015,'Dretwd']
hxyh.name='hxyh'
byjc=stock.loc[stock.Stkcd==600004,'Dretwd']
byjc.name='byjc'
sh_return = pd.concat([fjgs,zndl,sykj,kxyh,byjc],axis=1)
sh_return.head()

• 查看各股的回报率

sh_return=sh_return.dropna()
sh_return.corr()  #删除nan，以及空缺的
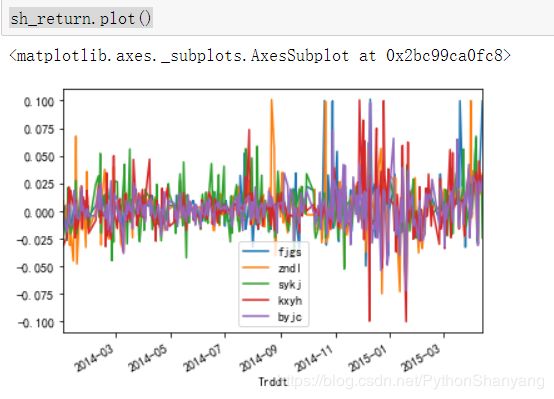
sh_return.plot()

• 查看各股的累计收益

cumreturn= (1+sh_return).cumprod()  #(1+sh_return)  +1 表示加上本身
cumreturn.plot()  #累计收益

• 查看各股回报率的相关性

sh_return.corr()

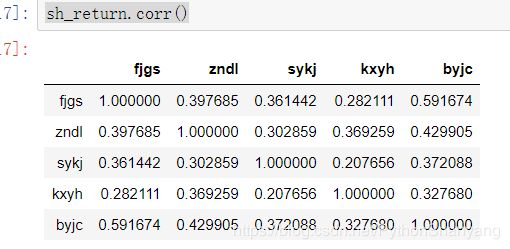
从相关系数矩阵可以看出，5只股票之间都是正向相关的。若股票之间的相关性太高，投资组合降低风险的效果就比较有限。

绘制最小方差前缘曲线

借助Python构建一个MeanVariance类，该类可以根据输入的收益率序列，求解二次规划问题，计算出最优资产比例，并绘制最小方差前缘曲线。

import ffn
from scipy import linalg
class MeanVariance:
    #定义构造器，传入收益率数据
    def __init__(self,returns):
        self.returns=returns
    #定义最小化方差的函数，即求解二次规划
    def minVar(self,goalRet):
        covs=np.array(self.returns.cov())
        means=np.array(self.returns.mean())
        L1=np.append(np.append(covs.swapaxes(0,1),[means],0),
                     [np.ones(len(means))],0).swapaxes(0,1)
        L2=list(np.ones(len(means)))
        L2.extend([0,0])
        L3=list(means)
        L3.extend([0,0])
        L4=np.array([L2,L3])
        L=np.append(L1,L4,0)
        results=linalg.solve(L,np.append(np.zeros(len(means)),[1,goalRet],0))
        return(np.array([list(self.returns.columns),results[:-2]]))
    #定义绘制最小方差前缘曲线函数
    def frontierCurve(self):
        goals=[x/500000 for x in range(-100,4000)]
        variances=list(map(lambda x: self.calVar(self.minVar(x)[1,:].astype(np.float)),goals))
        plt.plot(variances,goals)
    #给定各资产的比例，计算收益率均值  
    def meanRet(self,fracs):#fracs 概率
        meanRisky=ffn.to_returns(self.returns).mean()
        assert len(meanRisky)==len(fracs), 'Length of fractions must be equal to number of assets'
        return(np.sum(np.multiply(meanRisky,np.array(fracs))))
    #给定各资产的比例，计算收益率方差
    def calVar(self,fracs):
        return(np.dot(np.dot(fracs,self.returns.cov()),fracs))

• 绘制最小方差前缘曲线

minvar=MeanVariance(sh_return)
minvar.frontierCurve() #收益方差最低点

• 假设目标期望收益率（日期期望收益率）是0.003，然后将整个数据集分为训练集和测试集，用训练集的数据来得到最优资产配置，用测试集来看资产配置是否有效。

#选取训练集和测试集
train_set=sh_return["2014"]
test_set=sh_return["2015"]#训练数据，分别导入2014，2015
#选取组合
varMinmize = MeanVariance(train_set)
goal_return = 0.003
profolio_weight = varMinmize.minVar(goal_return)  #计算最小方差
profolio_weight 
'''
profolio_weight 权重，五种股票的比例权重
array([['fjgs', 'zndl', 'sykj', 'kxyh', 'byjc'],
       ['0.8121632841002377', '-0.4801112026506777',
        '0.43018219629259896', '0.34747305363072123',
        '-0.10970733137288022']], dtype='
#

#计算测试集的收益率

#计算测试集的收益率
test_return=np.dot(test_set,np.array([profolio_weight[1,:].astype(np.float)]).swapaxes(0,1))
test_return=pd.DataFrame(test_return,index=test_set.index)
test_cum_return = (1+test_return).cumprod()#累计收益
plt.plot(test_cum_return.index,test_cum_return)

#与随机生成的组合进行比较

sim_weight=np.random.uniform(0,1,(100,5))
#叠加
sim_weight=np.apply_along_axis(lambda x: x/sum(x),1,sim_weight)#随机数
sim_return=np.dot(test_set,sim_weight.swapaxes(0,1))
sim_return=pd.DataFrame(sim_return,index=test_cum_return.index)
sim_cum_return=(1+sim_return).cumprod()
plt.plot(sim_return.index,sim_cum_return)
plt.plot(test_cum_return.index,test_cum_return,color="yellow")

Black-Litterman模型（BL模型）

不同于Markowitz模型对于得到的最优资产配置比对输入过于敏感。

• P和Q的计算公式：
  
  大概推算是：
  P看好为正，不看好为负
  q就是比较收益率的数组
• 定义函数

def blacklitterman(returns,tau, P, Q):
  mu=returns.mean()
  sigma=returns.cov()
  pi1=mu
  ts = tau * sigma
  Omega = np.dot(np.dot(P,ts),P.T) * np.eye(Q.shape[0])
  middle = linalg.inv(np.dot(np.dot(P,ts),P.T) + Omega)  
  er = np.expand_dims(pi1,axis=0).T + np.dot(np.dot(np.dot(ts,P.T),middle),
                      (Q - np.expand_dims(np.dot(P,pi1.T),axis=1)))
  posteriorSigma = sigma + ts - np.dot(ts.dot(P.T).dot(middle).dot(P),ts)
  return [er, posteriorSigma]

• 条件1的P和Q

pick1=np.array([1,0,1,1,1])
q1 = np.array([0.003*4])

• 条件2的P和Q

pick2=np.array([0.5,0.5,0,0,-1])
q2 = np.array([0.001])

• P和Q

P=np.array([pick1,pick2])
Q=np.array([q1,q2])

• 修正后验收收益

res=blacklitterman(sh_return,0.1, P, Q)
p_mean=pd.DataFrame(res[0],index=sh_return.columns,columns=['posterior_mean'])
p_mean

p_cov=res[1]
p_cov

• 计算权重

def blminVar(blres,goalRet):
        #covs=np.array(blres[1])
        #means=np.array(blres[0])
		covs = np.array(blres[1],dtype=float)
		means = np.array(blres[0],dtype=float)
        L1=np.append(np.append((covs.swapaxes(0,1)),[means.flatten()],0),
                               [np.ones(len(means))],0).swapaxes(0,1)
        L2=list(np.ones(len(means)))
        L2.extend([0,0])
        L3=list(means)
        L3.extend([0,0])
        L4=np.array([L2,L3])
        L=np.append(L1,L4,0)
        results=linalg.solve(L,np.append(np.zeros(len(means)),[1,goalRet],0))
        return(pd.DataFrame(results[:-2],
                            index=blres[1].columns,columns=['p_weight']))

• 结合投资人观点的资产后验分布结果res以及投资人目标收益率（年收益率为75%）作为blminVar()函数的输入变量，可得最优资产配置比

blresult = blminVar(res,0.75/252)
print(blresult)