【动态规划】LCS算法 python

问题描述1

求两字符串的连续最大公共子字符串(The Longest Common Substring)
这个LCS问题就是求两个字符串最长公共子串的问题。解法就是用一个矩阵来记录两个字符串中所有位置的两个字符之间的匹配情况，若是匹配则为1,否则为0。然后求出对角线最长的1的序列，其对应的位置就是最长匹配子串的位置。如图1所示，在对角线上，连续的1就代表了两字符串对应的位置连续相等。

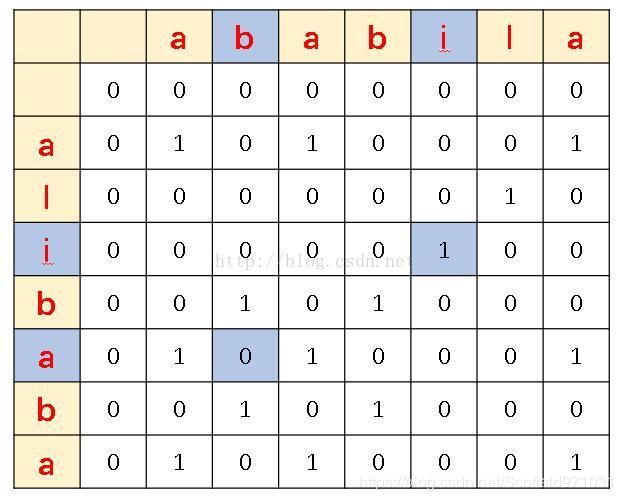
从该矩阵中找到最长的全为1的对角线，就可以找到最大公共子串，分别找出对应的字符即可求出这个最长子串。如图1，有两个最长的公共子串，bab与aba。

综上所述，基本思路分为两步：

1. 算一个匹配矩阵存放两个字符串每个字符之间的匹配情况，相同为1，不同为0。
2. 求这个矩阵中连续的最长的值为1的对角线，得到这个对角线之后我们就得到了公共子串的长度和位置（行列索引值）

改进算法

求出字符串匹配矩阵是很简单的事情，但是当我们得到0/1矩阵时，我们要怎么去找到最长的对角线呢？这是一个比较麻烦的问题。

我们可以对这个算法进行改进，即在填充这个矩阵的值的时候，不仅仅是0和1，而是把公共子串的最大长度的值填入相应的位置。我们的目的很清楚，就是在图1的基础上把最长的对角线的值改为1.2.3…，代表了公共子串的长度，看下面两个图会比较清楚：


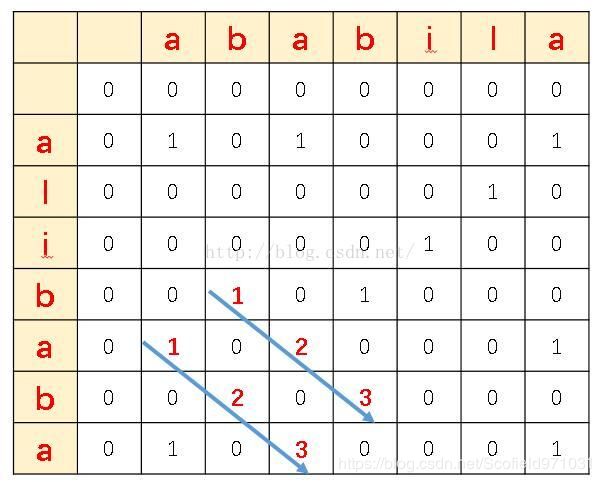
我们想一下，把矩阵变成这样之后，每个元素的值m[i][j]代表的是子串s1的前i部分和子串s2的前j部分中最大公共子串的长度。那么其实这个矩阵中最大的元素的值就代表了公共子串的最大长度，而且通过这个最大元素的行列索引我们就可以定位到这个公共子串在原字符串中的结束位置，再通过长度就可以反推出公共子串的内容了。下面我们讲一下代码思路：

思路：当两个字符串中找到匹配的字符之后，s1[i]=s2[j]，那么我们要填入矩阵[i,j]位置的值取决于它的左上方的值，填入的值为左上方的值+1，代表这个字符可以加入现有的公共子串。

代码

def find_lcsubstr(s1, s2):
    m = [[0 for i in range(len(s2) + 1)] for j in range(len(s1) + 1)]  # 生成0矩阵，为方便后续计算，比字符串长度多了一列
    mmax = 0  # 最长匹配的长度
    p = 0  # 最长匹配对应在s1中的最后一位
    for i in range(len(s1)):
        for j in range(len(s2)):
            if s1[i] == s2[j]: # 如果相等，则加入现有的公共子串
                m[i + 1][j + 1] = m[i][j] + 1
                if m[i + 1][j + 1] > mmax:
                    mmax = m[i + 1][j + 1]
                    p = i + 1
    return s1[p - mmax:p], mmax  # 返回最长子串及其长度

问题描述2

求两个字符串的最大公共子序列（LCS）（序列可以不连续）
子串要求字符必须是连续的，但是子序列就不是这样。最长公共子序列是一个十分实用的问题，它可以描述两段文字之间的“相似度”，即它们的雷同程度，从而能够用来辨别抄袭。对一段文字进行修改之后，计算改动前后文字的最长公共子序列，将除此子序列外的部分提取出来，这种方法判断修改的部分，往往十分准确。

例如：alibaba和ababila的最大公共子序列为ababa

算法思路

思路：还是使用一个匹配矩阵来存放相关信息。此时矩阵的元素代表字符串s1前i个字符与字符串s2前j个字符的最大公共子序列长度。那么如何填充这个矩阵呢？
对于字符串a和字符串b，长度分别为m,n，先考虑他们的最后一个字符。

1. 如果相等，说明这个字符一定可以成为最大公共子序列的最后一个字符，那么我们就可以不管这个字符，去求a[0:m-1] 和 b[0:n-1]的最大公共子序列。
   对于矩阵来说，这个关系就是：如果s1[i] = s2[j]，那么m[i][j] = m[i-1][j-1] + 1
   图中就表示为斜对角左上方的值加1
2. 如果不等，那么就变成去求a[0:m-1]和b[0:n]（丢弃a的最后一位） 或者a[0:m]和 b[0:n-1]（丢弃b的最后一位）的最大公共子序列
   对于矩阵来说，关系是：m[i][j] = MAX{m[i-1][j], m[i][j-1]}
   图中就表示为是上方的值和左方的值中取大的那个

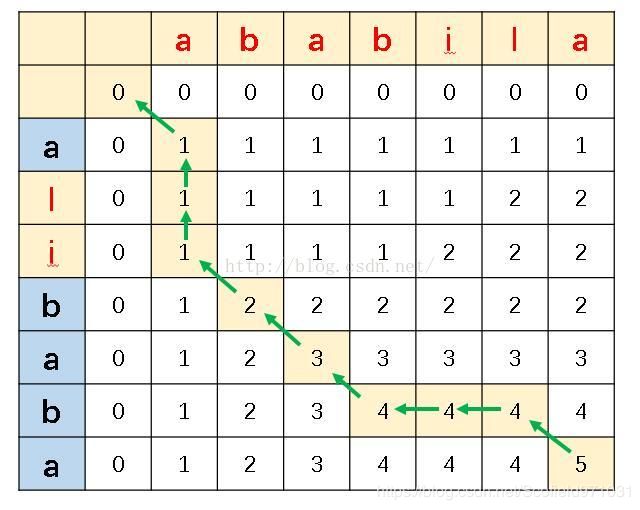
例如：图2中红色的2：判断行列字符都是b，因此为左上角1+1得到2；图2中绿色的3：判断行列字符b和a不等，取上方和左方的最大值3.

整个矩阵求出之后，右下角的元素值就是字符串a和b的最大公共子序列的长度了。

根据上文的推到思路可以找到回溯思路，从右下角开始
（1）如果当前元素等于其左上角加1，那么当前元素行列相等，是公共子序列中的一个，保存下来。
（2）如果当前元素来自上方或左方，当前元素不保存。

按照此思路，从5开始，形成如图所示的回溯路线，只有斜向上的箭头对应的行元素纳入最大公共子序列，求得最大公共子序列为ababa。

代码

一个矩阵记录两个字符串中匹配情况，若是匹配则为左上方的值加1，否则为左方和上方的最大值。一个矩阵记录转移方向，然后根据转移方向，回溯找到最长子序列。

def find_lcseque(s1, s2):
    # 生成字符串长度加1的0矩阵，m用来保存对应位置匹配的结果
    m = [[0 for x in range(len(s2) + 1)] for y in range(len(s1) + 1)]
    # d用来记录转移方向
    d = [[None for x in range(len(s2) + 1)] for y in range(len(s1) + 1)]

    for p1 in range(len(s1)):
        for p2 in range(len(s2)):
            if s1[p1] == s2[p2]:  # 字符匹配成功，则该位置的值为左上方的值加1
                m[p1 + 1][p2 + 1] = m[p1][p2] + 1
                d[p1 + 1][p2 + 1] = 'ok'
            elif m[p1 + 1][p2] > m[p1][p2 + 1]:  # 左值大于上值，则该位置的值为左值，并标记回溯时的方向
                m[p1 + 1][p2 + 1] = m[p1 + 1][p2]
                d[p1 + 1][p2 + 1] = 'left'
            else:  # 上值大于左值，则该位置的值为上值，并标记方向up
                m[p1 + 1][p2 + 1] = m[p1][p2 + 1]
                d[p1 + 1][p2 + 1] = 'up'
    (p1, p2) = (len(s1), len(s2))
    print(numpy.array(d))
    s = []
    while m[p1][p2]:  # 不为None时
        c = d[p1][p2]
        if c == 'ok':  # 匹配成功，插入该字符，并向左上角找下一个
            s.append(s1[p1 - 1])
            p1 -= 1
            p2 -= 1
        if c == 'left':  # 根据标记，向左找下一个
            p2 -= 1
        if c == 'up':  # 根据标记，向上找下一个
            p1 -= 1
    s.reverse()
    return ''.join(s)

if __name__ == '__main__':
    print(find_lcseque( 'alibaba','ababila'))

对这个回溯矩阵比划一下可以发现跟上面画的图一模一样

最后附上参考的博客并表示感谢：
https://blog.csdn.net/wateryouyo/article/details/50917812
https://blog.csdn.net/yebanxin/article/details/52190683
https://blog.csdn.net/yebanxin/article/details/52186706