Weirenren_027

极大极小值算法

极小极大的定义
Minimax算法 又名极小化极大算法，是一种找出失败的最大可能性中的最小值的算法（即最小化对手的最大得益）。通常以递归形式来实现。

Minimax算法常用于棋类等由两方较量的游戏和程序。该算法是一个零总和算法，即一方要在可选的选项中选择将其优势最大化的选择，另一方则选择令对手优势最小化的一个，其输赢的总和为0（有点像能量守恒，就像本身两个玩家都有1点，最后输家要将他的1点给赢家，但整体上还是总共有2点）。很多棋类游戏可以采取此算法，例如tic-tac-toe。

关于极小极大，更多的信息可参考以下文章：

Minimax(wikipedia)

Understanding The MiniMax Algorithm

Minimax Explained

最小最大原理与搜索方法

以TIC-TAC-TOE为例

tic-tac-toe就是我们小时候玩的井字棋（我这边习惯叫“井字过三关”），不熟悉的可以参考wiki 。

一般X的玩家先下。设定X玩家的最大利益为正无穷（+∞），O玩家的最大利益为负无穷（-∞），这样我们称X玩家为MAX（因为他总是追求更大的值），成O玩家为MIN（她总是追求更小的值），各自都为争取自己的最大获益而努力。

现在，让我们站在MAX的立场来分析局势（这是必须的，应为你总不能两边倒吧，你喜欢的话也可以选择MIN）。由于MAX是先下的（习惯上X的玩家先下），于是构建出来的博弈树如下(前面两层)：

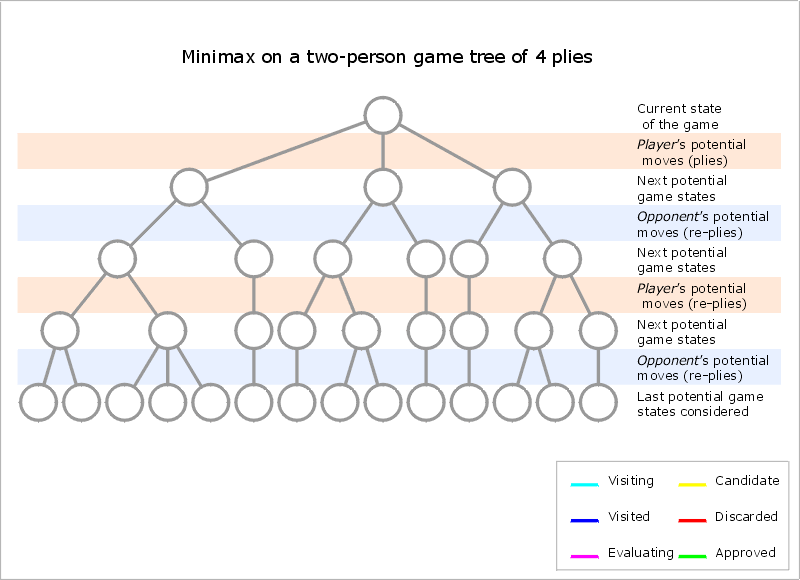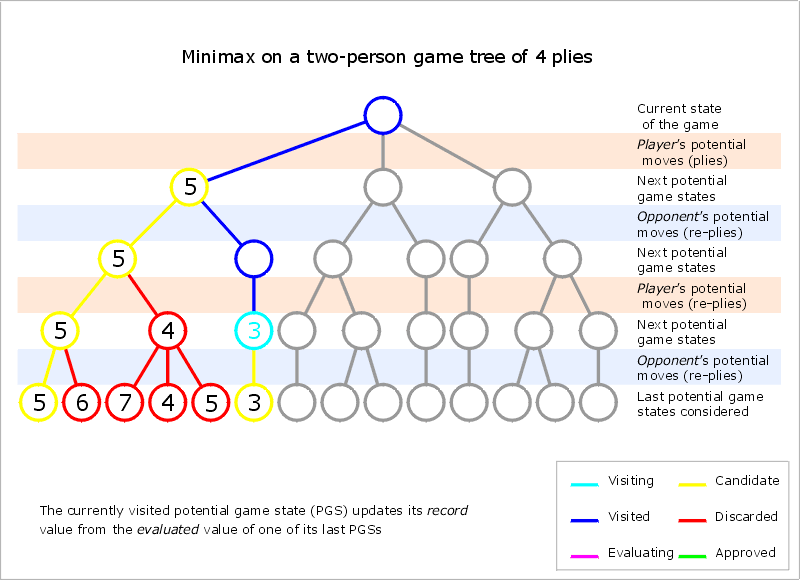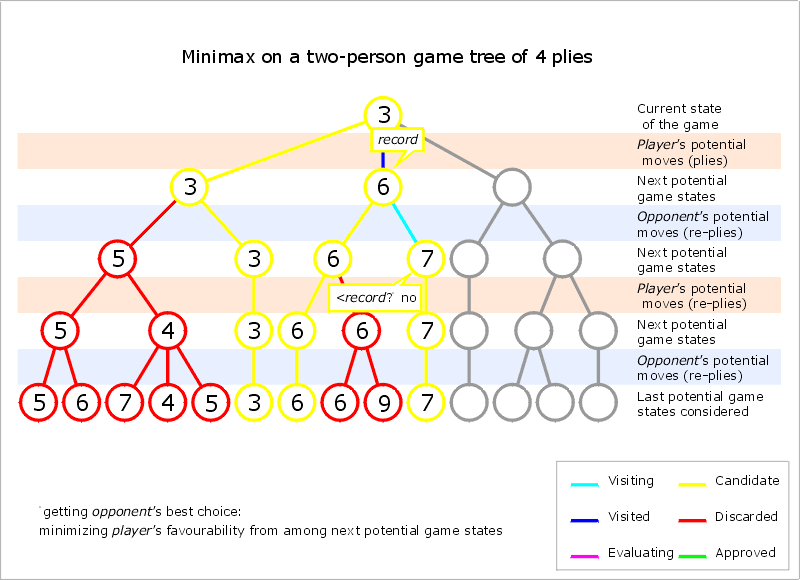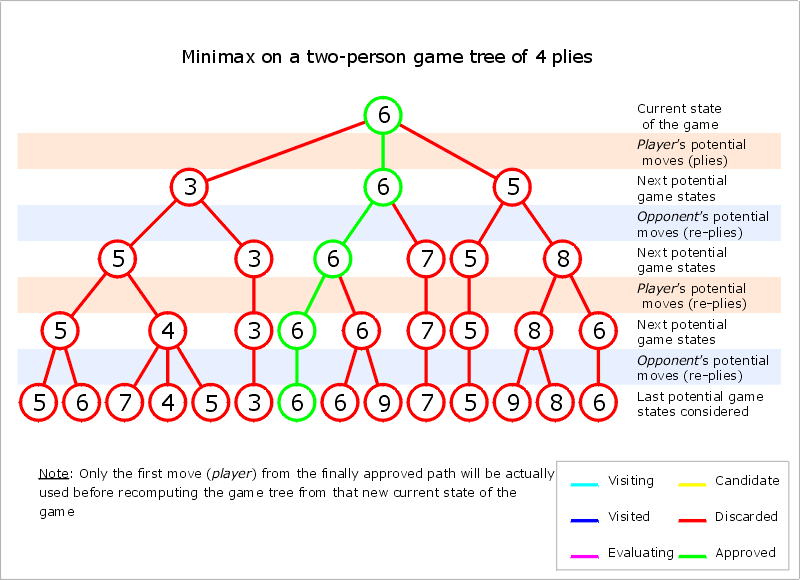
MAX总是会选择MIN最大获利中的最小值（对MAX最有利），同样MIN也会一样，选择对自己最有利的（即MAX有可能获得的最大值）。有点难理解，其实就是自己得不到也不给你得到这样的意思啦，抢先把对对手有利的位置抢占了。你会看出，这是不断往下深钻的，直到最底层（即叶节点）你才能网上回溯，确定那个是对你最有利的。
具体过程会像是这么一个样子的：

但实际情况下，完全遍历一颗博弈树是不现实的，因为层级的节点数是指数级递增的：

层数节点数

0 1

1 9

2 72

3 504

4 3024

5 15120

6 60480

7 181440

8 362880

完全遍历会很耗时...一般情况下需要限制深钻的层数，在达到限定的层数时就返回一个估算值（通过一个启发式的函数对当前博弈位置进行估值），这样获得的值就不是精确的了（遍历的层数越深越精确，当然和估算函数也有一定关系），但该值依然是足够帮助我们做出决策的。于是，对耗时和精确度需要做一个权衡。一般我们限定其遍历的深度为6（目前多数的象棋游戏也是这么设定的）。

于是，我们站在MAX的角度，评估函数会是这样子的：

Java代码

static final int INFINITY = 100 ; // 表示无穷的值
static final int WIN = +INFINITY ; // MAX的最大利益为正无穷
static final int LOSE = -INFINITY ; // MAX的最小得益（即MIN的最大得益）为负无穷
static final int DOUBLE_LINK = INFINITY / 2 ; // 如果同一行、列或对角上连续有两个，赛点
static final int INPROGRESS = 1 ; // 仍可继续下（没有胜出或和局）
static final int DRAW = 0 ; // 和局
static final int [][] WIN_STATUS = {
{ 0, 1, 2 },
{ 3, 4, 5 },
{ 6, 7, 8 },
{ 0, 3, 6 },
{ 1, 4, 7 },
{ 2, 5, 8 },
{ 0, 4, 8 },
{ 2, 4, 6 }
};
/**
* 估值函数，提供一个启发式的值，决定了游戏AI的高低
*/
public int gameState( char [] board ) {
int result = INPROGRESS;
boolean isFull = true ;
// is game over?
for ( int pos = 0; pos < 9; pos++) {
char chess = board[pos];
if ( empty == chess) {
isFull = false ;
break ;
}
}
// is Max win/lose?
for ( int [] status : WIN_STATUS) {
char chess = board[status[0]];
if (chess == empty ) {
break ;
}
int i = 1;
for (; i < status.length; i++) {
if (board[status[i]] != chess) {
break ;
}
}
if (i == status.length) {
result = chess == x ? WIN : LOSE;
break ;
}
}
if (result != WIN & result != LOSE) {
if (isFull) {
// is draw
result = DRAW;
} else {
// check double link
// finds[0]->'x', finds[1]->'o'
int [] finds = new int [2];
for ( int [] status : WIN_STATUS) {
char chess = empty ;
boolean hasEmpty = false ;
int count = 0;
for ( int i = 0; i < status.length; i++) {
if (board[status[i]] == empty ) {
hasEmpty = true ;
} else {
if (chess == empty ) {
chess = board[status[i]];
}
if (board[status[i]] == chess) {
count++;
}
}
}
if (hasEmpty && count > 1) {
if (chess == x ) {
finds[0]++;
} else {
finds[1]++;
}
}
}
// check if two in one line
if (finds[1] > 0) {
result = -DOUBLE_LINK;
} else if (finds[0] > 0) {
result = DOUBLE_LINK;
}
}
}
return result;
}

static   final   int   INFINITY = 100 ;   // 表示无穷的值
static   final   int   WIN = +INFINITY ;   // MAX的最大利益为正无穷
static   final   int   LOSE = -INFINITY ;   // MAX的最小得益（即MIN的最大得益）为负无穷
static   final   int   DOUBLE_LINK = INFINITY / 2 ;   // 如果同一行、列或对角上连续有两个，赛点
static   final   int   INPROGRESS = 1 ;   // 仍可继续下（没有胜出或和局）
static   final   int   DRAW = 0 ;   // 和局
static   final   int [][] WIN_STATUS =   {
      {   0, 1, 2 },
      { 3, 4, 5 },
      { 6, 7, 8 },
      { 0, 3, 6 },
      { 1, 4, 7 },
      { 2, 5, 8 },
      { 0, 4, 8 },
      { 2, 4, 6   }
};
/**
 * 估值函数，提供一个启发式的值，决定了游戏AI的高低
 */
public   int   gameState( char []   board )   {
       int   result = INPROGRESS;
       boolean   isFull =   true ;
      
       // is game over?
       for   ( int   pos = 0; pos < 9; pos++) {
             char   chess = board[pos];
             if   ( empty   == chess) {
                  isFull =   false ;
                   break ;
            }
      }
       // is Max win/lose?
       for   ( int [] status : WIN_STATUS) {
             char   chess = board[status[0]];
             if   (chess ==   empty ) {
                   break ;
            }
             int   i = 1;
             for   (; i < status.length; i++) {
                   if   (board[status[i]] != chess) {
                         break ;
                  }
            }
             if   (i == status.length) {
                  result = chess ==   x   ? WIN : LOSE;
                   break ;
            }
      }
       if   (result != WIN & result != LOSE) {
             if   (isFull) {
                   // is draw
                  result = DRAW;
            }   else   {
                   // check double link
                   // finds[0]->'x', finds[1]->'o'
                   int [] finds =   new   int [2];
                   for   ( int [] status : WIN_STATUS) {
                         char   chess =   empty ;
                         boolean   hasEmpty =   false ;
                         int   count = 0;
                         for   ( int   i = 0; i < status.length; i++) {
                               if   (board[status[i]] ==   empty ) {
                                    hasEmpty =   true ;
                              }   else   {
                                     if   (chess ==   empty ) {
                                          chess = board[status[i]];
                                    }
                                     if   (board[status[i]] == chess) {
                                          count++;
                                    }
                              }
                        }
                         if   (hasEmpty && count > 1) {
                               if   (chess ==   x ) {
                                    finds[0]++;
                              }   else   {
                                    finds[1]++;
                              }
                        }
                  }
                   // check if two in one line
                   if   (finds[1] > 0) {
                        result = -DOUBLE_LINK;
                  }   else   if   (finds[0] > 0) {
                        result = DOUBLE_LINK;
                  }
            }
      }
       return   result;
}

基于这些，一个限定层数的实现是这样的：

Java代码

/**
* 以'x'的角度来考虑的极小极大算法
*/
public int minimax( char [] board, int depth){
int [] bestMoves = new int [9];
int index = 0;
int bestValue = - INFINITY ;
for ( int pos=0; pos<9; pos++){
if (board[pos]== empty ){
board[pos] = x ;
int value = min(board, depth);
if (value>bestValue){
bestValue = value;
index = 0;
bestMoves[index] = pos;
} else
if (value==bestValue){
index++;
bestMoves[index] = pos;
}
board[pos] = empty ;
}
}
if (index>1){
index = ( new Random (System. currentTimeMillis ()).nextInt()>>>1)%index;
}
return bestMoves[index];
}
/**
* 对于'x'，估值越大对其越有利
*/
public int max( char [] board, int depth){
int evalValue = gameState (board);
boolean isGameOver = (evalValue== WIN || evalValue== LOSE || evalValue== DRAW );
if (depth==0 || isGameOver){
return evalValue;
}
int bestValue = - INFINITY ;
for ( int pos=0; pos<9; pos++){
if (board[pos]== empty ){
// try
board[pos] = x ;
// maximixing
bestValue = Math. max (bestValue, min(board, depth-1));
// reset
board[pos] = empty ;
}
}
return evalValue;
}
/**
* 对于'o'，估值越小对其越有利
*/
public int min( char [] board, int depth){
int evalValue = gameState (board);
boolean isGameOver = (evalValue== WIN || evalValue== LOSE || evalValue== DRAW );
if (depth==0 || isGameOver){
return evalValue;
}
int bestValue = + INFINITY ;
for ( int pos=0; pos<9; pos++){
if (board[pos]== empty ){
// try
board[pos] = o ;
// minimixing
bestValue = Math.min(bestValue, max(board, depth-1));
// reset
board[pos] = empty ;
}
}
return evalValue;
}

/**
 * 以'x'的角度来考虑的极小极大算法
 */
public   int   minimax( char [] board,   int   depth){
       int [] bestMoves =   new   int [9];
       int   index = 0;
      
       int   bestValue = - INFINITY ;
       for ( int   pos=0; pos<9; pos++){
            
             if (board[pos]== empty ){
                  board[pos] =   x ;
                  
                   int   value = min(board, depth);
                   if (value>bestValue){
                        bestValue = value;
                        index = 0;
                        bestMoves[index] = pos;
                  } else
                   if (value==bestValue){
                        index++;
                        bestMoves[index] = pos;
                  }
                  
                  board[pos] =   empty ;
            }
            
      }
      
       if (index>1){
            index = ( new   Random (System. currentTimeMillis ()).nextInt()>>>1)%index;
      }
       return   bestMoves[index];
      
}
/**
 * 对于'x'，估值越大对其越有利
 */
public   int   max( char [] board,   int   depth){
      
       int   evalValue =   gameState (board);
      
       boolean   isGameOver = (evalValue== WIN   || evalValue== LOSE   || evalValue== DRAW );
       if (depth==0 || isGameOver){
             return   evalValue;
      }
      
       int   bestValue = - INFINITY ;
       for ( int   pos=0; pos<9; pos++){
            
             if (board[pos]== empty ){
                   // try
                  board[pos] =   x ;
                  
                   //   maximixing
                  bestValue = Math. max (bestValue, min(board, depth-1));
                  
                   // reset
                  board[pos] =   empty ;
            }
            
      }
      
       return   evalValue;
      
}
/**
 * 对于'o'，估值越小对其越有利
 */
public   int   min( char [] board,   int   depth){
      
       int   evalValue =   gameState (board);
      
       boolean   isGameOver = (evalValue== WIN   || evalValue== LOSE   || evalValue== DRAW );
       if (depth==0 || isGameOver){
             return   evalValue;
      }
      
       int   bestValue = + INFINITY ;
       for ( int   pos=0; pos<9; pos++){
            
             if (board[pos]== empty ){
                   // try
                  board[pos] =   o ;
                  
                   //   minimixing
                  bestValue = Math.min(bestValue, max(board, depth-1));
                  
                   // reset
                  board[pos] =   empty ;
            }
            
      }
      
       return   evalValue;
      
}

Alpha-beta剪枝

另外，通过结合Alpha-beta剪枝能进一步优化效率。Alpha-beta剪枝顾名思义就是裁剪掉一些不必要的分支，以减少遍历的节点数。实际上是通过传递两个参数alpha和beta到递归的极小极大函数中，alpha表示了MAX的最坏情况，beta表示了MIN的最坏情况，因此他们的初始值为负无穷和正无穷。在递归的过程中，在轮到MAX的回合，如果极小极大的值比alpha大，则更新alpha；在MIN的回合中，如果极小极大值比beta小，则更新beta。当alpha和beta相交时（即alpha>=beta），这时该节点的所有子节点对于MAX和MIN双方都不会带来好的获益，所以可以忽略掉（裁剪掉）以该节点为父节点的整棵子树。

根据这一定义，可以很轻易地在上面程序的基础上进行改进：

Java代码

/**
* 以'x'的角度来考虑的极小极大算法
*/
public int minimax( char [] board, int depth){
int [] bestMoves = new int [9];
int index = 0;
int bestValue = - INFINITY ;
for ( int pos=0; pos<9; pos++){
if (board[pos]== empty ){
board[pos] = x ;
int value = min(board, depth, - INFINITY , + INFINITY );
if (value>bestValue){
bestValue = value;
index = 0;
bestMoves[index] = pos;
} else
if (value==bestValue){
index++;
bestMoves[index] = pos;
}
board[pos] = empty ;
}
}
if (index>1){
index = ( new Random (System. currentTimeMillis ()).nextInt()>>>1)%index;
}
return bestMoves[index];
}
/**
* 对于'x'，估值越大对其越有利
*/
public int max( char [] board, int depth, int alpha, int beta){
int evalValue = gameState (board);
boolean isGameOver = (evalValue== WIN || evalValue== LOSE || evalValue== DRAW );
if (beta<=alpha){
return evalValue;
}
if (depth==0 || isGameOver){
return evalValue;
}
int bestValue = - INFINITY ;
for ( int pos=0; pos<9; pos++){
if (board[pos]== empty ){
// try
board[pos] = x ;
// maximixing
bestValue = Math. max (bestValue, min(board, depth-1, Math. max (bestValue, alpha), beta));
// reset
board[pos] = empty ;
}
}
return evalValue;
}
/**
* 对于'o'，估值越小对其越有利
*/
public int min( char [] board, int depth, int alpha, int beta){
int evalValue = gameState (board);
boolean isGameOver = (evalValue== WIN || evalValue== LOSE || evalValue== DRAW );
if (alpha>=beta){
return evalValue;
}
// try
if (depth==0 || isGameOver || alpha>=beta){
return evalValue;
}
int bestValue = + INFINITY ;
for ( int pos=0; pos<9; pos++){
if (board[pos]== empty ){
// try
board[pos] = o ;
// minimixing
bestValue = Math.min(bestValue, max(board, depth-1, alpha, Math.min(bestValue, beta)));
// reset
board[pos] = empty ;
}
}
return evalValue;
}

/**
 * 以'x'的角度来考虑的极小极大算法
 */
public   int   minimax( char [] board,   int   depth){
       int [] bestMoves =   new   int [9];
       int   index = 0;
      
       int   bestValue = - INFINITY ;
       for ( int   pos=0; pos<9; pos++){
            
             if (board[pos]== empty ){
                  board[pos] =   x ;
                  
                   int   value = min(board, depth, - INFINITY , + INFINITY );
                   if (value>bestValue){
                        bestValue = value;
                        index = 0;
                        bestMoves[index] = pos;
                  } else
                   if (value==bestValue){
                        index++;
                        bestMoves[index] = pos;
                  }
                  
                  board[pos] =   empty ;
            }
            
      }
      
       if (index>1){
            index = ( new   Random (System. currentTimeMillis ()).nextInt()>>>1)%index;
      }
       return   bestMoves[index];
      
}
/**
 * 对于'x'，估值越大对其越有利
 */
public   int   max( char [] board,   int   depth,   int   alpha,   int   beta){
      
       int   evalValue =   gameState (board);
      
       boolean   isGameOver = (evalValue== WIN   || evalValue== LOSE   || evalValue== DRAW );
       if (beta<=alpha){
             return   evalValue;
      }
       if (depth==0 || isGameOver){
             return   evalValue;
      }
      
       int   bestValue = - INFINITY ;
       for ( int   pos=0; pos<9; pos++){
            
             if (board[pos]== empty ){
                   // try
                  board[pos] =   x ;
                  
                   //   maximixing
                  bestValue = Math. max (bestValue, min(board, depth-1, Math. max (bestValue, alpha), beta));
                  
                   // reset
                  board[pos] =   empty ;
            }
            
      }
      
       return   evalValue;
      
}
/**
 * 对于'o'，估值越小对其越有利
 */
public   int   min( char [] board,   int   depth,   int   alpha,   int   beta){
      
       int   evalValue =   gameState (board);
      
       boolean   isGameOver = (evalValue== WIN   || evalValue== LOSE   || evalValue== DRAW );
       if (alpha>=beta){
             return   evalValue;
      }
       // try
       if (depth==0 || isGameOver || alpha>=beta){
             return   evalValue;
      }
      
       int   bestValue = + INFINITY ;
       for ( int   pos=0; pos<9; pos++){
            
             if (board[pos]== empty ){
                   // try
                  board[pos] =   o ;
                  
                   //   minimixing
                  bestValue = Math.min(bestValue, max(board, depth-1, alpha, Math.min(bestValue, beta)));
                  
                   // reset
                  board[pos] =   empty ;
            }
            
      }
      
       return   evalValue;
      
}

*这里对极小极大算法的实现只是其中一种可行性，实际上可能会看到很多种不同的实现方式，但道理是一样的。

使用开局库

同时，你会发现，这样做视乎还不够，特别在一开局。我们都知道，中心的位置是最好的，但是按照我们上面的算法，第一步确实随机的...这在深度受限制的情况下就更显得重要了。于是就引申出了开局库的概念，这是我在某个讲象棋AI的网上看到的，就是给初始的棋盘设定一些格局。

针对上面的例子，我们只要判断是否第一步棋，如果是则想办法让他选择中心的位置（4）。

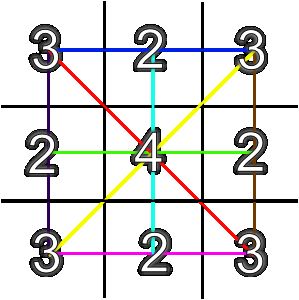
在WIKI百科中找到一幅图也能作为TIC-TAC-TOE开局库的参考：

于是，估算函数会变成这样的（当然也可以在别的地方修改，只要合理）：

Java代码

//开局时，每个位置的估值
static final int [] INITIAL_POS_VALUE = {
3, 2, 3,
2, 4, 2,
3, 2, 3
};
/**
* 估值函数，提供一个启发式的值，决定了游戏AI的高低
*/
public int gameState ( char [] board ) {
int result = INPROGRESS ;
boolean isFull = true ;
int sum = 0;
int index = 0;
// is game over?
for ( int pos=0; pos<9; pos++){
char chess = board[pos];
if ( empty ==chess){
isFull = false ;
} else {
sum += chess;
index = pos;
}
}
// 如果是初始状态，则使用开局库
boolean isInitial = (sum== x ||sum== o );
if (isInitial){
return (sum== x ?1:-1)*INITIAL_POS_VALUE[index];
}
// is Max win/lose?
for ( int [] status : WIN_STATUS ){
char chess = board[status[0]];
if (chess== empty ){
break ;
}
int i = 1;
for (; i
if (board[status[i]]!=chess){
break ;
}
}
if (i==status.length){
result = chess== x ? WIN : LOSE ;
break ;
}
}
if (result!= WIN & result!= LOSE ){
if (isFull){
// is draw
result = DRAW ;
} else {
// check double link
// finds[0]->'x', finds[1]->'o'
int [] finds = new int [2];
for ( int [] status : WIN_STATUS ){
char chess = empty ;
boolean hasEmpty = false ;
int count = 0;
for ( int i=0; i
if (board[status[i]]== empty ){
hasEmpty = true ;
} else {
if (chess== empty ){
chess = board[status[i]];
}
if (board[status[i]]==chess){
count++;
}
}
}
if (hasEmpty && count>1){
if (chess== x ){
finds[0]++;
} else {
finds[1]++;
}
}
}
// check if two in one line
if (finds[1]>0){
result = - DOUBLE_LINK ;
} else
if (finds[0]>0){
result = DOUBLE_LINK ;
}
}
}
return result;
}

转载地址：http://univasity.iteye.com/blog/1170216

CTF 竞赛密码学方向学习路径规划 David Max CTF 学习笔记密码学 ctf 信息安全
目录计算机科学基础计算机科学概念的引入、兴趣的引导开发环境的配置与常用工具的安装WattToolkit（Steam++）、机场代理Scoop（Windows用户可选）常用Python库SageMathLinux小工具yafuOpenSSLMarkdown编程基础Python其他编程语言、算法与数据结构（可选）数学基础离散数学与抽象代数复杂性分析密码学的正式学习兴趣的培养做题小技巧系统学习需要了解并
C++算法与数据结构闻缺陷则喜何志丹 #算法基础算法数据结构 c++动态规划图论背包问题贪心
求职的感想学历、证书、名气都是敲门砖，大大提高面试机会。能否入职主要取决于：a，项目（行业）经验。b，编程语言的熟练程度。c，算法水平。对于某个具体公司，a>b>c，对于所有公司ab>c，长期而言a
350页前端校招面试题直击大厂：前端基础、前端核心、计算机基础、项目、Hr面 2401_86400095 前端
**1.HTML2.CSS3.前端基础4.前端核心5.前端进阶6.移动端开发7.计算机基础8.算法与数据结构9.设计模式10.项目11.职业发展12.Hr面**正文HTML1.浏览器页面有哪三层构成，分别是什么，作用是什么?2.HTML5的优点与缺点？3.Doctype作用?严格模式与混杂模式如何区分？它们有何意义?4.HTML5有哪些新特性、移除了哪些元素？5.你做的网页在哪些浏览器测试过,这些
计算机专业考研书目（中科大） FQLSY
考研408计算机学科专业基础综合一、数据结构1.教材：《数据结构》严蔚敏清华大学出版社清华大学严蔚敏的这本数据结构的教材是国内数据结构教材的权威。也是国内使用最广，其广度远远超越其他同类教材，计算机考研专业课命题必定以它为蓝本。这一本数据结构是2007年的最新版本，完全适合任何学校的考研数据结构的复习之用，是数据结构学习最权威的教材。2.辅导书：《算法与数据结构考研试题精析（第二版）》机械工业出版
Java实现家谱家族管理系统，图形化家谱家族树，单机应用程序 violet_ever_garden java javafx 家谱树 JAVA 图形用户界面设计源代码
背景算法与数据结构实验内容，使用Java+JavaFX，花了两个星期独自完成。功能（1）普通用户、超级管理员不同角色，不同角色登录后的权限各不相同，普通用户可以进行查询；超级管理员有对所有成员增加、删除和修改的权限。现在的初始超级管理员：admin123456初始普通用户：user555123123（2）家谱中成员的信息中包含姓名、出生日期、婚否、地址、健在否、死亡日期（若其已死亡）等（3）数据以
面试算法LeetCode刷题班—BAT面试官带你刷真题、过笔试 Dan Boneh 高级程序设计算法
课程名称:《面试算法LeetCode刷题班》——BAT面试官带你刷真题、过笔试主讲老师:林老师BAT资深研发工程师(T7/P8级)，致力于搜索引擎及其子系统的研发、迭代与优化，数据分析与挖掘领域专家，多年担任校园招聘、社会招聘面试官，丰富的面试候选人经验。课程简介:掌握算法与数据结构是成为优秀程序员的必经之路，众多国内外知名互联网企业都将算法面试作为程序员招聘的重要和必需途径，只有高效应对各类题目
【算法与数据结构】算法与数据结构知识点晚安66 算法算法
文章目录一、算法和数据结构和LeetCode介绍二、算法和数据结构入门2.1时间复杂度2.2空间复杂度2.3基础排序算法2.3.1选择排序算法2.3.2冒泡排序算法三、数组3.1二分法查找法3.2双指针法四、链表理论五、哈希表理论五、栈和队列理论5.1单调栈六、二叉树理论6.1树的定义6.2二叉树的存储方式6.3二叉树的遍历方式6.4高度和深度七、回溯算法八、贪心算法九、动态规划9.1背包问题9.
【算法与数据结构】42、LeetCode接雨水晚安66 算法算法
文章目录一、题目二、解法三、完整代码所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。一、题目二、解法思路分析：程序如下：复杂度分析：时间复杂度：O()O()O()。空间复杂度：O()O()O()。三、完整代码end
【算法与数据结构】496、503、LeetCode下一个更大元素I II 晚安66 算法算法
文章目录一、496、下一个更大元素I二、503、下一个更大元素II三、完整代码所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。一、496、下一个更大元素I 思路分析：本题思路和【算法与数据结构】739、LeetCode每日温度类似。如果用暴力破解法时间复杂度需要O(m∗n)O(m*n)O(m∗n)，其中mmm和nnn分别是两个数组的长度。单调栈只需要O(
【算法】【数据结构】算法与数据结构的关系琛：D 算法数据结构算法数据结构
程序=算法+数据结构+语言工具和环境但在算法学习过程中，我认识到算法和数据结构是密不可分的，脱离数据结构谈论算法是空架子。算法：解决问题的步骤和方法。对数据进行操作和处理的方法。数据结构：用来存储数据的方式。数据结构和算法之间的关系可以看作是一种相互依赖的关系。在解决问题时，首先需要选择适当的数据结构来存储和组织数据，然后再设计合适的算法对这些数据进行操作和处理。数据结构的选择可以影响算法的效率和
Leetcode64. 最小路径和（C语言） jeanlu 数据结构&算法算法动态规划 c语言
Leetcode64.最小路径和（C语言）算法-动态规划（矩阵路径）：算法与数据结构参考题目：给定一个包含非负整数的mxn网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。每次只能向下或者向右一步，例：输入:[[1,3,1],[1,5,1],[4,2,1]]输出:7思路：动态规划。每个位置存储起点到当前位置的路径和最小值。注意行列下标代码：#definemin(a,b)(a
算法与数据结构--简析红黑树云逸Dean
1.为什么要使用红黑树：可以保证在O（logN）的时间复杂度下做查找删除添加2.性质：（来自于维基百科Red–blacktree条目）节点是红色或者黑色的（Eachnodeiseitherredorblack）根是黑色的,有时会被省略，由于根是黑色和红色对规范并没有其他影响(Therootisblack.Thisruleissometimesomitted.Sincetherootcanalway
【算法与数据结构】583、72、LeetCode两个字符串的删除操作+编辑距离晚安66 算法算法
文章目录一、583、两个字符串的删除操作二、72、编辑距离三、完整代码所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。一、583、两个字符串的删除操作思路分析：本题的思路和115、不同的子序列差不多，只是变成了两个字符串都能删除字符。第一步，动态数组的含义。dp[i][j]dp[i][j]dp[i][j]代表使得word1[0,i−1]word1[0,
【算法与数据结构】647、516、LeetCode回文子串+最长回文子序列晚安66 算法算法
文章目录一、647、回文子串二、516、最长回文子序列三、完整代码所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。一、647、回文子串思路分析：判断一个字符串是否为回文串那么必须确定回文串的所在区间，而一维数组无法描述区间，因此我们需要用一个二维的dp数组来表示。我们只需要统计dp数组中回文串的个数即可。第一步，动态数组的含义。dp[i][j]dp[i
【算法与数据结构】718、1143、1035、392、115、LeetCode最长重复子数组+最长公共子序列+不相交的线+判断子序列+不同的子序列晚安66 算法算法
文章目录一、718、最长重复子数组二、1143、最长公共子序列三、1035、不相交的线四、392、判断子序列五、115、不同的子序列六、完整代码所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。一、718、最长重复子数组思路分析：第一步，动态数组的含义。dp[i][j]dp[i][j]dp[i][j]代表以下标i−1i-1i−1为结尾的nums1，和以下
【算法与数据结构】739、LeetCode每日温度晚安66 算法算法
文章目录一、题目二、解法三、完整代码所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。一、题目二、解法思路分析：程序如下：复杂度分析：时间复杂度：O()O()O()。空间复杂度：O()O()O()。三、完整代码end
python算法与数据结构（搜索算法和拓扑排序算法）---广度优先搜索和拓扑排序他是只猫算法 python 数据结构 BFS 广度优先
广度优先搜索BFS定义&基本内容广度优先是按照层次由近及远的进行搜索，在当前层次所有可及节点都搜索完毕后才会继续往下搜索，其本质就是寻找从起点到终点的最短路程。树的广度优先搜索树的广度优先遍历，可以看成是层序遍历。访问顺序如图：图的广度优先搜索有向图：边存在方向的图；有向图中度分为入度（in-degree）和出度（out-degree）入度：表示有多少条边指向这个顶点；出度：表示有多少条边是以这个
python算法与数据结构---动态规划他是只猫算法 python 数据结构动态规划
动态规划记不住过去的人，注定要重蹈覆辙。定义对于一个模型为n的问题，将其分解为k个规模较小的子问题（阶段），按顺序求解子问题，前一子问题的解，为后一子问题提供有用的信息。在求解任一子问题时，通过决策求得局部最优解，依次解决各子问题。最后通过简单的判断，得到原问题的解。经典案例—斐波那契数列斐波那契数列又称黄金分割数列。因数学家莱昂纳多-斐波那契以兔子繁殖为例引入，故又称兔子数列。1,1,2,3,5
【考研408】算法与数据结构笔记 newcih 408 算法与数据结构考研
文章目录绪论数据结构的基本概念算法和算法评价线性表线性表的定义和基本操作线性表的顺序表示线性表的链式表示栈和队列栈基本操作栈的顺序存储结构栈的链式存储队列队列常见的基本操作队列的顺序存储结构队列的链式存储结构双端队列栈和队列的应用栈在括号匹配中的应用栈在表达式求值中的应用栈在递归中的应用队列在层次遍历中的应用队列在计算机系统中的应用特殊矩阵的压缩存储数组的定义数组的存储结构矩阵的压缩存储串串的定义
第十五章 Caché 算法与数据结构堆排序 Cache技术分享
第十五章Caché算法与数据结构堆排序二叉堆特性最大堆的堆顶是整个堆中的最大元素。最小堆的堆顶是整个堆中的最小元素。调整以最大堆为例，如果删除一个最大堆的堆顶（并不是完全删除，而是跟末尾的节点交换位置），经过自我调整，第2大的元素就会被交换上来，成为最大堆的新堆顶。image.png如上图所示，在删除值为10的堆顶节点后，经过调整，值为9的新节点就会顶替上来；在删除值为9的堆顶节点后，经过调整，值
有事没事，研究研究算法乌龟的慢生活
图片发自App图片发自App有点意思，算法很有意思的。学习经典算法与数据结构。看图说话，然后代码实现！然后解答实际问题。有意思的。利用好这些软件。
南京邮电大学算法与数据结构设计：文本的加密与解密、校园导航系统一直是我呀课程设计开源算法数据结构 qt c++课程设计
作者：由于文件数量过多，逐个上传较为繁琐，所以文章中上传的代码只是部分主要的结构，需要源码的小伙伴可以去我的Github上搜索，地址为：GitHub-xxz1314520/Algorithm-and-Program-Design-of-NJUPT:这是我在南京邮电大学计算机学院所开设的课程《算法与数据结构设计》写的项目A.文本的加密和解密一、课题内容和要求设计要求：设计对已知文本进行加密和解密程序
【算法与数据结构】121、122、123、188、309、714、LeetCode买卖股票的最佳时机I II III IV+含冷冻期+含手续费晚安66 算法算法
文章目录一、121、LeetCode买卖股票的最佳时机1.1动态规划1.2动态规划-滚动数组二、122、买卖股票的最佳时机II三、123、买卖股票的最佳时机III四、188、买卖股票的最佳时机IV五、309、买卖股票的最佳时机含冷冻期六、714、买卖股票的最佳时机含手续费七、完整代码所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。一、121、LeetCod
【算法与数据结构】300、LeetCode最长递增子序列晚安66 算法算法
文章目录一、题目二、解法三、完整代码所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。一、题目二、解法思路分析：程序如下：classSolution{public:intlengthOfLIS(vector&nums){vectordp(nums.size(),1);intresult=1;for(inti=1;inums[j])dp[i]=max(
算法考试复习 FakeCSer爱去网吧
引论算法与数据结构与程序的区别算法是求解问题的过程描述：从蛮力到策略数据结构是数据的组织与存储：从杂乱无章到井然有序程序=算法+数据结构算法描述自然语言伪代码流程图三种不同的计算机问题判断问题（yes,no）例如输入的数是否大于60优化问题（求最优解）例如从A到B的最短路径是什么数值计算常见的计算机问题排序查找串处理图问题组合问题几何问题数值问题概念什么是算法：算法是一系列解决问题的清晰指令，也就
【Leetcode】算法与数据结构 C语言造夢先森算法与数据结构 C语言进阶 string 函数 leetcode math stack
字符串：https://leetcode-cn.com/problems/reverse-string/voidswap(char*a,char*b){chart=*a;*a=*b,*b=t;}voidreverseString(char*s,intsSize){for(intleft=0,right=sSize-1;left=m||y=n||grid[x][y]=='0')//遇到边界或‘0’直
【算法与数据结构】198、213、337LeetCode打家劫舍I, II, III 晚安66 算法算法
文章目录一、198、打家劫舍二、213、打家劫舍II三、337、打家劫舍III三、完整代码所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。一、198、打家劫舍思路分析：打家劫舍是动态规划的的经典题目。本题的难点在于递归公式和初始化。第一步，dp[j]dp[j]dp[j]的含义。dp[j]dp[j]dp[j]代表到第jjj家的时候，偷窃到的最高金额。第二
「干货」编程语言十大经典算法，你知道几个？蓝桥云课算法数据结构推荐算法
算法与数据结构是计算机学习路上的内功心法，也是学好编程语言的重要基础。今天给大家介绍一下十大经典算法。十大经典算法分别是：冒泡排序，插入排序，选择排序，希尔排序，快速排序，归并排序，桶排序，堆排序，计数排序，基数排序。预备知识：算法稳定性如果a==b，排序前a在b的前面，排序后a在b的后面，只要会出现这种现象，我们则说这个算法不稳定（即使两个相等的数，在排序的过程中不断交换，有可能将后面的b交换到
【算法与数据结构】139、LeetCode单词拆分晚安66 算法算法
文章目录一、题目二、解法三、完整代码所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。一、题目二、解法思路分析：本题可以看做一个动态规划问题。其中，字符串s是背包，而字典中的单词就是物品。题目问的是单词能否组成字符串s，就是问物品能不能把背包装满。字典中的单词可以重复使用，因此是一个完全背包问题。第一步，dp[j]dp[j]dp[j]的含义。dp[j]d
python算法与数据结构---排序和归并排序茨球是只猫算法数据结构 python 排序算法
学习目标掌握归并排序的基本原理使用python语言解答归并排序题目归并排序原理及过程将两个有序的数组合并成一个有序数组称为从上往下分解：把当前区间一分为二，直至分解为若干个长度为1的子数组从上往下的合并：两个有序的子区域两两向上合并；体现了分治思想，稳定排序复杂度平均时间复杂度：O(NlogN)最坏时间复杂度：O(NlogN)归并排序合并过程temp数组用于存储合并结果，合并后拷贝回原数组；双指针
github中多个平台共存 jackyrong github
在个人电脑上，如何分别链接比如oschina,github等库呢，一般教程之列的，默认 ssh链接一个托管的而已，下面讲解如何放两个文件 1）设置用户名和邮件地址 $ git config --global user.name "xx" $ git config --global user.email "[email protected]"
ip地址与整数的相互转换(javascript) alxw4616 JavaScript
//IP转成整型 function ip2int(ip){ var num = 0; ip = ip.split("."); num = Number(ip[0]) * 256 * 256 * 256 + Number(ip[1]) * 256 * 256 + Number(ip[2]) * 256 + Number(ip[3]); n
读书笔记-jquey+数据库+css chengxuyuancsdn html jquery oracle
1、grouping ,group by rollup, GROUP BY GROUPING SETS区别 2、$("#totalTable tbody>tr td:nth-child(" + i + ")").css({"width":tdWidth, "margin":"0px", &q
javaSE javaEE javaME == API下载 Array_06 java
oracle下载各种API文档： http://www.oracle.com/technetwork/java/embedded/javame/embed-me/documentation/javame-embedded-apis-2181154.html JavaSE文档： http://docs.oracle.com/javase/8/docs/api/ JavaEE文档： ht
shiro入门学习 cugfy java Web 框架
声明本文只适合初学者，本人也是刚接触而已，经过一段时间的研究小有收获，特来分享下希望和大家互相交流学习。首先配置我们的web.xml代码如下，固定格式，记死就成 <filter> <filter-name>shiroFilter</filter-name> &nbs
Array添加删除方法 357029540 js
刚才做项目前台删除数组的固定下标值时，删除得不是很完整，所以在网上查了下，发现一个不错的方法，也提供给需要的同学。 //给数组添加删除 Array.prototype.del = function(n){
navigation bar 更改颜色张亚雄 IO
今天郁闷了一下午，就因为objective-c默认语言是英文，我写的中文全是一些乱七八糟的样子，到不是乱码，但是，前两个自字是粗体，后两个字正常体，这可郁闷死我了，问了问大牛，人家告诉我说更改一下字体就好啦，比如改成黑体，哇塞，茅塞顿开。翻书看，发现，书上有介绍怎么更改表格中文字字体的，代码如下
unicode转换成中文 adminjun unicode 编码转换
在Java程序中总会出现\u6b22\u8fce\u63d0\u4ea4\u5fae\u535a\u641c\u7d22\u4f7f\u7528\u53cd\u9988\uff0c\u8bf7\u76f4\u63a5这个的字符，这是unicode编码，使用时有时候不会自动转换成中文就需要自己转换了使用下面的方法转换一下即可。 /** * unicode 转换成中文
一站式 Java Web 框架 firefly aijuans Java Web
Firefly是一个高性能一站式Web框架。涵盖了web开发的主要技术栈。包含Template engine、IOC、MVC framework、HTTP Server、Common tools、Log、Json parser等模块。 firefly-2.0_07修复了模版压缩对javascript单行注释的影响，并新增了自定义错误页面功能。更新日志：增加自定义系统错误页面功能
设计模式——单例模式 ayaoxinchao 设计模式
定义 Java中单例模式定义：“一个类有且仅有一个实例，并且自行实例化向整个系统提供。” 分析从定义中可以看出单例的要点有三个：一是某个类只能有一个实例；二是必须自行创建这个实例；三是必须自行向系统提供这个实例。 &nb
Javascript 多浏览器兼容性问题及解决方案 BigBird2012 JavaScript
不论是网站应用还是学习js,大家很注重ie与firefox等浏览器的兼容性问题，毕竟这两中浏览器是占了绝大多数。一、document.formName.item(”itemName”) 问题问题说明：IE下，可以使用 document.formName.item(”itemName”) 或 document.formName.elements ["elementName&quo
JUnit-4.11使用报java.lang.NoClassDefFoundError: org/hamcrest/SelfDescribing错误 bijian1013 junit4.11 单元测试
下载了最新的JUnit版本，是4.11，结果尝试使用发现总是报java.lang.NoClassDefFoundError: org/hamcrest/SelfDescribing这样的错误，上网查了一下，一般的解决方案是，换一个低一点的版本就好了。还有人说，是缺少hamcrest的包。去官网看了一下，如下发现：
[Zookeeper学习笔记之二]Zookeeper部署脚本 bit1129 zookeeper
Zookeeper伪分布式安装脚本(此脚本在一台机器上创建Zookeeper三个进程，即创建具有三个节点的Zookeeper集群。这个脚本和zookeeper的tar包放在同一个目录下，脚本中指定的名字是zookeeper的3.4.6版本，需要根据实际情况修改)： #!/bin/bash #!!!Change the name!!! #The zookeepe
【Spark八十】Spark RDD API二 bit1129 spark
coGroup package spark.examples.rddapi import org.apache.spark.{SparkConf, SparkContext} import org.apache.spark.SparkContext._ object CoGroupTest_05 { def main(args: Array[String]) { v
Linux中编译apache服务器modules文件夹缺少模块(.so)的问题 ronin47 modules
在modules目录中只有httpd.exp，那些so文件呢？我尝试在fedora core 3中安装apache 2. 当我解压了apache 2.0.54后使用configure工具并且加入了 --enable-so 或者 --enable-modules=so (两个我都试过了) 去make并且make install了。我希望在/apache2/modules/目录里有各种模块，
Java基础-克隆 BrokenDreams java基础
Java中怎么拷贝一个对象呢？可以通过调用这个对象类型的构造器构造一个新对象，然后将要拷贝对象的属性设置到新对象里面。Java中也有另一种不通过构造器来拷贝对象的方式，这种方式称为克隆。 Java提供了java.lang.
读《研磨设计模式》-代码笔记-适配器模式-Adapter bylijinnan java 设计模式
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ package design.pattern; /* * 适配器模式解决的主要问题是，现有的方法接口与客户要求的方法接口不一致 * 可以这样想，我们要写这样一个类（Adapter）: * 1.这个类要符合客户的要求 ---> 那显然要
HDR图像PS教程集锦&心得 cherishLC PS
HDR是指高动态范围的图像，主要原理为提高图像的局部对比度。软件有photomatix和nik hdr efex。一、教程叶明在知乎上的回答： http://www.zhihu.com/question/27418267/answer/37317792 大意是修完后直方图最好是等值直方图，方法是HDR软件调一遍，再结合不透明度和蒙版细调。二、心得 1、去除阴影部分的
maven-3.3.3 mvn archetype 列表 crabdave ArcheType
maven-3.3.3 mvn archetype 列表可以参考最新的：http://repo1.maven.org/maven2/archetype-catalog.xml [INFO] Scanning for projects... [INFO]
linux shell 中文件编码查看及转换方法 daizj shell 中文乱码 vim 文件编码
一、查看文件编码。在打开文件的时候输入:set fileencoding 即可显示文件编码格式。二、文件编码转换 1、在Vim中直接进行转换文件编码,比如将一个文件转换成utf-8格式 &
MySQL--binlog日志恢复数据 dcj3sjt126com binlog
恢复数据的重要命令如下 mysql> flush logs; 默认的日志是mysql-bin.000001，现在刷新了重新开启一个就多了一个mysql-bin.000002
数据库中数据表数据迁移方法 dcj3sjt126com sql
刚开始想想好像挺麻烦的，后来找到一种方法了，就SQL中的 INSERT 语句，不过内容是现从另外的表中查出来的，其实就是 MySQL中INSERT INTO SELECT的使用下面看看如何使用语法：MySQL中INSERT INTO SELECT的使用 1. 语法介绍有三张表a、b、c，现在需要从表b
Java反转字符串 dyy_gusi java 反转字符串
前几天看见一篇文章，说使用Java能用几种方式反转一个字符串。首先要明白什么叫反转字符串，就是将一个字符串到过来啦，比如"倒过来念的是小狗"反转过来就是”狗小是的念来过倒“。接下来就把自己能想到的所有方式记录下来了。 1、第一个念头就是直接使用String类的反转方法，对不起，这样是不行的，因为Stri
UI设计中我们为什么需要设计动效 gcq511120594 UI linux
随着国际大品牌苹果和谷歌的引领，最近越来越多的国内公司开始关注动效设计了，越来越多的团队已经意识到动效在产品用户体验中的重要性了，更多的UI设计师们也开始投身动效设计领域。但是说到底，我们到底为什么需要动效设计？或者说我们到底需要什么样的动效？做动效设计也有段时间了，于是尝试用一些案例，从产品本身出发来说说我所思考的动效设计。一、加强体验舒适度嗯，就是让用户更加爽更加爽的用
JBOSS服务部署端口冲突问题 HogwartsRow java 应用服务器 jboss server EJB3
服务端口冲突问题的解决方法，一般修改如下三个文件中的部分端口就可以了。 1、jboss5/server/default/conf/bindingservice.beans/META-INF/bindings-jboss-beans.xml 2、./server/default/deploy/jbossweb.sar/server.xml 3、.
第三章 Redis/SSDB+Twemproxy安装与使用 jinnianshilongnian ssdb reids twemproxy
目前对于互联网公司不使用Redis的很少，Redis不仅仅可以作为key-value缓存，而且提供了丰富的数据结果如set、list、map等，可以实现很多复杂的功能；但是Redis本身主要用作内存缓存，不适合做持久化存储，因此目前有如SSDB、ARDB等，还有如京东的JIMDB，它们都支持Redis协议，可以支持Redis客户端直接访问；而这些持久化存储大多数使用了如LevelDB、RocksD
ZooKeeper原理及使用 liyonghui160com
ZooKeeper是Hadoop Ecosystem中非常重要的组件，它的主要功能是为分布式系统提供一致性协调(Coordination)服务，与之对应的Google的类似服务叫Chubby。今天这篇文章分为三个部分来介绍ZooKeeper，第一部分介绍ZooKeeper的基本原理，第二部分介绍ZooKeeper
程序员解决问题的60个策略 pda158 框架工作单元测试
根本的指导方针 1. 首先写代码的时候最好不要有缺陷。最好的修复方法就是让 bug 胎死腹中。良好的单元测试强制数据库约束使用输入验证框架避免未实现的“else”条件在应用到主程序之前知道如何在孤立的情况下使用日志 2. print 语句。往往额外输出个一两行将有助于隔离问题。 3. 切换至详细的日志记录。详细的日
Create the Google Play Account sillycat Google
Create the Google Play Account Having a Google account, pay 25$, then you get your google developer account. References: http://developer.android.com/distribute/googleplay/start.html https://p
JSP三大指令 vikingwei jsp
JSP三大指令一个jsp页面中，可以有0~N个指令的定义！ 1. page --> 最复杂：<%@page language="java" info="xxx"...%> * pageEncoding和contentType： > pageEncoding：它

极大极小值算法

你可能感兴趣的:(算法与数据结构)