【论文解读 AAAI 2020 | HDGI】Heterogeneous Deep Graph Infomax
论文题目:Heterogeneous Deep Graph Infomax
论文来源:AAAI 2020
论文链接:https://arxiv.org/abs/1911.08538v1
代码链接:https://github.com/YuxiangRen/Heterogeneous-Deep-Graph-Infomax
关键词:异质图,表示学习,GNN,互信息,attention
文章目录
- 1 摘要
- 2 引言
- 3 定义
- 4 HDGI方法
- 4.1 HDGI概览
- 4.2 基于元路径的局部表示编码器
- 4.3 全局表示的编码器
- 4.4 HDGI的学习
- 5 实验
- 6 总结
- 参考文献
1 摘要
本文解决的是异质图的表示学习问题。
受基于互信息的学习算法启发,提出了无监督的图神经网络****HDGI(Heterogeneous Deep Graph Infomax),用于异质图的表示学习。
使用元路径建模异质图结构中的语义信息,使用图卷积模块和语义级别的注意力机制捕获节点的局部表示。
通过最大化局部和全局的互信息,HDGI可以有效地学习到高阶的节点表示。
实验显示HDGI超越了state-of-the-art的无监督的图表示学习方法,并且和有监督的用于节点分类的state-of-the-art的GNN模型相比,也表现强劲。
2 引言
有监督的GNN模型不能用于数据标签难获取的任务。
无监督的图表示学习模型
无监督的图表示学习模型大致可分为两类:
(1)基于矩阵分解的模型
通过分解简单的相似度矩阵捕获图的全局信息,但是忽视了节点属性信息以及局部邻居间的关系信息。
(2)基于边的模型
通过节点间的连边或随机游走得到的路径,捕获了局部和高阶邻居的信息。有连边的节点或者是在同一路径中共现的节点,其节点表示更加相似。
基于边的模型倾向于保留有限范围(有限阶)的节点相似度,缺乏保留全局图结构的机制。
(3)DGI(deep graph infomax)
最近的DGI[1]提出了一个新方向,同时考虑了局部和全局的图结构。
DGI最大化了图patch representations间的互信息以及对应的图的high-level summaries。
甚至和同质图的有监督的GNN模型相比,有可与之比拟的效果。
本文贡献
本文作者提出基于互信息的用于异质图表示学习的框架。
(1)第一个在异质图表示学习中应用最大化互信息的工作;
(2)提出HDGI方法,是无监督的GNN模型。在元路径上使用注意力机制来处理异质图的异质性,使用互信息最大化实现无监督的设置。
(3)实验证明HDGI学习得到的节点表示可用于节点分类和节点聚类任务。甚至比有监督信息的state-of-the-art GNN模型表现好。
3 定义
(1)异质图(HG)
- 图 G = ( V , E ) \mathcal{G}=(\mathcal{V}, \mathcal{E}) G=(V,E)
- 节点映射函数: ϕ : V → T \phi: \mathcal{V}\rightarrow \mathcal{T} ϕ:V→T, ϕ ( v ) ∈ T \phi(v)\in \mathcal{T} ϕ(v)∈T
- 边映射函数: ψ : E → R \psi: \mathcal{E}\rightarrow \mathcal{R} ψ:E→R, ψ ( e ) ∈ T \psi(e)\in \mathcal{T} ψ(e)∈T
- ∣ T ∣ + ∣ E ∣ > 2 |\mathcal{T}|+|\mathcal{E}|>2 ∣T∣+∣E∣>2
- 节点的属性特征编码成矩阵 X X X
(2)异质图表示学习
给定 G , X \mathcal{G}, X G,X,学习到低维的节点表示: H ∈ R ∣ V ∣ × d H\in \mathbb{R}^{|\mathcal{V}|\times d} H∈R∣V∣×d。
本文作者只聚焦于学习一种类型的节点的表示,该类型的节点记为 V t \mathcal{V}_t Vt。
元路径表示两节点间的复合关系,元路径集合定义为 { Φ 1 , Φ 2 , . . . , Φ P } {\{\Phi_1, \Phi_2,..., \Phi_P\}} {Φ1,Φ2,...,ΦP}。
本文为了简化问题的设置,使用对称且无向的元路径定义目标节点 V t \mathcal{V}_t Vt间的相似性。
(3)基于元路径的邻接矩阵
给定元路径 Φ i \Phi_i Φi,若节点 v i ∈ V t , v j ∈ V t v_i\in \mathcal{V}_t, v_j\in \mathcal{V}_t vi∈Vt,vj∈Vt间存在一个元路径实例,则 v i , v j v_i, v_j vi,vj就是基于 Φ i \Phi_i Φi的邻居。
这样的邻居信息表示成基于元路径的邻接矩阵: A Φ i ∈ R ∣ V t ∣ × ∣ V t ∣ A^{\Phi_i}\in \mathbb{R}^{|\mathcal{V}_t|\times |\mathcal{V}_t|} AΦi∈R∣Vt∣×∣Vt∣。若 v i , v j v_i, v_j vi,vj通过元路径 Φ i \Phi_i Φi相连,则 A i j Φ i = A j i Φ i = 1 A^{\Phi_i}_{ij}=A^{\Phi_i}_{ji}=1 AijΦi=AjiΦi=1,否则为0。
4 HDGI方法
4.1 HDGI概览
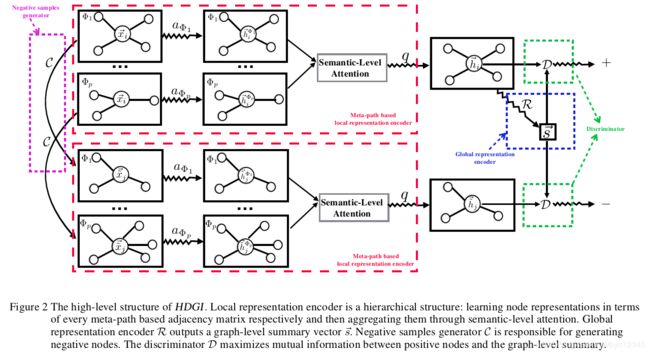
HDGI的概览如图2所示。
输入是: G , X ∈ R N × d , { Φ i } i = 1 P \mathcal{G}, X\in \mathbb{R}^{N\times d}, {\{\Phi_i\}^P_{i=1}} G,X∈RN×d,{Φi}i=1P。
可计算出基于元路径的邻接矩阵集合: { A Φ i } i = 1 P {\{A^{\Phi_i}\}^P_{i=1}} {AΦi}i=1P。
(1)4.2节展示了基于元路径的局部表示编码,由两步组成:
- 根据 X X X和每个 A Φ i A^{\Phi_i} AΦi学习到节点表示 H Φ i H^{\Phi_i} HΦi;
- 使用语义级别的注意力机制聚合 { H Φ i } i = 1 P {\{H^{\Phi_i}\}^P_{i=1}} {HΦi}i=1P,生成节点表示 H H H。
(2)4.3节展示了全局的表示编码器 R \mathcal{R} R,从 H H H获得图的summary vector s ⃗ \vec{s} s。最大化正样本和graph-level summary s ⃗ \vec{s} s间的互信息,以训练判别器 D \mathcal{D} D。
(3)4.4节展示了基于互信息的判别器 D \mathcal{D} D以及负样本生成器 C \mathcal{C} C。
4.2 基于元路径的局部表示编码器
(1)针对特定元路径的图节点表示学习
使用node-level编码器,编码节点特征 X X X和元路径 A Φ i A^{\Phi_i} AΦi:
- GCN
其中 A Φ i ^ = A Φ i + I \hat{A^{\Phi_i}}=A^{\Phi_i}+I AΦi^=AΦi+I, D Φ i D^{\Phi_i} DΦi是 A Φ i ^ \hat{A^{\Phi_i}} AΦi^的节点度对角矩阵。矩阵 W Φ i ∈ R d × F W^{\Phi_i}\in \mathbb{R}^{d\times F} WΦi∈Rd×F是滤波器参数。
- GAT
对于第 m m m个节点,其K-head attention输出可计算为:

N m Φ i \mathcal{N}^{\Phi_i}_m NmΦi是节点 m m m基于 Φ i \Phi_i Φi的邻居节点集合, α m j Φ i , k \alpha^{\Phi_i, k}_{mj} αmjΦi,k是第 k k k个归一化后的注意力系数。
节点级别的学习之后,得到了一组节点表示 { H Φ i } m = 1 P {\{H^{\Phi_i}\}^P_{m=1}} {HΦi}m=1P,接着将其聚合得到基于异质图的节点表示。
(2)异质图节点表示学习(聚合不同元路径)
受HAN的启发,使用语义注意力层 L a t t L_{att} Latt,为不同的元路径学习到不同的权重:
不同元路径的重要性计算如下:
使用注意力系数加权聚合:
注意:
HDGI和HAN在学习方式上是有区别的。HAN将分类交叉熵作为损失函数,受训练集中已标注的数据影响。然而,HDGI学习到的注意力权重由二元交叉熵损失指导,表示某一节点是否在原图中。
下一小节介绍全局表示的编码器,它将 H H H作为输入,输出grapg-level summary。
4.3 全局表示的编码器
HDGI的学习目标是最大化局部表示和全局表示间的互信息。
H H H中包含了节点的局部表示,需要计算出表示整个异质图全局信息的summary vector s ⃗ \vec{s} s。
考虑了三个编码函数:
(1)Averaging encoder function
对节点表示取均值作为graph-level summary s ⃗ \vec{s} s:
(2)Pooling encoder function
将每个节点向量单独输入到一个全连接层。使用元素级的max-pooling操作(对应维度的所有元素取最大值),汇总出节点集的信息:
使用基于LSTM的Set2vec,因为原始的set2vec[2]是用于有序的节点序列的。而这里是总结来自每个节点的信息,而不仅仅是图的结构,从而得到图的summary。
将节点的邻居随机排列(无序)作为LSTM的输入。
4.4 HDGI的学习
(1)基于互信息的判别器
Belghazi等人在论文[3]中证明了KL散度符合Donsker-Varadhan representation,并且f-divergence representation是其对偶表示。
这个对偶表示为计算 X , Y X,Y X,Y的副信息提供了下界:
其中, P X Y \mathbb{P}_{XY} PXY是联合分布, P X ⊗ P Y \mathbb{P}_X \otimes \mathbb{P}_Y PX⊗PY是边缘分布的乘积。 T w T_w Tw是基于参数为 w w w的判别器的深度神经网络。
使用 P X Y \mathbb{P}_{XY} PXY和 P X ⊗ P Y \mathbb{P}_X \otimes \mathbb{P}_Y PX⊗PY中的样本可以估计出(10)式中的等号。
这里,通过训练判别器 D \mathcal{D} D,同时估计和最大化互信息,从而辨别出正样本集 P o s = { [ h ⃗ n , s ⃗ ] } n = 1 N Pos={\{[\vec{h}_n, \vec{s}]}\}^N_{n=1} Pos={[hn,s]}n=1N和负样本集 N e g = { [ h ⃗ m , s ⃗ ] } m = 1 M Neg={\{[\vec{h}_m, \vec{s}]}\}^M_{m=1} Neg={[hm,s]}m=1M。
当 h ⃗ i \vec{h}_i hi属于原图(联合分布)时, ( h ⃗ i , s ⃗ ) (\vec{h}_i, \vec{s}) (hi,s)是正样本; h ^ ⃗ j \vec{\hat{h}}_j h^j是生成的假节点(边缘分布的乘积)时, ( h ^ ⃗ j , s ⃗ ) (\vec{\hat{h}}_j, \vec{s}) (h^j,s)是负样本。
判别器 D \mathcal{D} D是一个双线性层:
在本文的问题中,基于Jensen-Shannon散度和互信息间的进行的单调关系,就可以使用针对判别器 D \mathcal{D} D的二元交叉熵损失,最大化互信息:
本质上判别器是用于最大化高阶的全局表示和局部表示(节点级别)之间的互信息,这可以使编码器学习到所有全局相关位置的信息。
(2)负样本生成器
负样本集 { [ h ⃗ m , s ⃗ ] } m = 1 M {\{[\vec{h}_m, \vec{s}]}\}^M_{m=1} {[hm,s]}m=1M由不存在于异质图中的节点组成。作者将[1]中的负样本生成过程扩展到异质图。负样本生成器如下:
负样本生成器保持所有的基于元路径的邻接矩阵不变,保持 G \mathcal{G} G整体结构的稳定性。打乱节点特征矩阵 X X X的行,图的结构并没有变,但是每个节点对应的初始的特征向量变了,如图3所示。
5 实验
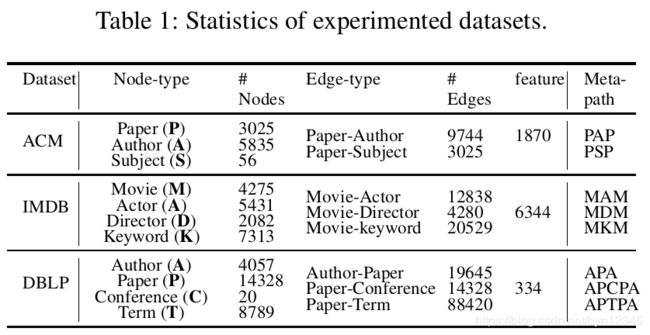
数据集:DBLP, ACM, IMDB
实验任务:节点分类,节点聚类
对比方法:
(1)无监督方法
- Raw Feature:初始特征作为嵌入表示
- Metapath2vec
- DeepWalk
- DeepWalk+Raw
- DGI[1]
- HDGI-C:使用GCN捕获局部特征
- HDGI-A:使用attention机制学习局部特征
(2)有监督方法
- GCN
- RGCN
- GAT
- HAN
实验结果:
(1)节点分类实验结果
(2)节点聚类实验结果
6 总结
本文提出一个无监督的GNN——HDGI,用于异质图的节点表示学习。
HDGI使用卷积形式的GNN和语义级别的attention机制,捕获节点的局部表示信息。
通过最大化local-global互信息,HDGI学习到了包含graph-level结构信息的high-level表示。并使用了元路径建模异质图中的语义关联。
HDGI在节点分类和节点聚类任务上表现出了很好的效果,在节点分类任务上甚至比有监督的方法表现还好。
最大化互信息是无监督表示学习很有潜力的一个方向。
本文的亮点在于将最大化局部和全局的互信息引入到优化目标中,是DGI(Deep Graph Infomax)向异质图的扩展。
流程大致分为以下几步:
(1)先针对特定的元路径进行节点级别的编码,这一过程使用GCN / GAT;
(2)然后使用语义级别的attention,聚合(1)得到的不同元路径的信息(受HAN的启发),这一步结束后得到局部信息;
(3)将(2)的输出作为输入,编码得到全局信息;
(4)HDGI的学习:基于互信息的判别器,负样本的生成
文章的4.4部分是重点,讲解了损失函数是怎么得来的,我还不是很理解。
这里有两篇文章,一篇讲解了DGI,一篇是对深度学习中的互信息的讲解。再多找点资料理解理解吧。
DEEP GRAPH INFOMAX 阅读笔记
深度学习中的互信息:无监督提取特征
参考文献
[1] Petar Velickovi´c, William Fedus, William L Hamilton, Pietro Lio, Yoshua Bengio, and R Devon Hjelm. Deep graph infomax. International Conference on Learning Representation, 2019.
[2] Manjunath Kudlur Oriol Vinyals, Samy Bengio. Order matters:
Sequence to sequence for sets. In International Conference on Learning Representation, 2016
[3] Mohamed Ishmael Belghazi, Aristide Baratin, Sai Rajeswar, Sherjil Ozair, Yoshua Bengio, Aaron Courville, and R Devon Hjelm. Mine: mutual information neural estimation. ICML, 2018




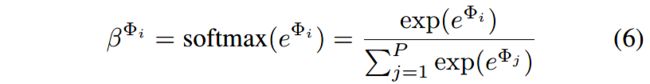

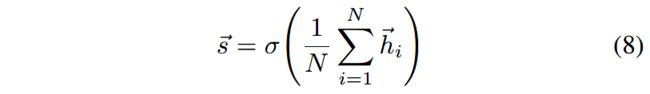
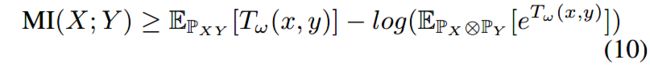
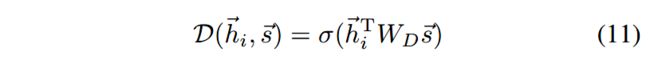

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lr8eSqah-1585216050847)(C:/Users/byn/AppData/Roaming/Typora/typora-user-images/image-20200326170454299.png)]](http://img.e-com-net.com/image/info8/36ba75c82a5b4c3b9b8215eec6b2eb43.jpg)