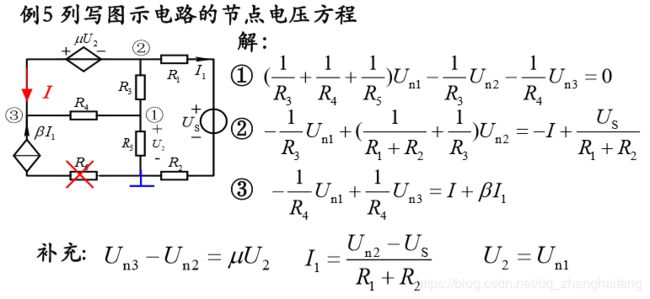
电路(第三章、线性直流电路一般分析方法)

1.线性直流电路的一般分析方法

1). 支路电流法

2). 回路电流法

3). 节点电压法

1). 支路电流法
a. 2b法，对于一个具有n个节点，b条支路的电路独立方程个数
KCL：n-1
KVL：b-n+1
支路方程：b
上述方程可以解出所有电压电流。
b.支路电流法
设给定的线性直流电路具有b条支路，n个节点，那么支路电流法就是以b个未知的支路电流作为待求量，对n-1个节点列出独立的KCL方程，在对b-n+1个回路列出独立的KVL方程，这b个方程联立便可解得b个支路电流。
$关键：独立方程的列写$
$KCL方程：n-1$
$KVL方程：b-n+1(选网孔，网孔数等于独立方程数)$、

2). 回路电流法
a.回路电流：假设在每个独立回路中闭合流动的电流。
b.回路电流法：以回路电流作为待求量，对b-n+1个回路列写KVL方程的方法。
c.列些规则：如上图
$$R_{11}{I}_{m1}+R_{12}{I}_{m2}+R_{13}{I}_{m3}=\sum _{回路1}{U}_s$$
$$R_{21}{I}_{m1}+R_{22}{I}_{m2}+R_{23}{I}_{m3}=\sum _{回路2}{U}_s$$
$$R_{31}{I}_{m1}+R_{32}{I}_{m2}+R_{33}{I}_{m3}=\sum _{回路3}{U}_s$$
(1).$R_{11}=R_1+R_4+R_5,R_{22}=R_2+R_5+R_6,R_{33}=R_3+R_4+R_6$表示组成回路$I_{m1},I_{m2},I_{m3}$的各支路上电阻之和，称为回路的自阻。

(2).$R_{12}=R_{21}=R_5,R_{13}=R_{31}=-R_4,R_{23}=R_{32}=R_6$表示两个回路之间的互阻$(公共支路)$。如果这两个回路电流在此公告支路上方向相同，互阻为正，否则为负。

(3).$\sum _{回路}=U_s$,表示沿回路$I_{m1},I_{m2},I_{m3}$电压源电位升的代数和，$沿回路电位升取正，沿回路电位降取负$。
$个人见解，我认为回路电流法，其实就是用独立电流来列写KVL方程。$

3). 节点电压法
a.节点电压：任选一节点作为参考点，其他节点与参考点之间的电压称为该点的节点电压。(节点电压具有单值性，与路径无关)
b.节点电压法：以n-1个节点电压为待求量，对n-1个节点列写KCL方程的方法。

以上图为例
方法：
1.节点③为参考，①、②节点列写KCL方程。
$$I_1+I_2+I_3+I_4=I_{S1}$$
$$-I_3-I_4+I_5=-I_{S5}$$
2.用节点电压表示支路电流：
①：$$\frac{U_{n1}}{R_1}+\frac{U_{n1}-U_{S2}}{R_2}+\frac{U_{n1}-U_{n2}+U_{S3}}{R_3}+\frac{U_{n1}-U_{n2}}{R_4}=I_{S1}$$
②：$$-\frac{U_{n1}-U_{n2}+U_{S3}}{R_3}-\frac{U_{n1}-U_{S2}}{R_4}+\frac{U_{n2}}{R_5}=-I_{S5}$$
整理得：
$$G_{11}{U}_{n1}-G_{12}{U}_{n2}=\sum _{节点1}{I}_{sk}+\sum _{节点1}{G}_k{U}_{sk}$$
$$-G_{21}{U}_{n1}+G_{22}{U}_{n2}=\sum _{节点2}{I}_{sk}+\sum _{节点2}{G}_k{U}_{sk}$$
列些规则：
$G_{11}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4},G_{22}=\frac{1}{R_3}+\frac{1}{R_4}+\frac{1}{R_5}$ 称为节点①、②的自导。
$G_{12}=-(\frac{1}{R_3}+\frac{1}{R_4}),G_{21}=-(\frac{1}{R_3}+\frac{1}{R_4})$ 称为节点①、②间的互导。
$\sum _{节点1}{I}_{sk},\sum _{节点2}{I}_{sk}$表示节点相连的电流源的电流代数和。
$\sum _{节点1}{G}_k{U}_{sk}，\sum _{节点2}{G}_k{U}_{sk}$表示与节点相连电压源于电导的乘积之和。$正负看正极与负极那个离得近$

3.运算放大器
运算放大器，简称运放，是一种集成电路工艺制造的多端元件。
运算放大器的端口方程：$u=A(u_b-u_0)$

$运算放大器存在"虚断"：i_n=i_p;"虚短":v_p=v_n$