对LCA、树上倍增、树链剖分（重链剖分&长链剖分）和LCT（Link-Cut Tree）的学习

LCA

---

what is LCA & what can LCA do

LCA（Lowest Common Ancestors），即最近公共祖先
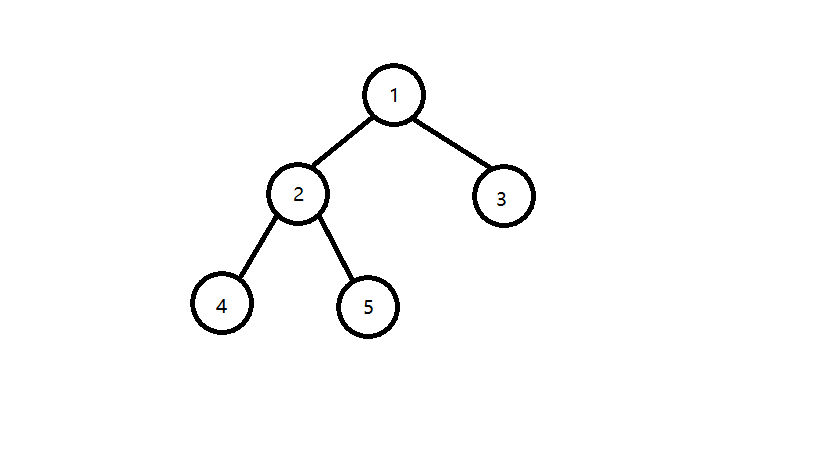
在一棵树上，两个节点的深度最浅的公共祖先就是$LCA$ （自己可以是自己的祖先）
很简单，我们可以快速地进入正题了

下图中的树，$4$和$5$的$LCA$为2，$1$和$3$的$LCA$是1（1也算1的祖先）

除了是直接求两点的$LCA$的模板题，没有题目会叫你打个模板

那么LCA能干嘛？

其实$LCA$的用途很广，感觉用$LCA$最多的像是这样子的题

• 给你一棵树 （或者是一个图求完MST，这很常见） 和树上的两点

• 然后找出这两点之间的路径的极值或权值和或其他东东

这时我们可以借助这两点的LCA作为中转点来轻松地解决这类题目

---

how to discover LCA

还是这棵树

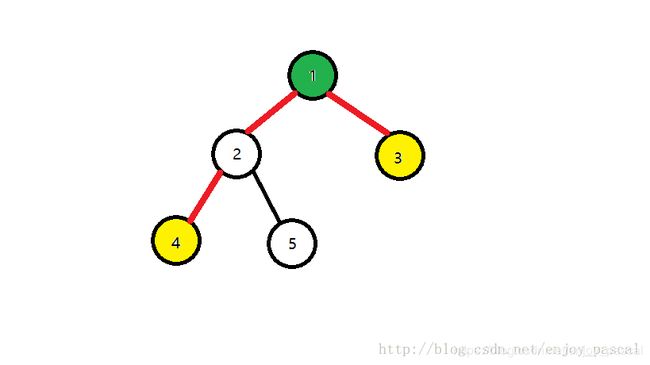
$4$和$3$的$LCA$是1，这两点间的路径是下图标红的路径

怎么求LCA呢？

---

method one

暴力dfs一遍，时间复杂度$O(n)$
侮辱智商
（逃）

---

method two

模拟，从两点开始一起向上跳一步，跳过的点标记一下，时间复杂度$O(n)$
侮辱智商*2
（逃）

---

method three

用dfs记录每个点的深度，求$LCA$时先调至统一深度，再一起向上跳
如果这棵树是一个刚好分成两叉的树，时间复杂度$O(n)$
侮辱智商*3
（逃）

---

上面的都是小学生都会的东西，不必讲了
想真正用有意义的$LCA$，下面才是重点

---

tarjan算法（离线）求LCA

求$LCA$有一种非常容易理解的方法就是tarjan算法预处理离线解决，时间复杂度$O(n+q)$，飞速

仍感觉离线算法不适用于所有题目
（比如某些良心出题人丧病地要你强制在线，GG）

反正在线算法可以解决离线能做出来所有的题

所以，我不讲$tarjan$求$LCA$了，推荐一篇写的很棒的blog
接下来的几个在线算法才是搞$LCA$的门槛

---

ST（RMQ）算法（在线）求LCA

这种方法的思想，就是将LCA问题转化成RMQ问题

• 如果不会$RMQ$问题——$ST$算法的就戳这里吧

---

可以转化成RMQ问题？

这里有棵树

如何预处理呢？

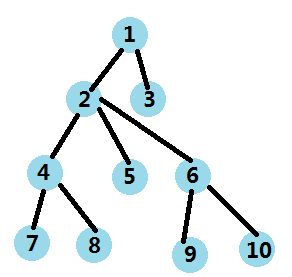
我们用dfs遍历一次，得到一个$dfs$序（儿子节点回到父亲节点还要再算一遍）
$dfs$序就是这样的1->2->4->7->4->8->4->2->5->2->6->9->6->10->6->2->1->3->1
（一开始在$root$向儿子节点走，到了叶子节点就向另一个儿子走，最后回到$root$）

$dfs$预处理的时间复杂度为$O(n)$

---

dfs序妙啊

设$r[x]$表示$x$在$dfs$序当中第一次出现的位置，$depth[x]$表示$x$的深度
如果求$x$和$y$的$LCA$，r[x]~r[y]这一段区间内一定有$LCA(x,y)$，而且一定是区间中深度最小的那个点

（比如上面的dfs序中，第一个$7$和第一个$5$之间的序列里的深度最小的点是$2$，而$2$正是$7$和$5$的$LCA$！）

• 遍历以$LCA(x,y)$为根的树时，不遍历完所有以$LCA(x,y)$为根的树的节点是不会回到$LCA(x,y)$的

• 还有就是明显地，想到达x再到y，必须上溯经过它们的LCA（两个点之间有且只有一条路径）

• 所以$LCA$的深度一定最小

直接用RMQ——ST表维护这个东西，求出来的最小值的点即为$LCA$

---

matters need attention

• $dfs$序的长度是$2n-1$，用$dfsO(n)$处理出$r$、$depth$和$dfs$序之后直接套上裸的$RMQ$

• 设$f[i][j]$表示dfs序中j~j+2^i-1的点当中，depth值最小的是哪个点 即可

• 那么单次询问时间复杂度$O(1)$

• 完美

---

code

这段代码是我co过来的，因为我也是看别人博客学的
但这代码是真的丑

#include 
#include 
#include 

using namespace std;

int n,_n,m,s;//_n是用来放元素进dfs序里，最终_n=2n-1

struct EDGE
{
    int to;
    EDGE* las;
}e[1000001];//前向星存边

EDGE* last[500001];
int sx[1000001];//顺序，为dfs序
int f[21][1000001];//用于ST算法
int deep[500001];//深度
int r[500001];//第一次出现的位置

int min(int x,int y)
{
	return deep[x]<deep[y]?x:y;
}

void dfs(int t,int fa,int de)
{
    sx[++_n]=t;
    r[t]=_n;
    deep[t]=de;
    EDGE*ei;
    for (ei=last[t];ei;ei=ei->las)
        if (ei->to!=fa)
        {
            dfs(ei->to,t,de+1);
            sx[++_n]=t;
        }
}

int query(int l,int r)
{
    if (l>r)
    {
    	//交换 
        l^=r;
        r^=l;
        l^=r;
    }
    int k=int(log2(r-l+1));
    return min(f[k][l],f[k][r-(1<<k)+1]);
}

int main()
{
    scanf("%d%d%d",&n,&m,&s);
    int j=0,x,y;
    for (int i=1;i<n;++i)
    {
        scanf("%d%d",&x,&y);
        e[++j]={y,last[x]};
        last[x]=e+j;
        e[++j]={x,last[y]};
        last[y]=e+j;
    }
    dfs(s,0,0);
    //以下是ST算法
    for (int i=1;i<=_n;++i)f[0][i]=sx[i];
    int ni=int(log2(_n)),nj,tmp;
    for (int i=1;i<=ni;++i)
    {
        nj=_n+1-(1<<i);
        tmp=1<<i-1;
        for (j=1;j<=nj;++j)
            f[i][j]=min(f[i-1][j],f[i-1][j+tmp]);
    }
    //以下是询问，对于每次询问，可以O(1)回答
    while (m--)
    {
        scanf("%d%d",&x,&y);
        printf("%d\n",query(r[x],r[y]));
    }
}

---

小结

基础的$LCA$知识你应该已经会了吧
$LCA$的运用挺广吧，感觉和线段树的考频有的一比，不掌握是会吃亏的
上面的是比较普通的方法求$LCA$，其实树上倍增也能求$LCA$
接下来到丧心病狂 （其实很简单） 的树上倍增了

---

树上倍增

---

又是什么东东？

倍增这个东东严格来说就是种思想，只可意会不可言传
倍增，是根据已经得到了的信息，将考虑的范围扩大，从而加速操作的一种思想

使用了倍增思想的算法有

• 归并排序
• 快速幂
• 基于ST表的RMQ算法
• 树上倍增找LCA等
• FFT、后缀数组等高级算法

• ……$FFT$有倍增的么……我可能学了假的$FFT$

---

some advantages

树上倍增和$RMQ$是比较相似的，都采用了二进制的思想，所以时空复杂度低
其实树上倍增和树链剖分在树题里面都用的很多

• 两个都十分有趣，但倍增有着显而易见的优点——

• 比起树链剖分，树上倍增代码短，查错方便，时空复杂度优（都是$O(nlo{g}_{2}n)$）

• 只是功能欠缺了一些不要太在意

即使如此，树上倍增也能够解决大部分的树型题目反正两个都要学

---

树上倍增（在线）求LCA

preparation

怎么样预处理以达到在线单次询问$O(lo{g}_{2}n)$的时间呢？

我们需要构造倍增数组

• 设$anc[i][j]$表示i节点的第2^j个祖先

• 注意$anc$数组开到$anc[n][lo{g}_{2}n]$，因为树上任意一点最多有$2^{lo{g}_{2}n}$个祖先

• 可以发现这个东西可以代替不路径压缩的并查集，$\because anc[i][0]=father(i)$
  （若$anc[i][j]=0$则说明$i$的第$2^j$祖先不存在）

然后，倍增的性质 （DP方程） 就清楚地出来了$$anc[i][j]=anc[anc[i][j-1]][j-1]$$

• 用文字来表达它就是这样的

• i的第$2^j$个父亲是i的第$2^{j-1}$个父亲的第$2^{j-1}$个父亲

• 神奇不？

就是说暴力求$i$的第$k$个祖先的时间复杂度是$O(k)$，现在变成了$O(lo{g}_{2}k)$
同时，用一个dfs处理出每个点的深度$depth[x]$和$anc[x][0]$，时间复杂度$O(n)$
预处理的时间复杂度即为$O(n{\log }_{2}n)$

---

code

procedure dfs(x,y:longint);
var
        now:longint;
begin
        now:=last[x];
        while now<>0 do
        begin
                if b[now]<>y then
                begin
                        anc[b[now],0]:=x;
                        depth[b[now]]:=depth[x]+1;
                        dfs(b[now],x);
                end;
                now:=next[now];
        end;
end;

		for j:=1 to trunc(ln(n)/ln(2)) do
        for i:=1 to n do
                anc[i,j]:=anc[anc[i,j-1],j-1];

---

query

请务必认认真真地阅读以下内容否则树上倍增你就学不会了

树上倍增的运用中，最简单最实用的就是求$LCA$了

• 现在我们需要求出$LCA(x,y)$，怎么倍增做？

还记得前面三种脑残 $O(n)$求$LCA$的第三个方法吗？

用dfs记录每个点的深度，求LCA时先调至统一深度，再一起向上跳

其实树上倍增运用的就是这个思想！只不过时间复杂度降至了飞快的$O({\log }_{2}n)$

• 对于两个节点$u$和$v$，我们先把$u$和$v$调至同一深度

• 若此时$u=v$，那么原来两点的$LCA$即为当前点

• 如果$depth[u]=depth[v]$但$u̸=v$，就说明$LCA(u,v)$在更浅的地方

• 我们同时把$u$和$v$向上跳$2^k$步（$k=lo{g}_{2}depth[u]$），直到$u=v$

明显这种方法肯定能求出$LCA$，因为$u$和$v$一定会相遇
倍增比那种脑残方法优的是，脑残方法一步一步向上跳，倍增一次跳$2^k$步！

• 但还存在着一些问题——如果这样跳，跳到了$LCA$的祖先节点怎么搞？

所以如果$u$和$v$向上跳$2^k$步到达的节点相同，那我们就不跳，让$u$和$v$的第$2^k$祖先不同即可跳
注意每下一次向上跳的距离是上一次跳的$\frac{1}{2}$（$k=k-1$），直到$u=v$，$LCA$即已被求出

这样使$u$和$v$与$LCA$的距离每次缩短一半，时间复杂度也就是$O({\log }_{2}n)$的

最后如何把$u$和$v$调至同一深度？
其实是一样的，先把较深的那个点调浅就行了

---

code

• 觉得上面说得抽象的话见标理解一下

function lca(x,y:longint):longint;
var
        k:longint;
begin
        if depth[x]<depth[y] then swap(x,y);
        k:=trunc(ln(depth[x]-depth[y]+1)/ln(2));
        while k>=0 do
        begin
                if depth[anc[x,k]]>depth[y] then x:=anc[x,k];
                dec(k);
        end;
        if depth[x]<>depth[y] then x:=anc[x,0];
        k:=trunc(ln(d[x])/ln(2));
        while k>=0 do
        begin
                if anc[x,k]<>anc[y,k] then
                begin
                        x:=anc[x,k];
                        y:=anc[y,k];
                end;
                dec(k);
        end;
        exit(x);
end;

以上三段$code$已经能解决树上倍增求$LCA$了
树上倍增求$LCA$的时间复杂度为$O(n{\log }_{2}n+q{\log }_{2}n)$

---

树上倍增的真正意义

比赛里面直接求$LCA$是没有什么用处的
其实，树上倍增的真正可怕之处是这个倍增的思想

• 不信？ 来看看这种很常见的题目

给你一棵树和两个点$x$和$y$，求这两点间路径的路径最大/小的点权/边权

明显我们要先求$x$和$y$的$LCA$，因为唯一路径必须经过$LCA$
求$LCA$比如说用$RMQ$，然后呢？暴力$O(n)$再遍历一次路径？
不可能的

• 这种问题用树上倍增还是能用$O({\log }_{2}n)$的时间解决

• 我们可以设$dis[i][j]$表示i到他的第$2^j$个祖先的路径最大值，就可以边求$LCA$边顺便求出两点距离

• 因为$dis$也符合
  $$dis[i][j]=max(dis[i][j-1],dis[anc[i][j-1]][j-1])$$

还有求两点的路径上路径权值和呢？

• 设$sum[i][j]$表示i到他的第$2^j$个祖先的路径权值和，同时也可边求$LCA$边求和，因为
  $$sum[i][j]=sum[i][j-1]+sum[anc[i][j-1]][j-1])$$

这才是树上倍增的真正意义所在，像$RMQ$求$LCA$，是无法解决这类问题的
至此树上倍增讲的差不多了，看例题

---

例题1：【JZOJ1738】Heatwave

problem

Description 给你N个点的无向连通图，图中有M条边，第j条边的长度为： d_j. 　　现在有 K个询问。 　　每个询问的格式是：A
B，表示询问从A点走到B点的所有路径中，最长的边最小值是多少？

Input

文件名为heatwave.in 　　第一行： N, M, K。 　　第2…M+1行: 三个正整数：X, Y, and D (1 <=
X <=N; 1 <= Y <= N). 表示X与Y之间有一条长度为D的边。 　　第M+2…M+K+1行: 每行两个整数A
B,表示询问从A点走到B点的所有路径中，最长的边最小值是多少？

Output

对每个询问，输出最长的边最小值是多少。

Sample Input

6 6 8 1 2 5 2 3 4 3 4 3 1 4 8 2 5 7 4 6 2 1 2 1 3 1 4 2 3 2 4 5 1 6 2
6 1

Sample Output

5 5 5 4 4 7 4 5

Data Constraint

50% 1<=N,M<=3000 其中30% K<=5000 ​100% 1 <= N <= 15,000 　　1 <= M <=
30,000 　　1 <= d_j <= 1,000,000,000 　　1 <= K <= 20,000

Hint

---

think about other issues

先不考虑其他的，先考虑一下如何搞定题目所给的问题
注意这句话——

从A点走到B点的所有路径中，最长的边的最小值是多少？

想到什么了吗？

• MST！ 既然让最长的边最短，那么我们就求这棵树的最小生成树即可

这样就可以保证两点间最长边最短 ，这里直接用kruskal+并查集艹过去就行了
用邻接表存下即可

---

analysis

• 求完$MST$后，这道题是不是就是道裸题？维护$anc[i][j]$和$dis[i][j]$即可
  照样用一个$dfs$遍历整棵树，维护出$depth[x]$、$anc[x][0]$和$dis[x][0]$，之后$O(n{\log }_{2}n)$预处理

• 搞定之后，我们对每一对$(u,v)$求$LCA$（设$u$深度更深）注意求$LCA$过程中记录每一次的max值即
  $$ans=max(di{s}_{u,k})$$

• $ans$即为答案

时间复杂度为$O(mlo{g}_{2}m+nlo{g}_{2}n+qlo{g}_{2}n)$我乱算的

---

code

var
        b,c,next,last,father,depth:array[0..50000]of longint;
        anc,dis:array[0..15000,0..16]of longint;
        a:array[0..30000,0..3]of longint;
        n,m,q,i,j,x,y,tot:longint;

procedure swap(var x,y:longint);
var
        z:longint;
begin
        z:=x;
        x:=y;
        y:=z;
end;

function max(x,y:longint):longint;
begin
        if x>y then exit(x);
        exit(y);
end;

procedure qsort(l,r:longint);
var
        i,j,mid:longint;
begin
        i:=l;
        j:=r;
        mid:=a[(l+r)div 2,3];
        repeat
                while a[i,3]<mid do inc(i);
                while a[j,3]>mid do dec(j);
                if i<=j then
                begin
                        a[0]:=a[i];
                        a[i]:=a[j];
                        a[j]:=a[0];
                        inc(i);
                        dec(j);
                end;
        until i>j;
        if l<j then qsort(l,j);
        if i<r then qsort(i,r);
end;

function getfather(x:longint):longint;
begin
        if father[x]=x then exit(x);
        father[x]:=getfather(father[x]);
        exit(father[x]);
end;

function judge(x,y:longint):boolean;
begin
        exit(getfather(x)=getfather(y));
end;

procedure insert(x,y,z:longint);
begin
        inc(tot);
        b[tot]:=y;
        next[tot]:=last[x];
        last[x]:=tot;
        c[tot]:=z;
end;

procedure dfs(x,y:longint);
var
        now:longint;
begin
        now:=last[x];
        while now<>0 do
        begin
                if b[now]<>y then
                begin
                        anc[b[now],0]:=x;
                        depth[b[now]]:=depth[x]+1;
                        dis[b[now],0]:=c[now];
                        dfs(b[now],x);
                end;
                now:=next[now];
        end;
end;

function lca(x,y:longint):longint;
var
        k:longint;
begin
        lca:=0;
        if depth[x]<depth[y] then swap(x,y);
        k:=trunc(ln(depth[x]-depth[y]+1)/ln(2));
        while k>=0 do
        begin
                if depth[anc[x,k]]>depth[y] then
                begin
                        lca:=max(lca,dis[x,k]);
                        x:=anc[x,k];
                end;
                dec(k);
        end;
        if depth[x]<>depth[y] then
        begin
                lca:=max(lca,dis[x,0]);
                x:=anc[x,0];
        end;
        k:=trunc(ln(depth[x])/ln(2));
        while k>=0 do
        begin
                if anc[x,k]<>anc[y,k] then
                begin
                        lca:=max(max(lca,dis[x,k]),dis[y,k]);
                        x:=anc[x,k];
                        y:=anc[y,k];
                end;
                dec(k);
        end;
        if x=y then exit(lca);
        exit(max(lca,max(dis[x,0],dis[y,0])));
end;

begin                                             
        readln(n,m,q);
        for i:=1 to n do father[i]:=i;
        for i:=1 to m do readln(a[i,1],a[i,2],a[i,3]);
        qsort(1,m);
        for i:=1 to m do
        begin
                if (not judge(a[i,1],a[i,2])) then
                begin
                        insert(a[i,1],a[i,2],a[i,3]);
                        insert(a[i,2],a[i,1],a[i,3]);
                        father[getfather(a[i,1])]:=getfather(a[i,2]);
                end;
        end;
        depth[1]:=1;
        dfs(1,0);
        for j:=1 to trunc(ln(n)/ln(2)) do
        for i:=1 to n do
        begin
                anc[i,j]:=anc[anc[i,j-1],j-1];
                dis[i,j]:=max(dis[i,j-1],dis[anc[i,j-1],j-1]);
        end;
        for i:=1 to q do
        begin
                readln(x,y);
                writeln(lca(x,y));
        end;
end.

---

例题2：【JZOJ2753】树（tree）

problem

Description

   在这个问题中，给定一个值S和一棵树。在树的每个节点有一个正整数，问有多少条路径的节点总和达到S。路径中节点的深度必须是升序的。假设节点1是根节点，根的深度是0，它的儿子节点的深度为1。路径不必一定从根节点开始。

Input

   第一行是两个整数N和S，其中N是树的节点数。


   第二行是N个正整数，第i个整数表示节点i的正整数。


   接下来的N-1行每行是2个整数x和y，表示y是x的儿子。

Output

   输出路径节点总和为S的路径数量。

Sample Input

3 3 1 2 3 1 2 1 3

Sample Output

2

Data Constraint

Hint

对于30%数据，N≤100；

对于60%数据，N≤1000；

对于100%数据，N≤100000，所有权值以及S都不超过1000。

---

analysis

相信这题应该难不住你了吧
正解即为树上倍增+二分

首先还是一样，用$O(n{\log }_{2}n)$的时间预处理$anc$数组
至于权值，你可以顺便维护$dis$数组，但为何不用简单的前缀和呢？
剩下来的就比较简单啦

• 枚举节点$i$，二分一个$mid$表示$i$的第$mid$个祖先

• 然后通过$anc$数组用$O({\log }_{2}n)$的时间求出$i$的第$mid$个祖先是哪个节点 （设为是第$k$号）

• 若$pre[i]-pre[k]>s$则$right=mid-1$，$pre[i]-pre[k]<s$则$left=mid+1$
  $=s$就刚好找到了

• 此时累加答案即可

时间复杂度为$O(n{\log }_2^{2}n)$

---

code

#include
#define MAXN 100001

using namespace std;

int last[MAXN],next[MAXN],tov[MAXN];
int a[MAXN],value[MAXN],depth[MAXN];
int f[MAXN][21];
int n,s,tot,ans;

void insert(int x,int y)
{
	next[++tot]=last[x];
	last[x]=tot;
	tov[tot]=y;
}

void dfs(int x)
{
	for (int i=last[x];i;i=next[i])
	{
		int j=tov[i];
		value[j]=value[x]+a[j];
		f[j][0]=x;
		depth[j]=depth[x]+1;
		dfs(j);
	}
}

int find(int x,int k)
{
	int t=0;
	while (k)
	{
		if(k&1)x=f[x][t];
		t++;k/=2;
	}
	return x;
}

bool judge(int x)
{
	int left=0,right=depth[x];
	while (left<=right)
	{
		int mid=(left+right)/2,temp=find(x,mid);
		if (value[x]-value[temp]==s) 
		{
			return 1;
		}
		else 
		{
			if (value[x]-value[temp]>s)
			{
				right=mid-1;
			}
			else 
			{
				left=mid+1;
			}
		}
	}
	return 0;
}

int main()
{
	scanf("%d%d",&n,&s);
	for (int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
	}
	for (int i=1;i<n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		insert(x,y);
	}
	depth[1]=1,value[1]=a[1];
	dfs(1);
	for (int j=1;j<=floor(log(n)/log(2));j++)
	{
		for (int i=1;i<=n;i++)
		{
			f[i][j]=f[f[i][j-1]][j-1];
		}
	}
	for (int i=1;i<=n;i++)
	{
		if (judge(i))ans++;
	}
	printf("%d\n",ans);
	return 0;
}

---

例题3：【JZOJ5966】【NOIP2018】保卫王国

problem

Description Z国有n座城市，n-1条双向道路，每条双向道路连接两座城市，且任意两座城市都能通过若干条道路相互到达。
Z国的国防部长小Z要在城市中驻扎军队。驻扎军队需要满足如下几个条件： ①一座城市可以驻扎一支军队，也可以不驻扎军队。
②由道路直接连接的两座城市中至少要有一座城市驻扎军队。 ③在城市里驻扎军队会产生花费，在编号为i的城市中驻扎军队的花费是pi。
小Z很快就规划出了一种驻扎军队的方案，使总花费最小。但是国王又给小Z提出了m个要求，每个要求规定了其中两座城市是否驻扎军队。小Z需要针对每个要求逐一给出回答。具体而言，如果国王提出的第j个要求能够满足上述驻扎条件（不需要考虑第j个要求之外的其它要求），则需要给出在此要求前提下驻扎军队的最小开销。如果国王提出的第j个要求无法满足，则需要输出-1(1<=j<=m)
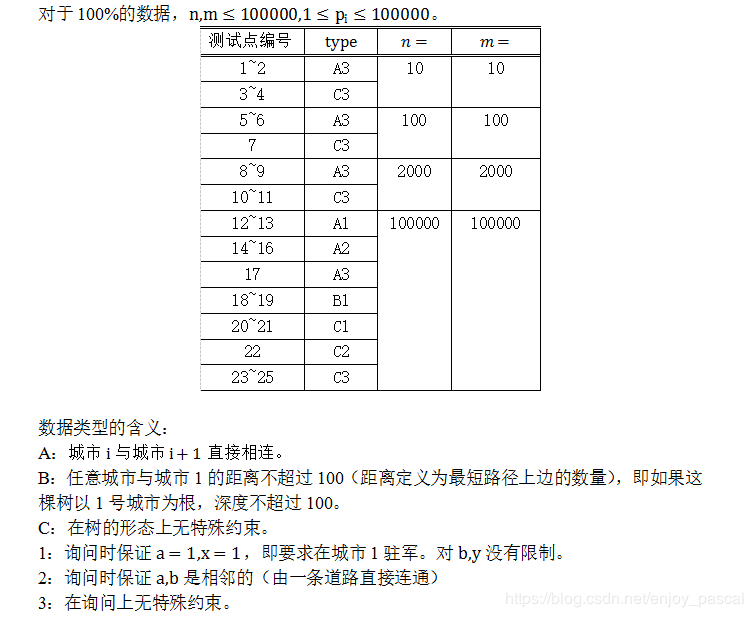
。现在请你来帮助小Z。

Input 输入文件名为defense.in。 第1行包含两个正整数n,m 和一个字符串type
，分别表示城市数、要求数和数据类型。type
是一个由大写字母A，B或C和一个数字1，2，3组成的字符串。它可以帮助你获得部分分。你可能不需要用到这个参数。这个参数的含义在【数据规模与约定】中有具体的描述。
第2 行n个整数pi ，表示编号i的城市中驻扎军队的花费。 接下来n-1行，每行两个正整数u,v ，表示有一条u 到v 的双向道路。 接下来
m行，第 j行四个整数a,x,b,y(a<>b)
，表示第j个要求是在城市a驻扎x支军队，在城市b驻扎y支军队。其中，x、y的取值只有0或1：若x为0，表示城市a不得驻扎军队，若x为1，表示城市a必须驻扎军队；若y为0，表示城市b不得驻扎军队，若y为1，表示城市b必须驻扎军队。
输入文件中每一行相邻的两个数据之间均用一个空格分隔。

Output 输出文件名为defense.out。 输出共
行，每行包含1个整数，第j行表示在满足国王第j个要求时的最小开销，如果无法满足国王的第j个要求，则该行输出-1。

Sample Input 输入1： 5 3 C3 2 4 1 3 9 1 5 5 2 5 3 3 4 1 0 3 0 2 1 3 1 1 0
5 0

Sample Output 输出1： 12 7
-1 【样例解释】 对于第一个要求，在4号和5号城市驻扎军队时开销最小。 对于第二个要求，在1号、2号、3号城市驻扎军队时开销最小。 第三个要求是无法满足的，因为在1号、5号城市都不驻扎军队就意味着由道路直接连接的两座城市中都没有驻扎军队。

Data Constraint

---

analysis

• 正解倍增+矩乘+树形DP

• 考虑一下$44pts$的树形$DP$，设$f[i][0/1]$表示以$i$为根的子树中，$i$选或不选的最优解，则
  $$f[i][0]=\sum f[son][1]$$$$f[i][1]=\sum min(f[son][0],f[son][1])$$

• 每次把某个$f$赋值为$\infty$，暴力重新$DP$，就可以得到$44pts$的好成绩

• 接着考虑另一个$DP$，设$g[i][0/1]$表示以$i$为根的子树外，$i$选或不选的最优解

• 由于我们已经$DP$出了$f$数组，我们也可以从一个点的父亲来转移$g$，则
  $$g[i][0]=f[i][0]+g[fa][1]-min(f[i][0],f[i][1])$$$$g[i][1]=f[i][1]+min(g[fa][0]-f[i][1],g[fa][1]-min(f[i][0],f[i][1]))$$

• 这个$DP$也满好理解的，接下来是维护的问题

• 注意到其实没有数据更改，那么我们可以用倍增+矩乘的方法来求出一条链上的答案

• 设$dis[i][x][0/1][0/1]$表示$i$选或不选且$i$的$2^x$位祖先选或不选的最优解，则

$$dis[i][0][0][0]=\infty$$$$dis[i][0][1][0]=f[fa][0]-f[i][1]$$$$dis[i][0][0][1]=dis[i][0][1][1]=f[fa][1]-min(f[i][0],f[i][1])$$

• 这个应该不难理解，$i$和父亲不能都不选，所以是$\infty$

• 其他的都是用父亲的贡献减去儿子的贡献，应该不太难想

• 而把$dis$数组维护出来以后，就可以实现倍增了，用矩乘解决$dis$的后两维

• 注意倍增时的矩乘和平时的不太一样，修改一下才可以

• 对于每一个询问，如果两个点在一条链上，注意一下条件选或不选的判断就行了

• 否则找出两点的$LCA$，再倍增跳到$LCA$，计算两种不同情况的最优解即可

• 用$g$减去所求的东西才是最终的答案，不要忘记两个点的$LCA$选的时候有不同的情况需要取$min$

• 时间复杂度$O(n{\log }_{2}n)$

---

code

#pragma GCC optimize("O3")
#pragma G++ optimize("O3")
#include
#include
#include
#define MAXN 100005
#define MAXM MAXN*2
#define ll long long
#define reg register ll
#define INF 1000000000000000007ll
#define fo(i,a,b) for (reg i=a;i<=b;++i)
#define fd(i,a,b) for (reg i=a;i>=b;--i)
#define rep(i,a) for (reg i=last[a];i;i=next[i])
#define O3 __attribute__((optimize("-O3")))

ll last[MAXM],next[MAXM],tov[MAXM];
ll p[MAXN],depth[MAXN],fa[MAXN];
ll f[MAXN][2],g[MAXN][2];
ll anc[MAXN][21];
ll n,m,tot,ans;
char type[5];

struct node
{
	ll a[2][2];
}dis[MAXN][21],A,B,C;

O3 inline ll read()
{
	ll x=0,f=1;char ch=getchar();
	while (ch<'0' || '9'<ch){if (ch=='-')f=-1;ch=getchar();}
	while ('0'<=ch && ch<='9')x=x*10+ch-'0',ch=getchar();
	return x*f;
}
O3 inline ll min(ll x,ll y)
{
	return x<y?x:y;
}
O3 inline void swap(ll &x,ll &y)
{
	x=x+y,y=x-y,x=x-y;
}
O3 inline void link(ll x,ll y)
{
	next[++tot]=last[x],last[x]=tot,tov[tot]=y;
}
O3 inline void dfs1(ll x)
{
	depth[x]=depth[fa[x]]+1,anc[x][0]=fa[x];
	fo(i,1,20)anc[x][i]=anc[anc[x][i-1]][i-1];
	f[x][0]=0,f[x][1]=p[x];
	rep(i,x)if (tov[i]!=fa[x])
	{
		fa[tov[i]]=x,dfs1(tov[i]);
		f[x][0]+=f[tov[i]][1];
		f[x][1]+=min(f[tov[i]][0],f[tov[i]][1]);
	}
}
O3 inline void dfs2(ll x)
{
	if (x==1)g[x][0]=f[x][0],g[x][1]=f[x][1];
	else
	{
		g[x][0]=f[x][0]+g[fa[x]][1]-min(f[x][0],f[x][1]);
		g[x][1]=f[x][1]+min(g[fa[x]][0]-f[x][1],g[fa[x]][1]-min(f[x][0],f[x][1]));
	}
	rep(i,x)if (tov[i]!=fa[x])
	{
		dis[tov[i]][0].a[0][0]=INF;
		dis[tov[i]][0].a[1][0]=f[x][0]-f[tov[i]][1];
		dis[tov[i]][0].a[0][1]=f[x][1]-min(f[tov[i]][0],f[tov[i]][1]);
		dis[tov[i]][0].a[1][1]=f[x][1]-min(f[tov[i]][0],f[tov[i]][1]);
		dfs2(tov[i]);
	}
}
O3 inline node merge(node A,node B)
{
	memset(C.a,60,sizeof(C.a));
	fo(i,0,1)fo(j,0,1)fo(k,0,1)
	C.a[i][j]=min(C.a[i][j],A.a[i][k]+B.a[k][j]);
	return C;
}
O3 int main()
{
	freopen("defense.in","r",stdin);
	freopen("defense.out","w",stdout);
	//freopen("readin.txt","r",stdin);
	n=read(),m=read(),scanf("%s",&type);
	fo(i,1,n)p[i]=read();
	fo(i,1,n-1)
	{
		ll x=read(),y=read();
		link(x,y),link(y,x);
	}
	dfs1(1),dfs2(1);
	fo(j,1,20)fo(i,1,n)dis[i][j]=merge(dis[i][j-1],dis[anc[i][j-1]][j-1]);
	while (m--)
	{
		ll a=read(),x=read(),b=read(),y=read();
		if (x+y==0 && ((fa[a]==b) || (fa[b]==a)))
		{
			printf("-1\n");
			continue;
		}
		if (depth[a]<depth[b])swap(a,b),swap(x,y);
		memset(A.a,60,sizeof(A.a));
		memset(B.a,60,sizeof(B.a));
		A.a[x][x]=f[a][x],B.a[y][y]=f[b][y];
		fd(i,20,0)if (depth[anc[a][i]]>depth[b])
		{
			A=merge(A,dis[a][i]),a=anc[a][i];
		}
		if (fa[a]==b)
		{
			printf("%lld\n",y==0?g[b][0]-f[a][1]+A.a[x][1]:
			g[b][1]-min(f[a][0],f[a][1])+min(A.a[x][0],A.a[x][1]));
			continue;
		}
		if (depth[a]!=depth[b])A=merge(A,dis[a][0]),a=fa[a];
		fd(i,20,0)if (anc[a][i]!=anc[b][i])
		{
			A=merge(A,dis[a][i]),B=merge(B,dis[b][i]);
			a=anc[a][i],b=anc[b][i];
		}
		printf("%lld\n",min(g[fa[a]][0]-f[a][1]-f[b][1]+A.a[x][1]+B.a[y][1],
		g[fa[a]][1]-min(f[a][0],f[a][1])-min(f[b][0],f[b][1])+min(A.a[x][0],A.a[x][1])+min(B.a[y][0],B.a[y][1])));
	}
	return 0;
}

---

一些感想

树上倍增差不多算是那种一定要会的知识了
总之，这一种较为基础的算法，一定要熟练掌握并会运用它
（不要把正解看成暴力……）
接下来是丧心病狂 （其实比树上倍增还简单） 的树链剖分

---

树链剖分

---

介绍一下吧

零树剖基础的人，到这里应该还是不懂树剖的
简要地说一下吧——

• 树链剖分的思想是维护树上路径信息

• 树链剖分先通过轻重边剖分将树分为多条链，保证每个点属于且只属于一条链

• 然后再通过数据结构 （树状数组、SBT、splay、线段树等） 来维护每一条链

以上就是树链剖分的思想了，很少，学完以后，其实树剖很简单……
问题是怎么分轻重边？怎么维护？

---

more advantages

既然树上倍增又好打又好调，干嘛还用树链剖分？
但树上倍增的用途还就真没有树链剖分那么广
不信？ 再来一类看起来也很常见的题目

在一棵树上进行路径的权值修改，询问路径权值和、路径权值极值

看起来简单，但不简单，线段树、树上倍增根本做不了
why？ 后两个操作我们当然可以用树上倍增做
关键是修改操作，树上倍增都预处理好了

• 怎么修改？重新$O(n{\log }_{2}n)$暴力预处理？

不可能的

这时我们就要用树链剖分了
由于我们可以用数据结构来维护剖好的树，所以路径权值之类的当然是可以修改的
所以并不是说倍增就能真正完全通用

• 树剖的用处比倍增多，倍增能做的题树剖一定能做，反过来则否

• 树剖的代码复杂度不算特别高，调试也不难

• 在高级的比赛里，树剖是必备知识

其实树剖也是分类别的

• 注意树剖有三种：重链剖分、长链剖分和实虚链剖分

• 实虚链剖分其实就是LCT

• 所以我就分开来写好了

正式进入树链剖分的学习

---

重链剖分

请务必认认真真地阅读以下内容否则重链剖分你就学不会了

---

重链剖分的一些概念

轻儿子和重儿子

设$x_{size}$表示以x为根的子树的节点个数
对于每个非叶子节点y，y的儿子所有中$size$最大的儿子就是重儿子（两个或以上都最大的话，任意选一个）
而y其它的儿子，都是轻儿子
（轻儿子通常没有用，我们可以不去考虑它）

---

重边、轻边和重链

重儿子与其父亲之间的路径，就是重边
不是重边的边均为轻边
多条重边相连为一条重链

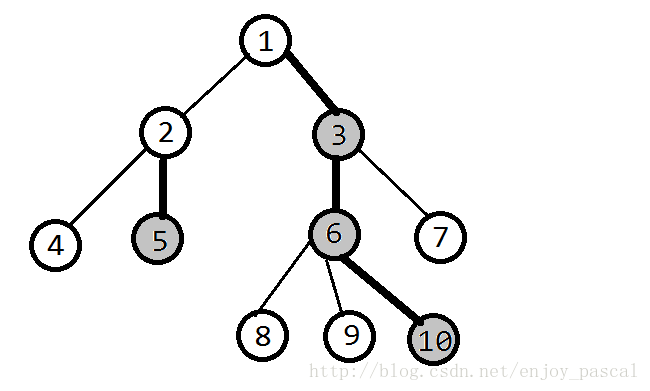
图中灰色的点为重儿子，加粗的边是重边，其他没有加粗的是轻边
这棵树中的长度大于1的重链有两条：2—5和1—3—6—10
所有轻儿子可视作一个长度为1的重链

---

something about properties

• 若x是轻儿子，则有$x_{size}<=\frac{father(x{)}_{size}}{2}$

• 从根到某一点的路径上，不超过$lo{g}_{2}n$条重链，不超过$lo{g}_{2}n$条轻链

（不需要证明是因为我不会证）

---

预处理、维护和在线操作

其实和着概念一起看剩下三种东东，树剖还就真挺水的连模板都不用背
接下来的数据结构维护我们使用简单一点的线段树

---

预处理

首先用一个dfs遍历，求出每个点的$depth$、$father$、$size$以及重儿子$heavy$_$son$
其次再用一个dfs剖分，第二个$dfs$维护什么呢？

• 以优先走重边的原则，遍历出来一个dfs序
• $x_{top}$表示x位于的重链上的顶端节点编号
• $to$_$tree[x]$表示x在线段树中的位置
• 对于线段树中的第y个位置，$to$_$num[y]$为它对应的dfs序中的位置

剖分完以后，每一条重链相当于一个区间，我们维护处理完的数据结构即可

我们把上面那棵树剖分完以后线段树中的点顺序是这样的：
1，3，6，10，8，9，7，2，5，4 （加粗的点是在重链上的点）
在同一条重链上的点，在线段树的顺序中要连在一起（否则怎么维护呢）

剖树的时间复杂度$O(n)$

---

维护以及在线操作

change

因为已经搞过to_tree了，通过to_tree的标号在线段树中用单点修改即可
不要告诉我你不会单点修改
时间复杂度是线段树修改的$O({\log }_{2}n)$

---

query

询问$x$到$y$路径的极值（或者路径和等等），和求$LCA$一样边向上跳边记录答案
这里记录的答案通过查询数据结构得到
关于时间复杂度嘛……

---

关于时间复杂度？

对于我们这些蒟蒻来说最关键的还是时间复杂度的问题
用最普通的数据结构线段树来维护树链剖分的时间复杂度是$O(n+q{\log }_2^{2}n)$

后面那个$q{\log }_2^{2}n$什么东西？

由于求$LCA$是$O({\log }_{2}n)$的，统计答案的过程中还要查询数据结构又是$O({\log }_{2}n)$的时间
所以每个查询的时间复杂度就是$O({\log }_2^{2}n)$了

• 平常来说，对于树剖，时间应该是比树上倍增那个$O(n{\log }_{2}n)$的预处理优的

所以你看树剖还是非常有用的
还有用$LCT$维护可以做到$O(n{\log }_{2}n)$的时间还有LCT什么的你现在怎么可能会呢

---

重链剖分（在线）求LCA

树剖当然也能求LCA啦！并且比倍增还好打耶！
具体如下

• 若$x_{top}̸=y_{top}$，说明$x$和$y$不在同一条重链上
• 记$x$和$y$两点中top的深度较深的那个点为z
• 把$z$跳到$z_{to{p}_{father}}$
• 重复以上步骤，直到$x$和$y$在同一条重链上（即$x_{top}=y_{top}$）
• 此时$x$和$y$中$depth$小的点即为$LCA$

其实很好理解，跳到$z_{to{p}_{father}}$的原因是让z进入另一条重链免得程序卡住
而选择$top$浅的点而不是本身浅的点是防止跳到重链头超过$LCA$
不懂面壁去想，倍增你都听懂了，树剖的你听不懂就xxx了
那么时间复杂度$O({\log }_{2}n)$

---

code

• 当然求$LCA$没有各种权，不用打线段树啦！

#include
#define MAXN 30001

using namespace std;

int last[3*MAXN],next[3*MAXN],tov[3*MAXN];
int n,m,tot;

struct information
{
    int depth,father,size,heavy_son,top,to_tree,value;
}a[30001];

void insert(int x,int y)
{
    next[++tot]=last[x];
    last[x]=tot;
    tov[tot]=y;
}

void dfs1(int x,int father)
{
	int mx=-1;
	a[x].size=1;
	for (int i=last[x];i;i=next[i])
	{
		int j=tov[i];
		if (j!=father)
		{
			a[j].depth=a[x].depth+1;
			a[j].father=x;
			dfs1(j,x);
			a[x].size+=a[j].size;
			if (a[j].size>mx)
			{
				mx=a[j].size;
				a[x].heavy_son=j;
			}
		}
	}
}

void dfs2(int x,int father,int k)
{
	if (x==0)return;
	a[x].top=k;
	dfs2(a[x].heavy_son,x,k);
	for (int i=last[x];i;i=next[i])
	{
		int j=tov[i];
		if (j!=father && j!=a[x].heavy_son && j!=0)
		{
			dfs2(j,x,j);
		}
	}
}

int lca(int x,int y)
{
	while (a[x].top!=a[y].top)
	{
		if (a[a[x].top].depth>a[a[y].top].depth)
			x=a[a[x].top].father;
		else y=a[a[y].top].father;
	}
	return a[x].depth<a[y].depth?x:y;
}

int main()
{
	scanf("%d",&n);
	for (int i=1;i<n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		insert(x,y);
		insert(y,x);
	}
	a[1].depth=1;
	a[1].father=0;
	dfs1(1,0);
	dfs2(1,0,1);
	scanf("%d",&m);
	for (int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		printf("%d\n",lca(x,y));
	}
	return 0;
}

还是看例题吧

---

例题1：【JZO1738】Heatwave

problem

题目上面有所以就不重新贴了

---

analysis

我说过了倍增能做的题树剖都能做的嘛，所以树剖当然也能做这道题

其实在树剖里面这题算是模板题，而且树链剖分还看得很清楚
求完了$MST$后，我们还是照样把这棵$MST$剖分一下，用线段树维护区间最大值
这里我们求的是边权而不是点权，我们就把边权放到儿子节点上看成点权就可以了

求$LCA$时我们是一条重链一条重链地向上跳，这里我们是一样的——
每次跳一条重链的时候，用线段树维护好的区间最大值查询这条重链的点权最大值
（还有不要告诉我你不会线段树）

套上求$LCA$的意义也就是这样——

• 若$x_{top}̸=y_{top}$，记$x$和$y$两点中top的深度较深的那个点为z
• $temp=max(temp,tre{e}_{quer{y}_{max}}(1,1,n,a[a[z].top].t{o}_{tree},a[z].t{o}_{tree}))$
• 把$z$跳到$z_{to{p}_{father}}$

最后的$temp$即为答案，每个查询是$O({\log }_2^{2}n)$的时间复杂度

其实想一想，线段树是把每条重链当做区间来维护，意义十分显然
（注意一点就是求最大值时一定不要算上$LCA(x,y)$的值）

---

code

#include
#include
#define MAXN 15001
#define INF 1000000007

using namespace std;

int last[4*MAXN],next[4*MAXN],tov[4*MAXN],dis[4*MAXN];
int to_num[4*MAXN],father[MAXN];
int n,m,k,tot,total;

struct information
{
	int depth,father,size,heavy_son,top,to_tree,value;
}a[4*MAXN];

struct point
{
	int mx,ans;
}tree[4*MAXN];

struct dist
{
	int u,v,w;
}line[4*MAXN];

bool cmp(dist a,dist b)
{
	return a.w<b.w;
}

int getfather(int x)
{
	if (father[x]==0)return x;
	father[x]=getfather(father[x]);
	return father[x];
}

void insert(int x,int y,int z)
{
	next[++tot]=last[x];
	last[x]=tot;
	tov[tot]=y;
	dis[tot]=z;
}

void dfs1(int x,int father)
{
	int mx=-1;
	a[x].size=1;
	for (int i=last[x];i;i=next[i])
	{
		int j=tov[i];
		if (j!=father)
		{
			a[j].depth=a[x].depth+1;
			a[j].father=x;
			a[j].value=dis[i];
			dfs1(j,x);
			a[x].size+=a[j].size;
			if (a[j].size>mx)
			{
				mx=a[j].size;
				a[x].heavy_son=j;
			}
		}
	}
}

void dfs2(int x,int father,int top)
{
	if (x==0)return;
	a[x].top=top;
	a[x].to_tree=++total;
	to_num[total]=x;
	dfs2(a[x].heavy_son,x,top);
	for (int i=last[x];i;i=next[i])
	{
		int j=tov[i];
		if (j!=father && j!=a[x].heavy_son && j!=0)
		{
			dfs2(j,x,j);
		}
	}
}

void maketree(int t,int l,int r)
{
	if (l==r)
	{
		tree[t].mx=a[to_num[l]].value;
		return;
	}
	int mid=(l+r)/2;
	maketree(t*2,l,mid);
	maketree(t*2+1,mid+1,r);
	tree[t].mx=max(tree[t*2].mx,tree[t*2+1].mx);
}

int tree_query_max(int t,int l,int r,int x,int y)
{
	if (l==x && r==y)
	{
		return tree[t].mx;
	}
	int mid=(l+r)/2;
	if (y<=mid)
	{
		return tree_query_max(t*2,l,mid,x,y);
	}
	else if (x>mid)
	{
		return tree_query_max(t*2+1,mid+1,r,x,y);
	}
	else return max(tree_query_max(t*2,l,mid,x,mid),tree_query_max(t*2+1,mid+1,r,mid+1,y));
}

int query_max(int x,int y)
{
	int temp=-1;
	while (a[x].top!=a[y].top)
	{
		if (a[a[x].top].depth>a[a[y].top].depth)
		{
			temp=max(temp,tree_query_max(1,1,n,a[a[x].top].to_tree,a[x].to_tree));
			x=a[a[x].top].father;
		}
		else
		{
			temp=max(temp,tree_query_max(1,1,n,a[a[y].top].to_tree,a[y].to_tree));
			y=a[a[y].top].father;
		}
	}
	if (x==y)return temp;
	if (a[x].depth<a[y].depth)
	{
		temp=max(temp,tree_query_max(1,1,n,a[a[x].heavy_son].to_tree,a[y].to_tree));
	}
	else
	{
		temp=max(temp,tree_query_max(1,1,n,a[a[y].heavy_son].to_tree,a[x].to_tree));
	}
	return temp;
}

int main()
{
	//freopen("readin.txt","r",stdin);
	scanf("%d%d%d",&n,&m,&k);
	for (int i=1;i<=m;i++)
	{
		scanf("%d%d%d",&line[i].u,&line[i].v,&line[i].w);
	}
	sort(line+1,line+m+1,cmp);
	for (int i=1;i<=m;i++)
	{
		if (getfather(line[i].u)!=getfather(line[i].v))
		{
			father[getfather(line[i].u)]=getfather(line[i].v);
			insert(line[i].u,line[i].v,line[i].w);
			insert(line[i].v,line[i].u,line[i].w);
		}
	}
	a[1].depth=1;
	dfs1(1,0),dfs2(1,0,1);
	maketree(1,1,n);
	for (int i=1;i<=k;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		printf("%d\n",query_max(x,y));
	}
	return 0;
}

一定读懂这段代码再看下面的题
否则会爽炸天

---

例题2：【JZO3534】【luoguP1967】货车运输

problem

Description

A 国有 n 座城市，编号从 1 到 n，城市之间有 m 条双向道路。每一条道路对车辆都有重量限制，简称限重。现在有 q
辆货车在运输货物，司机们想知道每辆车在不超过车辆限重的情况下，最多能运多重的货物。

Input

第一行有两个用一个空格隔开的整数 n，m，表示 A 国有 n 座城市和 m 条道路。

接下来 m 行每行 3 个整数 x、y、z，每两个整数之间用一个空格隔开，表示从 x 号城市到 y 号城市有一条限重为 z 的道路。注意：x
不等于 y，两座城市之间可能有多条道路。

接下来一行有一个整数 q，表示有 q 辆货车需要运货。

接下来 q 行，每行两个整数 x、y，之间用一个空格隔开，表示一辆货车需要从 x 城市运输货物到 y 城市，注意：x 不等于 y。

Output

输出共有 q 行，每行一个整数，表示对于每一辆货车，它的最大载重是多少。如果货车不能到达目的地，输出-1。

Sample Input

4 3

1 2 4

2 3 3

3 1 1

3

1 3

1 4

1 3

Sample Output

3

-1

3

Data Constraint

对于 30%的数据，0 < n < 1,000，0 < m < 10,000，0 < q < 1,000；

对于 60%的数据，0 < n < 1,000，0 < m < 50,000，0 < q < 1,000；

对于 100%的数据，0 < n < 10,000，0 < m < 50,000，0 < q < 30,000，0 ≤ z ≤
100,000。

---

analysis

又一个套路$MST$配树链剖分就是不想上倍增

和上面heatwave不同的是，这里的原图不一定连通，且两城之间有多条边

• 虽说不一定连通，还是直接上一次最大生成树即可

• 多条边就把多条边中最大权值的边留下，其他的边不必管

剩下线段树维护点权最小值即和heatwave的一模一样

但必须注意一点：判断联通性的问题
我们不能只从$1$节点开始剖一次树，而是必须从所有未访问到的节点开始剖树

至于判断联通性，一开始我去做洛谷的时候，是在求$LCA$途中判断是否连通，但是WA了
其实除了$kruskal$用的一次并查集外，我们可以再用一次并查集，把$MST$上的边再搞一次
需要访问$x,y$城市时只需询问$getfather(x)=getfather(y)?$即可

---

code

#include
#define MAXN 10001
#define MAXM 50001

using namespace std;

int last[2*MAXM],next[2*MAXM],tov[2*MAXM],dis[2*MAXM];
bool visited[MAXN],flag[MAXM]; 
int to_num[MAXN],father[MAXN],tree[4*MAXN];
int n,m,q,tot,total;

struct array
{
	int x,y,z;
}dist[2*MAXM];

struct information
{
    int depth,father,size,heavy_son,top,to_tree,value;
}a[MAXN];

bool cmp(array a,array b)
{
	return a.z>b.z;
}

int min(int x,int y)
{
	return x<y?x:y;
}

int getfather(int x)
{
	if (father[x]==0)return x;
	return father[x]=getfather(father[x]);
}

void insert(int x,int y,int z)
{
	next[++tot]=last[x];
	last[x]=tot;
	tov[tot]=y;
	dis[tot]=z;
}

void dfs1(int x,int father)
{
	visited[x]=0;
	a[x].size=1;
	int mx=-1;
	for (int i=last[x];i;i=next[i])
	{
		int j=tov[i];
		if (j!=father)
		{
			if (visited[j]==0)
			{
				a[j].value+=dis[i];
				continue;
			}
			a[j].depth=a[x].depth+1;
			a[j].value=dis[i];
			a[j].father=x;
			dfs1(j,x);
			a[x].size+=a[j].size;
			if (a[j].size>mx)
			{
				a[x].heavy_son=j;
				mx=a[j].size;	
			} 
		}
	}
}

void dfs2(int x,int top)
{
	if (x==0)return;
	a[x].top=top;
	a[x].to_tree=++total;
	to_num[total]=x;
	dfs2(a[x].heavy_son,top);
	for (int i=last[x];i;i=next[i])
	{
		int j=tov[i];
		if (j!=a[x].father && j!=a[x].heavy_son && j!=0)
		{
			dfs2(j,j);
		}
	}
}

void maketree(int t,int l,int r)
{
	if (l==r)
	{
		tree[t]=a[to_num[l]].value;
		return;
	}
	int mid=(l+r)/2;
	maketree(2*t,l,mid),maketree(2*t+1,mid+1,r);
	tree[t]=min(tree[2*t],tree[2*t+1]);
}

bool judge(int x,int y)
{
	while (a[x].top!=a[y].top)
	{
		if ((x==a[x].top && a[x].father==0)||(y==a[y].top && a[y].father==0))return 0;
		if (a[a[x].top].depth>a[a[y].top].depth)
		{
			x=a[a[x].top].father;
		}
		else
		{
			y=a[a[y].top].father;
		}
	}
	return 1;
}

int tree_query_min(int t,int l,int r,int x,int y)
{
	if (l==x && y==r)
	{
		return tree[t];
	}
	int mid=(l+r)/2;
	if (y<=mid)
	{
		return tree_query_min(t*2,l,mid,x,y);
	}
	else if (x>mid)
	{
		return tree_query_min(t*2+1,mid+1,r,x,y);
	}
	else
	{
		return min(tree_query_min(t*2,l,mid,x,mid),tree_query_min(t*2+1,mid+1,r,mid+1,y));
	}
}

int query_min(int x,int y)
{
	int temp=1000000007;
	while (a[x].top!=a[y].top)
	{
		if (a[a[x].top].depth>a[a[y].top].depth)
		{
			temp=min(temp,tree_query_min(1,1,n,a[a[x].top].to_tree,a[x].to_tree));
			x=a[a[x].top].father;	
		}
		else
		{
			temp=min(temp,tree_query_min(1,1,n,a[a[y].top].to_tree,a[y].to_tree));
			y=a[a[y].top].father;
		}
	} 
	if (x==y)return temp;
	if (a[x].depth<a[y].depth)
	{
		return min(temp,tree_query_min(1,1,n,a[a[x].heavy_son].to_tree,a[y].to_tree));
	}
	else
	{
		return min(temp,tree_query_min(1,1,n,a[a[y].heavy_son].to_tree,a[x].to_tree));
	}
}

int main()
{
	//freopen("read.txt","r",stdin);
	scanf("%d%d",&n,&m);
	for (int i=1;i<=m;i++)
	{
		scanf("%d%d%d",&dist[i].x,&dist[i].y,&dist[i].z);
	}
	sort(dist+1,dist+m+1,cmp);
	for (int i=1;i<=m;i++)
	{
		int u=dist[i].x,v=dist[i].y,w=dist[i].z;
		if (getfather(u)!=getfather(v))
		{
			father[getfather(u)]=v;
			insert(u,v,w),insert(v,u,w);
			flag[i]=1;
		}
	}
	memset(visited,1,sizeof(visited));
	for (int i=1;i<=n;i++)
	if (visited[i])
	{
		a[i].depth=1;
		a[i].father=0;
		dfs1(i,0),dfs2(i,i);
	}
	maketree(1,1,n);
	memset(father,0,sizeof(father));
	for (int i=1;i<=m;i++)
	if (flag[i])
	{
		int u=dist[i].x,v=dist[i].y;
		father[getfather(u)]=getfather(v);
	}
	scanf("%d",&q);
	while (q--)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		if (getfather(x)==getfather(y))
		{
			printf("%d\n",query_min(x,y));
		}
		else printf("-1\n");
	}
	return 0;
}

---

例题3：【JZOJ2256】【ZJOI2008】树的统计

problem

Description

一棵树上有n个节点，编号分别为1到n，每个节点都有一个权值w。 　　我们将以下面的形式来要求你对这棵树完成一些操作：
　　I. CHANGE u t : 把结点u的权值改为t 　　II. QMAX u v: 询问从点u到点v的路径上的节点的最大权值
　　III. QSUM u v: 询问从点u到点v的路径上的节点的权值和 　　注意：从点u到点v的路径上的节点包括u和v本身

Input

输入文件的第一行为一个整数n，表示节点的个数。 　　接下来n – 1行，每行2个整数a和b，表示节点a和节点b之间有一条边相连。
　　接下来n行，每行一个整数，第i行的整数wi表示节点i的权值。 　　接下来1行，为一个整数q，表示操作的总数。
　　接下来q行，每行一个操作，以“CHANGE u t”或者“QMAX u v”或者“QSUM u v”的形式给出。

Output

对于每个“QMAX”或者“QSUM”的操作，每行输出一个整数表示要求输出的结果。

Sample Input
QMAX 3 4
QMAX 3 3
QMAX 3 2
QMAX 2 3
QSUM 3 4
QSUM 2 1
CHANGE 1 5
QMAX 3 4
CHANGE 3 6
QMAX 3 4
QMAX 2 4
QSUM 3 4

Sample Output

4 1 2 2 10 6 5 6 5 16

Data Constraint

Hint

【数据说明】
　　对于100％的数据，保证1<=n<=30000，0<=q<=200000；中途操作中保证每个节点的权值w在-30000到30000之间。

---

analysis

这题还是树剖经典例题
看懂$heatwave$的树剖做法，这题就比较简单啦

这里的线段树要维护和查询两个值了，是区间最大值和区间和
还是一样地，求$LCA$的同时用线段树查询整条重链的区间最大值和区间和
我懒得再讲两种查询了

至于$change$操作，由于我们已经把每个点在线段树中的编号（to_tree）处理出来了
所以我们直接用线段树的单点修改就可以在线段树里面直接修改指定节点
修改完以后，推回父亲节点，更新线段树即可，change成功解决
$change$的时间复杂度$O({\log }_{2}n)$

---

code

树剖打250行，醉了

#include
#define MAXN 30001
#define INF 1000000007

using namespace std;

int last[3*MAXN],next[3*MAXN],tov[3*MAXN];
int to_num[MAXN];
int n,m,tot,total;
char st[10];

struct information
{
    int depth,father,size,heavy_son,top,to_tree,value;
}a[MAXN];

struct point
{
	int mx,ans;
}tree[MAXN*4];

int max(int x,int y)
{
	return x>y?x:y;
}

void insert(int x,int y)
{
    next[++tot]=last[x];
    last[x]=tot;
    tov[tot]=y;
}

void dfs1(int x,int father)
{
    int mx=-1;
    a[x].size=1;
    for (int i=last[x];i;i=next[i])
    {
        int j=tov[i];
        if (j!=father)
        {
            a[j].depth=a[x].depth+1;
            a[j].father=x;
            dfs1(j,x);
            a[x].size+=a[j].size;
            if (a[j].size>mx)
            {
                mx=a[j].size;
                a[x].heavy_son=j;
            }
        }
    }
}

void dfs2(int x,int father,int k)
{
    if (x==0)return;
    a[x].top=k;
    a[x].to_tree=++total;
    to_num[total]=x;
    dfs2(a[x].heavy_son,x,k);
    for (int i=last[x];i;i=next[i])
    {
        int j=tov[i];
        if (j!=father && j!=a[x].heavy_son && j!=0)
        {
            dfs2(j,x,j);
        }
    }
}

void maketree(int t,int l,int r)
{
	if (l==r)
	{
		tree[t].ans=tree[t].mx=a[to_num[l]].value;
		return;
	}
	int mid=(l+r)/2;
	maketree(t*2,l,mid);
	maketree(t*2+1,mid+1,r);
	tree[t].ans=tree[t*2].ans+tree[t*2+1].ans;
	tree[t].mx=max(tree[t*2].mx,tree[t*2+1].mx);
}

void change(int t,int l,int r,int x,int y)
{
	if (l==r)
	{
		tree[t].ans=tree[t].mx=y;
		return;
	}
	int mid=(l+r)/2;
	if (x<=mid)
	{
		change(t*2,l,mid,x,y);
	}
	else
	{
		change(t*2+1,mid+1,r,x,y);
	}
	tree[t].mx=max(tree[t*2].mx,tree[t*2+1].mx);
	tree[t].ans=tree[t*2].ans+tree[t*2+1].ans;
}

int tree_query_max(int t,int l,int r,int x,int y)
{
    if (l==x && r==y)
    {
        return tree[t].mx;
    }
    int mid=(l+r)/2;
    if (y<=mid)
    {
        return tree_query_max(t*2,l,mid,x,y);
    }
    else if (x>mid)
    {
        return tree_query_max(t*2+1,mid+1,r,x,y);
    }
    else
    {
        return max(tree_query_max(t*2,l,mid,x,mid),tree_query_max(t*2+1,mid+1,r,mid+1,y));
    }
}

int tree_query_sum(int t,int l,int r,int x,int y)
{
    if (l==x && r==y)
    {
        return tree[t].ans;
	}
    int mid=(l+r)/2;
    if (y<=mid)
	{
        return tree_query_sum(t*2,l,mid,x,y);
    }
    else if (x>mid)
	{
        return tree_query_sum(t*2+1,mid+1,r,x,y);
    }
    else
    {
        return tree_query_sum(t*2,l,mid,x,mid)+tree_query_sum(t*2+1,mid+1,r,mid+1,y);
    }
}

int query_max(int x,int y)
{
	int temp=-INF;
    while (a[x].top!=a[y].top)
    {
        if (a[a[x].top].depth>a[a[y].top].depth)
		{
			temp=max(temp,tree_query_max(1,1,n,a[a[x].top].to_tree,a[x].to_tree));
			x=a[a[x].top].father;
		}
        else 
		{
			temp=max(temp,tree_query_max(1,1,n,a[a[y].top].to_tree,a[y].to_tree));
			y=a[a[y].top].father;
		}
    }
	if (a[x].depth<a[y].depth)
	{
        temp=max(temp,tree_query_max(1,1,n,a[x].to_tree,a[y].to_tree));
    }
    else
    {
	 	temp=max(temp,tree_query_max(1,1,n,a[y].to_tree,a[x].to_tree));
	}
    return temp;
}

int query_sum(int x,int y)
{
	int temp=0;
    while (a[x].top!=a[y].top)
	{
        if (a[a[x].top].depth>a[a[y].top].depth)
		{
			temp+=tree_query_sum(1,1,n,a[a[x].top].to_tree,a[x].to_tree);
			x=a[a[x].top].father;
		}
        else 
		{
			temp+=tree_query_sum(1,1,n,a[a[y].top].to_tree,a[y].to_tree);
			y=a[a[y].top].father;
		}
    }
	if (a[x].depth<a[y].depth)
	{
        temp+=tree_query_sum(1,1,n,a[x].to_tree,a[y].to_tree);
    }
    else
    {
	 	temp+=tree_query_sum(1,1,n,a[y].to_tree,a[x].to_tree);
	}
    return temp;
}

int main()
{
	//freopen("readin.txt","r",stdin);
	
    scanf("%d",&n);
    for (int i=1;i<n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        insert(x,y);
        insert(y,x);
    }
    for (int i=1;i<=n;i++)
    {
    	scanf("%d",&a[i].value);
	}
    a[1].depth=1,a[1].father=0;
    dfs1(1,0),dfs2(1,0,1);
    maketree(1,1,n);
    scanf("%d",&m);
    for (int i=1;i<=m;i++)
    {
    	int x,y;
    	scanf("%s %d %d",&st,&x,&y);
    	if (st[1]=='M')
    	{
    		printf("%d\n",query_max(x,y));
		}
		else if (st[1]=='S')
		{
			printf("%d\n",query_sum(x,y));
		}
		else
		{	
			change(1,1,n,a[x].to_tree,y);
		}
	}    
    return 0;
}

---

例题4：【JZOJ1175】【BZOJ2238】【IOI2008】生成树

problem

Description

给出一个N个点M条边的无向带权图，以及Q个询问，每次询问在图中删掉一条边后图的最小生成树。(各询问间独立，每次询问不对之后的询问产生影响，即被删掉的边在下一条询问中依然存在)

Input

第一行两个正整数N,M(N<=50000,M<=100000)表示原图的顶点数和边数。
下面M行，每行三个整数X,Y,W描述了图的一条边(X,Y)，其边权为W（W<=10000）。保证两点之间至多只有一条边。
接着一行一个正整数Q，表示询问数。(1<=Q<=100000)
下面Q行，每行一个询问，询问中包含一个正整数T，表示把编号为T的边删掉(边从1到M按输入顺序编号)。

Output

Q行，对于每个询问输出对应最小生成树的边权和的值，如果图不连通则输出“Not connected”

Sample Input

4 4 1 2 3 1 3 5 2 3 9 2 4 1 4 1 2 3 4

Sample Output

15 13 9 Not connected

Data Constraint

Hint

数据规模： 10%的数据N,M,Q<=100。 另外30%的数据，N<=1000 100%的数据如题目。

---

analysis

• 还有第四道例题（不要看到“IOI”什么的就不敢做了）

正解还是——MST+树链剖分
奇怪的是静态树上问题MST+树剖是不是万能的…？

想一想即知，如果删去的边不在原图的$MST$上，对原答案没有影响
但是如果删去了$MST$上的边，那么其他的$MST$树边一定不变
那此时要找的只是一条非$MST$上的边，且要求最短，显然是在树链上

我们在求完$MST$后，用树链剖分维护每条非MST树边能够使多少条MST树边删去后连通
说着很拗口，但操作还是很$simple$的，标记永久化一下即可
当然原图就是不连通的话，$q$个操作全都输出**“Not connected”**
时间复杂度为$O(n{\log }_2^{2}n)$

---

code

#include
#define MAXN 50001
#define MAXM 100001 

using namespace std;

int last[2*MAXM],next[2*MAXM],tov[2*MAXM],dis[2*MAXM];
int father[MAXN],where[MAXM],to_num[MAXN],tree[4*MAXN],ref[2*MAXN];
int n,m,q,tot,total,ans;

int min(int x,int y)
{
    return x<y?x:y;
}

int read()
{
    int x=0,f=1;
    char ch=getchar();
    while (ch<'0' || '9'<ch)
    {
        if (ch=='-')f=-1;
        ch=getchar();   
    }
    while ('0'<=ch && ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}

struct information
{
    int depth,father,size,heavy_son,top,to_tree,value;
}a[MAXN];

struct dist
{
    int x,y,z,num;
    bool flag;
}line[MAXM];

bool cmp(dist a,dist b)
{
    return a.z<b.z; 
}

bool cmp1(dist a,dist b)
{
    return a.num<b.num;
}

int getfather(int x)
{
    return !father[x]?x:father[x]=getfather(father[x]);
}

void insert(int x,int y,int z)
{
    next[++tot]=last[x];
    last[x]=tot;
    tov[tot]=y;
    dis[tot]=z;
}

void dfs1(int x,int father)
{
    a[x].size=1;
    int mx=-1;
    for (int i=last[x];i;i=next[i])
    {
        int j=tov[i];
        if (j!=father && j!=0)
        {
            a[j].depth=a[x].depth+1;
            a[j].father=x;
            ref[dis[i]]=j;
            dfs1(j,x);
            a[x].size+=a[j].size;
            if (a[j].size>mx)
            {
                mx=a[j].size;
                a[x].heavy_son=j;
            }
        }
    }
}

void dfs2(int x,int top)
{
    if (x==0)return;
    a[x].top=top;
    a[x].to_tree=++total;
    to_num[total]=x; 
    dfs2(a[x].heavy_son,top);
    for (int i=last[x];i;i=next[i])
    {
        int j=tov[i];
        if (j!=a[x].father && j!=a[x].heavy_son && j!=0)
        {
            dfs2(j,j);
        }
    }
}

void change(int t,int l,int r,int x,int y,int z)
{
    if (l==x && y==r)
    {
        tree[t]=min(tree[t],z);
        return;
    }
    int mid=(l+r)/2;
    if (y<=mid)
    {
        change(t*2,l,mid,x,y,z);
    }
    else if (x>mid)
    {
        change(t*2+1,mid+1,r,x,y,z);
    }
    else
    {
        change(t*2,l,mid,x,mid,z);
        change(t*2+1,mid+1,r,mid+1,y,z);
    }
    //tree[t]=min(tree[t*2],tree[t*2+1]);
}

int query(int t,int l,int r,int x)
{
    if (l==r)
    {
        return tree[t];
    }
    int mid=(l+r)/2;
    if (x<=mid)return min(tree[t],query(t*2,l,mid,x));
    else return min(tree[t],query(t*2+1,mid+1,r,x));
}

void modify(int x,int y,int z)
{
    while (a[x].top!=a[y].top)
    {
        if (a[a[x].top].depth>a[a[y].top].depth)
        {
            change(1,1,n,a[a[x].top].to_tree,a[x].to_tree,z);
            x=a[a[x].top].father;
        }
        else
        {
            change(1,1,n,a[a[y].top].to_tree,a[y].to_tree,z);
            y=a[a[y].top].father;
        }
    }
    if (x==y)return;
    if (a[x].depth>a[y].depth)
    {
        change(1,1,n,a[a[y].heavy_son].to_tree,a[x].to_tree,z);
    }
    else
    {
        change(1,1,n,a[a[x].heavy_son].to_tree,a[y].to_tree,z);
    }
}

int main()
{
    //freopen("read.txt","r",stdin);
    n=read(),m=read(); 
    for (int i=1;i<=m;i++)
    {
        line[i].x=read(),line[i].y=read(),line[i].z=read();
        line[i].num=i;  
    }
    if (m<n-1)
    {
        q=read();
        while (q--)printf("Not connected\n");
        return 0;
    }
    sort(line+1,line+m+1,cmp);
    for (int i=1;i<=m;i++)
    {
        int u=line[i].x,v=line[i].y,w=line[i].z;
        if (getfather(u)!=getfather(v))
        {
            father[getfather(u)]=v;
            line[i].flag=1;
            ans+=w;
            insert(u,v,line[i].num);
            insert(v,u,line[i].num);
        }
    }
    a[1].depth=1;
    a[1].father=0;
    dfs1(1,0),dfs2(1,1);
    memset(tree,0x3f,sizeof(tree));
    sort(line+1,line+m+1,cmp1);
    for (int i=1;i<=m;i++)
    {
        if (!line[i].flag)
        {
            modify(line[i].x,line[i].y,line[i].z);
        }
    } 
    q=read();
    while (q--)
    {
        int x=read();
        if (!line[x].flag)
        {
            printf("%d\n",ans);
        }
        else
        {
            int xx=query(1,1,n,a[ref[x]].to_tree);
            if(xx==0x3f3f3f3f)
            {
                printf("Not connected\n");
            }
            else 
            {
                printf("%d\n",ans-line[x].z+xx); 
            }
        } 
    }
    return 0;
}

---

长链剖分

• 待填坑

---

树剖大法好

最近做模拟赛，看到树上问题就开码树剖 （我变成无脑xxxx玄手了么）
但是树剖对付静态树问题基本都能完美解决
树剖用处确实非常非常多，不仅要熟练运用，还要做到触类旁通、用老知识解决新题目
我不是树剖讲师所以树剖学的还是不好

动态树问题呢？树剖GG，祭出$LCT$吧
（LCT明明比树剖高级多了）

---

LCT（Link-Cut Tree）

---

玄♂妙的动态树问题

静态树问题在前面已经见识过了
就是树的形态不发生变化，只是树上的权值变化，用数据结构随便维护一下的问题罢了

但是树的形态如果会变化呢？（例如添、删树边操作等）
这就是 动态树问题（Dynamic Tree Problem） 了

---

然而Link-Cut Tree并不能吃

杨哲的《QTREE 解法的一些研究》 你应该听说过
由于百度像csdn一样要XX币才能下载那些文档，就百度云共享一波啦
这里下载，uuq0

LCT（Link-Cut Tree），解决动态树问题的一种算法
LCT≈splay+树剖，是解决动态树问题的一把利器
核心思想就是借鉴树剖的 轻重边 等概念，用比线段树灵活的$splay$来维护一棵树（森林）
意会就好
（但真相是tarjan老爷子是在发明LCT之后才发明的splay）

---

the most advantages

动态树问题通常要求你对一棵树进行切割和拼接等操作，然后再在上面维护传统数据结构可维护的值
树剖做不了的软肋在于重儿子和重链早就剖分（预处理）好了
怎么添、删边？暴力重构所有重儿子和整个线段树？

100%GG

不用$LCT$也能勉强做某些动态树问题了 （注意某些）
如果只有添边或只有删边且不要求强制在线的题目，用离线+树剖+splay/动态开点线段树是可以做的
虽说树剖勉强支持删边操作，但这毕竟不是最通用、最完美的做法
什么东西能真正完美地解决这一类动态树问题呢？

Link-Cut Tree算法

而且$LCT$能做的除了动态树问题还有

• 任何树剖题

• 可支持删边的并查集

• 可做不用排序的$kruskal$（动态加边的$MST$并查集）

• 等……

我之前不是说过树上倍增能做的题树剖一定能做吗
而树链剖分能做的题$LCT$也一定能做

LCA呢？
LCT是不可以求动态树上的LCA的……

为什么不能求？这个等下再说吧

---

LCT之模样与概念

看看样子先

这就是一个LCT

$LCT$维护的其实算是一个连通性森林

---

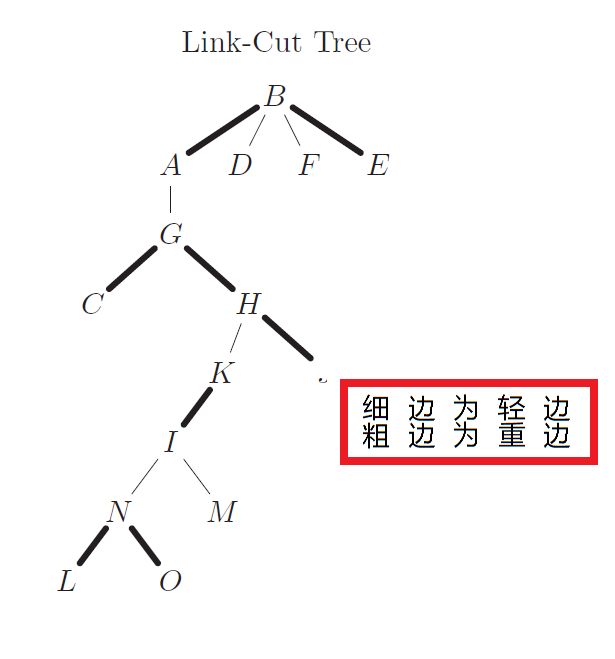
一些概念

• Preferred Child：重儿子，重儿子与父亲节点在同一棵splay中，一个节点至多一个重儿子
• Preferred Edge：重边，连接父亲节点和重儿子的边
• Preferred Path ：重链，由重边及重边连接的节点构成的链

你看这个明显和树剖的东东一个鬼样所以可以略过
原来的那些名称都叫什么“偏好”XX的，感觉用树剖名词就可以了

接下来是$LCT$里一个独♂特的东西

• Auxiliary Tree：辅助树

• 由一条重链上的所有节点所构成的Splay称作这条链的辅助树

• 每个点的键值为这个点的深度，即这棵Splay的中序遍历是这条链从链顶到链底的所有节点构成的序列

• 辅助树的根节点的父亲指向链顶的父亲节点，然而链顶的父亲节点的儿子并不指向辅助树的根节点
• （也就是说父亲不认轻儿子只认重儿子，儿子都认父亲）
• 这条性质为后来的操作提供了依据

上面框框里面是上网copy的，不知道怎么解释
必须注意辅助树（splay）的根≠原树的根

• 首先不要把LCT 真的当成一棵树

LCT不是树！！！是个森林OK？LCA都求不了这叫做树么？
在同一棵splay里面当然可以暴力求LCA，但这有意义么？

• 其次，为什么LCT里的点不认轻重儿子？
  在一个splay里的点不就是父亲和重儿子和重儿子的重儿子……么？

• 对上面的定义简单点说，在同一条“重链”里的所有点在一个splay中
  不懂就看上面那个$LCT$自己理解，如$B$与$A$和$E$是在一个splay里的
  这个明明很简单

• splay过程中，树的形态可以变化如

但是原树是不会变的

• LCT还有个特点，就是不用记录节点编号
  因为一个点的右儿子的深度是比它的大的，不像splay一样需要查找什么的：D

• 其实更值得一提的是上面提到的虚边（也就是对应树剖的轻边）的那个东西
  虚边$pf$储存在一个splay的根节点，$pf[x]$为$x$在LCT里的父亲（即在不在当前辅助树里的那个）
  而$fa[x]$则是splay中$x$的父亲，不要把这个搞混
  例子：图中$pf[G]=A$而$fa[G]=0$，$pf[D]=0$而$fa[D]=B$
  同样自己去看图理解懒得多说

可以这样想：两个重链是用一条虚边连接的，没有虚边不就成一条重链了么？

看完这些，其实LCT还是很简单的……

那么，不看懂概念怎么可以去学LCT的操作呢？

---

LCT之核心操作

请务必认认真真地阅读以下内容否则LCT你就学不会了
一句话说了N遍

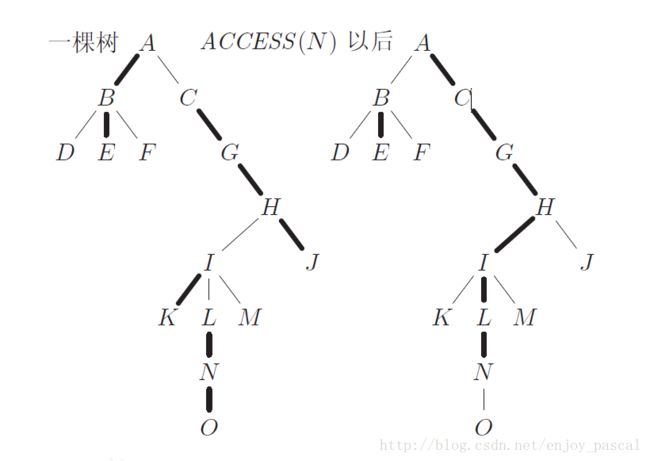
operation 1：access

access操作是LCT里最基础、最重要的操作

定义$access(x)$操作就是把$x$的重儿子与$x$断开，然后把从整个LCT的根到$x$之间的路径都变为重边

access操作其实是很简单的

• 若现在要$access$节点$x$，每一次把$x$旋转到当前辅助树的根

• 此时$x$的右儿子深度比$x$大，即右儿子是重儿子，我们自然而然的就要把它给删掉

• 把$x$连上$pf[x]$所在的辅助树 （splay） 里，然后$pf[t[x][1]]=x,fa[t[x][1]]=0$

• 简单点说就是把$x$的右儿子作为辅助树的新根，并连一条向$x$的虚边

• 重复以上操作，直到$pf[x]=fa[x]=0$

这个不简单吗？

---

时间复杂度呢？

• tarjan老爷子说，$splay$一次的时间复杂度是$O({\log }_{2}n)$

• 整个$access$要进行几次旋转操作呢？

• 把若干个小辅助树合并为一个大辅助树，只进行一次$splay$操作

• 由于$splay$均摊$O({\log }_{2}n)$，又因为每次只对一个大的辅助树$splay$，我们可以大胆想象得出只有$O({\log }_{2}n)$的时间

• 所以$access$操作的均摊时间是$O({\log }_{2}n)$

以后任何对access操作时间复杂度有疑问的请去找tarjan老爷子喝茶
问我没用

---

code

cc人生赢家的LCT好漂亮啊

void down(int x) 
{
    if (a[x].rev) 
    {
        reverse(t[x][0]),reverse(t[x][1]);
        a[x].rev=0;
    }
}

void update(int x) 
{
	if(x)
	{
		a[x].size=a[t[x][0]].size+a[t[x][1]].size+1;
	} 
}

void downdata(int x) 
{
    while (x)st[++st[0]]=x,x=fa[x];	
    while (st[0])down(st[st[0]--]);
}
//从x到辅助树的根的整条路径上的边都要下传翻转标记
//……其实也就是暴力下传标记
int lr(int x) 
{
	return t[fa[x]][1]==x;
}
	
void rotate(int x) 
{
    int y=fa[x],k=lr(x);
    t[y][k]=t[x][!k]; 
	if(t[x][!k])fa[t[x][!k]]=y;
    fa[x]=fa[y];
	if(fa[y])t[fa[y]][lr(y)]=x;    
    t[x][!k]=y; 
	fa[y]=x; 
	pf[x]=pf[y];
    update(y),update(x);
}

void splay(int x,int y) 
{
    //downdata(x);
    while(fa[x]!=y)
	{
        if(fa[fa[x]]!=y)
        {
            if(lr(x)==lr(fa[x]))rotate(fa[x]); 
			else rotate(x);
        } 
        rotate(x);
    }
}

void access(int x) 
{
    for (int y=0;x;update(x),y=x,x=pf[x])
    {
        splay(x,0);
		fa[t[x][1]]=0;
		pf[t[x][1]]=x;
        t[x][1]=y;
		fa[y]=x;
		pf[y]=0;
    }
}

---

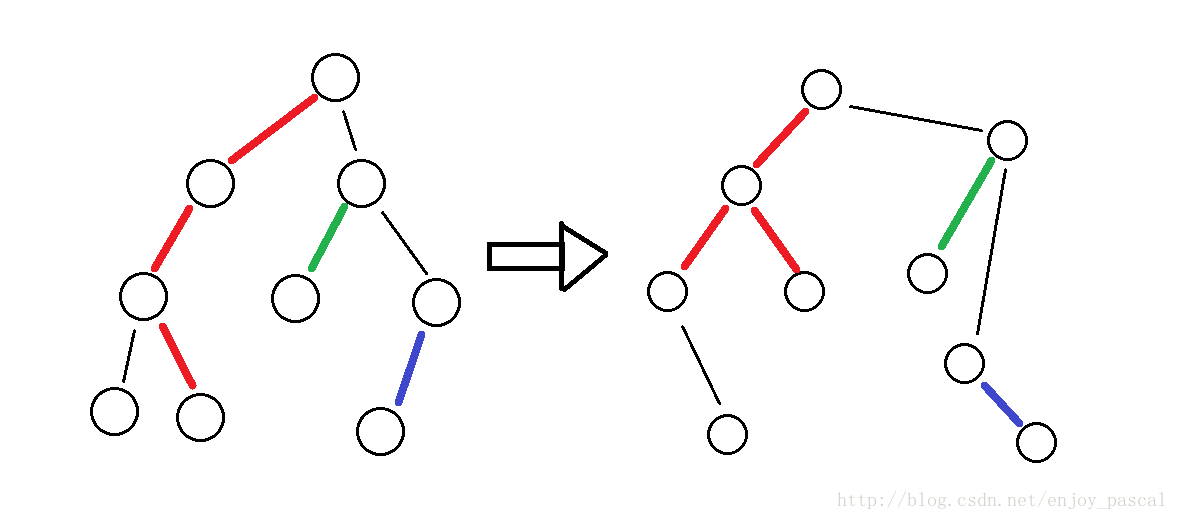
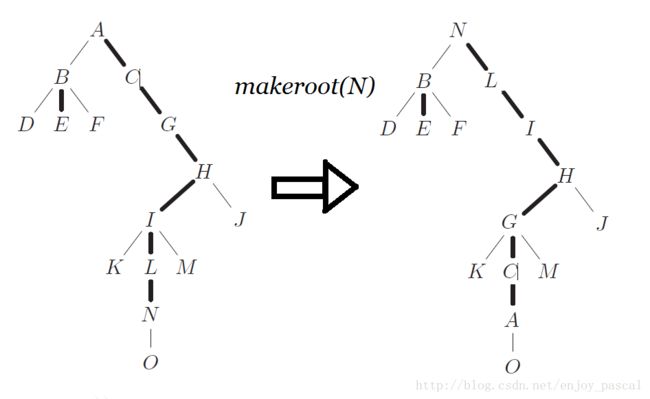
operation 2：makeroot

makeroot操作和access操作是LCT的最核心的操作
其他操作视题而定，但makeroot和access必不可少

定义$makeroot(x)$操作就是将$x$所在的splay翻转，使$x$变为原LCT树的根

大概这样吧……
不算$access$的话$makeroot$只有splay一次的时间复杂度为$O(lo{g}_{2}n)$

makeroot不就更简单了？

• 首先$access(x)$后，此时的$x$是辅助树中深度最大的点，接着把$x$旋转（splay）到LCT的根

• 而此时在辅助树中，除了$x$的其他点都是其父亲的左儿子

• 然后再splay区间翻转即可，打上lazy-tag标记

• 然后$makeroot$才成功解决，如上图的那种样子

---

code

void swap(int &x,int &y)
{
	int z=x;
	x=y;
	y=z;
}

void reverse(int x) 
{
	if(x)
	{
		a[x].rev^=1;
		swap(t[x][0],t[x][1]);
	}
}

void down(int x) 
{
	if (a[x].rev) 
	{
		reverse(t[x][0]),reverse(t[x][1]);
		a[x].rev=0;
	}
}

void makeroot(int x) 
{
    access(x); 
	splay(x,0); 
	reverse(x);
}

---

operation 3：link

link和cut嘛……所以LCT要叫Link-Cut Tree啊

定义$link(x,y)$操作就是将节点$x$连到节点$y$的儿子
link太简单了不想放图

link操作就太简单了

• $makeroot(x)$后，此时$x$是原LCT的根

• 此时$x$没有$fa$，而从$y$连向$x$会冲掉原来$y$的$fa$

• 所以从$x$向$y$连一条虚边，即$pf[x]=y$

---

code

void link(int x,int y) 
{
    makeroot(x); 
	pf[x]=y;
}

---

operation 4：cut

定义$cut(x,y)$操作就是将节点$x$（x是y的儿子）与父亲$y$断开
cut太简单了也不想放图

cut和link其实很类似

• $makeroot(x)$且$access(y)$后，$x$是原树的根，且$x$和$y$在同一splay里

• 然后$splay(x,0)$，保证$x$是根，又由于$x,y$连通，所以此时$y$是$x$的右儿子

• 所以$tree[x][1]=pf[y]=fa[y]=0$就好了

---

code

void cut(int x,int y) 
{
    makeroot(x); 
    access(y);
    splay(x,0);
    t[x][1]=fa[y]=pf[y]=0;
    update(x);
}

---

operation 5：getroot

定义$getroot(x)$为$x$节点当前辅助树的根
退化版并查集路径压缩

$getroot$小学生级别难度

• 暴力把$x$向上跳，直到$fa[x]=0$

• 没了

---

code

int getroot(int x)
{
    while (fa[x])x=fa[x];
    return x;
}

---

operation 6：judge

定义$judge(x,y)$，若$x,y$联通则为$True$，否则为$False$
退化版并查集集合查询

比$getroot$稍微难一丁点

• $makeroot(x),access(y)$后，$x$为原树根，$y$打通到了最顶上的点（不一定是原树根）

• 若$x,y$间联通，则$getroot(y)=x$

• 所以询问$getroot(y)=x?$即可

---

code

bool judge(int x,int y)
{
    makeroot(x);
    access(y);
    splay(x,0);
    return getroot(y)==x;
}

---

Link-Cut Tree常规套路

和树剖的差不多，$LCT$的题目还是问你$x$点到$y$点间的路径路径和或者极值什么的
树剖很好做静态树的嘛

LCT怎么解决这类问题呢？

其实有常规套路

• 比如询问$x$到$y$间路径和

• $makeroot(y)$后，再$access(x),splay(x,0)$，此时$x$和$y$就在同一棵splay里了

• 然后这条路径不就任你摆布了？

---

注意事项

可以求LCA……才怪……

不考虑LCT求LCA的话会发现$LCT$ 很有某些优势

• 代码复杂度的排序，应该是倍增优、LCT稍劣一点、树剖很差

• 功能的排序当然是LCT最多、树剖少、倍增最少

突然发现LCT很好打、很好用？

• 时间复杂度的排序就是树剖最快、倍增较快、LCT龟速……

由于splay带来的巨大常数因子，$LCT$的时间大约是树剖的几倍……

比如这个

这是【ZJOI2008】树的统计
上面是树剖下面LCT，比对一下代码长度和时间

所以不要听tarjan那家伙BB说LCT时间很好
而且还有一个硬伤是求不了LCA
静态树上的两个点，LCA是唯一确定的，维护的值怎么变都没有影响LCA

splay的LCA是确定的么……
所以比赛里有动态树求LCA就赶快弃掉

---

点权、边权

由于$LCT$使用灵活的$splay$维护数据，维护点权易如反掌

怎么维护LCT的边权呢？

可能先想到的是采取树剖思想，边权看成儿子的点权

• LCT也可以这么做么？

不行
由于$LCT$的$splay$旋转，儿子旋转后就成为了父亲
那维护的权值不都乱套了？

解决方法很简单

把一条连接$x,y$的边看成一个点，再把这个点和$x,y$分别连起来
如此就可以维护LCT的边权了
必须注意要开两倍空间！

---

事实证明LCT非常好用
所以需要海量例题来让你刻骨铭心

例题1：【BZOJ2049】【luoguP2147】[SDOI2008]洞穴勘测

problem

题目描述

辉辉热衷于洞穴勘测。

某天，他按照地图来到了一片被标记为JSZX的洞穴群地区。经过初步勘测，辉辉发现这片区域由n个洞穴（分别编号为1到n）以及若干通道组成，并且每条通道连接了恰好两个洞穴。假如两个洞穴可以通过一条或者多条通道按一定顺序连接起来，那么这两个洞穴就是连通的，按顺序连接在一起的这些通道则被称之为这两个洞穴之间的一条路径。
洞穴都十分坚固无法破坏，然而通道不太稳定，时常因为外界影响而发生改变，比如，根据有关仪器的监测结果，123号洞穴和127号洞穴之间有时会出现一条通道，有时这条通道又会因为某种稀奇古怪的原因被毁。

辉辉有一台监测仪器可以实时将通道的每一次改变状况在辉辉手边的终端机上显示：

如果监测到洞穴u和洞穴v之间出现了一条通道，终端机上会显示一条指令 Connect u v

如果监测到洞穴u和洞穴v之间的通道被毁，终端机上会显示一条指令 Destroy u v

经过长期的艰苦卓绝的手工推算，辉辉发现一个奇怪的现象：无论通道怎么改变，任意时刻任意两个洞穴之间至多只有一条路径。

因而，辉辉坚信这是由于某种本质规律的支配导致的。因而，辉辉更加夜以继日地坚守在终端机之前，试图通过通道的改变情况来研究这条本质规律。
然而，终于有一天，辉辉在堆积成山的演算纸中崩溃了……他把终端机往地面一砸（终端机也足够坚固无法破坏），转而求助于你，说道：“你老兄把这程序写写吧”。

辉辉希望能随时通过终端机发出指令 Query u v，向监测仪询问此时洞穴u和洞穴v是否连通。现在你要为他编写程序回答每一次询问。
已知在第一条指令显示之前，JSZX洞穴群中没有任何通道存在。

输入输出格式

输入格式： 第一行为两个正整数n和m，分别表示洞穴的个数和终端机上出现过的指令的个数。
以下m行，依次表示终端机上出现的各条指令。每行开头是一个表示指令种类的字符串s（"Connect”、”Destroy”或者”Query”，区分大小写），之后有两个整数u和v
(1≤u, v≤n且u≠v) 分别表示两个洞穴的编号。

输出格式： 对每个Query指令，输出洞穴u和洞穴v是否互相连通：是输出”Yes”，否则输出”No”。（不含双引号）

输入输出样例

输入样例#1： 复制 200 5 Query 123 127 Connect 123 127 Query 123 127 Destroy
127 123 Query 123 127 输出样例#1： 复制 No Yes No 输入样例#2： 复制 3 5 Connect 1 2
Connect 3 1 Query 2 3 Destroy 1 3 Query 2 3 输出样例#2： 复制 Yes No 说明

数据说明

10%的数据满足n≤1000, m≤20000

20%的数据满足n≤2000, m≤40000

30%的数据满足n≤3000, m≤60000

40%的数据满足n≤4000, m≤80000

50%的数据满足n≤5000, m≤100000

60%的数据满足n≤6000, m≤120000

70%的数据满足n≤7000, m≤140000

80%的数据满足n≤8000, m≤160000

90%的数据满足n≤9000, m≤180000

100%的数据满足n≤10000, m≤200000

保证所有Destroy指令将摧毁的是一条存在的通道

本题输入、输出规模比较大，建议c\c++选手使用scanf和printf进行I\O操作以免超时

---

analysis

• ……智障题

• 这题是最普通的link、cut操作和判断联通

• $makeroot(x),access(y)$后，判断$getroot(y)=x?$即可

• 不要告诉我说不知道怎么link和cut

---

code

#include
#define MAXN 30001

using namespace std;

int t[MAXN][2];
int b[MAXN],fa[MAXN],pf[MAXN],st[MAXN];
char s[10];
int n,m;

struct node 
{
    int val,sum,mx,size;
    bool rev;
}a[MAXN];

int read()
{
    int x=0,f=1;
    char ch=getchar();
    while (ch<'0' || '9'<ch)
    {
        if (ch=='-')f=-1;
        ch=getchar();   
    }
    while ('0'<=ch && ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}

void reverse(int x) 
{
    if(x)
    {
        a[x].rev^=1;
        swap(t[x][0],t[x][1]);
    }
}

void down(int x) 
{
    if (a[x].rev) 
    {
        reverse(t[x][0]),reverse(t[x][1]);
        a[x].rev=0;
    }
}

void update(int x) 
{
    if (x)
    {
        a[x].size=a[t[x][0]].size+a[t[x][1]].size+1;
    } 
}

void downdata(int x) 
{
    st[0]=0;
    while (x)st[++st[0]]=x,x=fa[x];
    while (st[0])down(st[st[0]--]);
}

int lr(int x)
{
    return t[fa[x]][1]==x;
}

void rotate(int x) 
{
    int y=fa[x],k=lr(x);
    t[y][k]=t[x][!k];

    if (t[x][!k])fa[t[x][!k]]=y;
    fa[x]=fa[y];

    if (fa[y])t[fa[y]][lr(y)]=x;    
    t[x][!k]=y;

    fa[y]=x,pf[x]=pf[y];
    update(y),update(x);
}

void splay(int x, int y) 
{
    downdata(x);
    while (fa[x]!=y)
    {
        if (fa[fa[x]]!=y)
        {
            if (lr(x)==lr(fa[x]))rotate(fa[x]); 
            else rotate(x);
        } 
        rotate(x);
    }
}

void access(int x) 
{
    for (int y=0;x;update(x),y=x,x=pf[x])
    {
        splay(x,0);
        fa[t[x][1]]=0;
        pf[t[x][1]]=x;
        t[x][1]=y;
        fa[y]=x;
        pf[y]=0;
    }
}

void makeroot(int x) 
{
    access(x); 
    splay(x,0); 
    reverse(x);
}

void link(int x,int y) 
{
    makeroot(x); 
    pf[x]=y;
}

void cut(int x,int y) 
{
    makeroot(x); 
    access(y);
    splay(x,0);
    t[x][1]=fa[y]=pf[y]=0;
    update(x);
}

int getroot(int x)
{
    while (fa[x])x=fa[x];
    return x;
}

bool judge(int x,int y)
{
    makeroot(x);
    access(y);
    splay(x,0);
    return getroot(y)==x;
}

int main()
{
    n=read(),m=read();
    while (m--)
    {
        scanf("%s",&s);
        int x=read(),y=read();
        if (s[0]=='C')link(x,y);
        else if (s[0]=='D')cut(x,y);
        else (judge(x,y))?(printf("Yes\n")):(printf("No\n"));
    }
}

---

例题2：【luoguP3203】 [HNOI2010]弹飞绵羊

problem

题目描述

某天，Lostmonkey发明了一种超级弹力装置，为了在他的绵羊朋友面前显摆，他邀请小绵羊一起玩个游戏。游戏一开始，Lostmonkey在地上沿着一条直线摆上n个装置，每个装置设定初始弹力系数ki，当绵羊达到第i个装置时，它会往后弹ki步，达到第i+ki个装置，若不存在第i+ki个装置，则绵羊被弹飞。绵羊想知道当它从第i个装置起步时，被弹几次后会被弹飞。为了使得游戏更有趣，Lostmonkey可以修改某个弹力装置的弹力系数，任何时候弹力系数均为正整数。

输入输出格式

输入格式： 第一行包含一个整数n，表示地上有n个装置，装置的编号从0到n-1。

接下来一行有n个正整数，依次为那n个装置的初始弹力系数。

第三行有一个正整数m，

接下来m行每行至少有两个数i、j，若i=1，你要输出从j出发被弹几次后被弹飞，若i=2则还会再输入一个正整数k，表示第j个弹力装置的系数被修改成k。

输出格式： 对于每个i=1的情况，你都要输出一个需要的步数，占一行。

输入输出样例

输入样例#1： 复制 4 1 2 1 1 3 1 1 2 1 1 1 1 输出样例#1： 复制 2 3 说明

对于20%的数据n,m<=10000，对于100%的数据n<=200000,m<=100000

---

analysis

• LCT板子题

• 我们可以建一个$n+1$号节点，$x$号节点连到表示$n+1$号节点就表示被弹飞

• 若要更改，直接先$cut$再$link$一波，关键怎么询问弹飞几次呢？暴力splay？

• 我们可以$makeroot(n+1)$，使$n+1$号节点变为原LCT的根

• 接着我们$access(x)$后$splay(x,0)$，也就是把$x$旋转到原树的根

• 那么$x$号节点会弹$x_{size}-1$次被弹飞，但是为什么呢？

• 由于辅助树按照深度关键字排序，所以x的子树大小-1就是要被弹飞几次了

• 所以明显正确

---

code

#include
#include
#define MAXN 200001

using namespace std;

int t[MAXN][2];
int b[MAXN],fa[MAXN],pf[MAXN],st[MAXN];
int n,m;

struct node 
{
    int size,rev;
}a[MAXN];

int min(int x,int y) 
{
    return x<y?x:y;
}

void swap(int &x,int &y)
{
    int z=x;
    x=y;
    y=z;
}

void reverse(int x) 
{
    if(x)
    {
        a[x].rev^=1;
        swap(t[x][0],t[x][1]);
    }
}

void down(int x) 
{
    if (a[x].rev) 
    {
        reverse(t[x][0]),reverse(t[x][1]);
        a[x].rev=0;
    }
}

void update(int x) 
{
    if(x)
    {
        a[x].size=a[t[x][0]].size+a[t[x][1]].size+1;
    } 
}

void downdata(int x) 
{
    while (x)st[++st[0]]=x,x=fa[x]; 
    while (st[0])down(st[st[0]--]);
}

int lr(int x) 
{
    return t[fa[x]][1]==x;
}

void rotate(int x) 
{
    int y=fa[x],k=lr(x);
    t[y][k]=t[x][!k]; 
    if(t[x][!k])fa[t[x][!k]]=y;
    fa[x]=fa[y];
    if(fa[y])t[fa[y]][lr(y)]=x;    
    t[x][!k]=y; 
    fa[y]=x; 
    pf[x]=pf[y];
    update(y),update(x);
}

void splay(int x, int y) 
{
    downdata(x);
    while(fa[x]!=y)
    {
        if(fa[fa[x]]!=y)
        {
            if(lr(x)==lr(fa[x]))rotate(fa[x]); 
            else rotate(x);
        } 
        rotate(x);
    }
}

void access(int x) 
{
    for (int y=0;x;update(x),y=x,x=pf[x])
    {
        splay(x,0);
        fa[t[x][1]]=0;
        pf[t[x][1]]=x;
        t[x][1]=y;
        fa[y]=x;
        pf[y]=0;
    }
}

void makeroot(int x) 
{
    access(x); 
    splay(x,0); 
    reverse(x);
}

void link(int x,int y) 
{
    makeroot(x); 
    pf[x]=y;
}

void cut(int x,int y) 
{
    makeroot(x); 
    access(y);
    splay(x,0);
    t[x][1]=fa[y]=pf[y]=0;
    update(x);
}

int main() 
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++) 
    {
        scanf("%d",&b[i]);
        link(i,min(n+1,i+b[i]));
    }
    scanf("%d",&m);
    while (m--)
    {
        int z,x; 
        scanf("%d%d",&z,&x),x++;
        if (z==1) 
        {
            makeroot(n+1);
            access(x);
            splay(x,0);
            printf("%d\n",a[x].size-1);
        } 
        else 
        {
            cut(x,min(x+b[x],n+1));
            scanf("%d",&b[x]);
            link(x,min(x+b[x],n+1));
        }
    }
}

---

例题3：【JZOJ2256】【ZJOI2008】树的统计

problem

题目上面有所以就不重新贴了

---

analysis

• 前面是用树剖做的，现在用LCT重做了一次

• 其实LCT的代码复杂度简直秒杀树剖好伐

• 都说了LCT能做所有树剖题，然而这题连cut操作都没有

• 那不就简单了？

• 像普通套路一样，询问$x,y$间的路径极值或权值和，就$makeroot(y),access(x),splay(x,0)$

• 然后直接输出$a[x]{.}_{XXX}$就好了

• 至于修改$x$节点的操作，把$x$旋到根，直接修改即可

然而WA90

• 为什么呢？

• 每次输入的时候，都要把当前节点旋到根，读入后再$update$

• 这样才终于切了

---

code

#include
#define MAXN 30001

using namespace std;

int t[MAXN][2];
int b[MAXN],fa[MAXN],pf[MAXN],st[MAXN];
char s[10];
int n,m;

struct node 
{
    int val,sum,mx,size,rev;
}a[MAXN];

int read()
{
    int x=0,f=1;
    char ch=getchar();
    while (ch<'0' || '9'<ch)
    {
        if (ch=='-')f=-1;
        ch=getchar();   
    }
    while ('0'<=ch && ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}

void reverse(int x) 
{
    if(x)
    {
        a[x].rev^=1;
        swap(t[x][0],t[x][1]);
    }
}

void down(int x) 
{
    if (a[x].rev) 
    {
        reverse(t[x][0]),reverse(t[x][1]);
        a[x].rev=0;
    }
}

void update(int x) 
{
    if (x)
    {
        a[x].size=a[t[x][0]].size+a[t[x][1]].size+1;
        a[x].sum=a[x].val+a[t[x][0]].sum+a[t[x][1]].sum;
        a[x].mx=max(a[x].val,max(a[t[x][0]].mx,a[t[x][1]].mx));
    } 
}

void downdata(int x) 
{
	st[0]=0;
    while (x)st[++st[0]]=x,x=fa[x]; 
    while (st[0])down(st[st[0]--]);
}

int lr(int x)
{
    return t[fa[x]][1]==x;
}

void rotate(int x) 
{
    int y=fa[x],k=lr(x);
    t[y][k]=t[x][!k];
    
    if (t[x][!k])fa[t[x][!k]]=y;
    fa[x]=fa[y];
    
    if (fa[y])t[fa[y]][lr(y)]=x;    
    t[x][!k]=y;
    
    fa[y]=x,pf[x]=pf[y];
    update(y),update(x);
}

void splay(int x, int y) 
{
    downdata(x);
    while (fa[x]!=y)
    {
        if (fa[fa[x]]!=y)
        {
            if (lr(x)==lr(fa[x]))rotate(fa[x]); 
            else rotate(x);
        } 
        rotate(x);
    }
}

void access(int x) 
{
    for (int y=0;x;update(x),y=x,x=pf[x