BM算法
BM算法
BM算法就是这样的一个算法。首先它和KMP算法一样都是从主串的最左端开始,然后不断右移的:
不同之处在于,BM算法每次判断匹配时是从右往左比较的。
下面给出的是一个简单的后缀比较的BF算法,而它和BM算法的区别就在于++patAt的不同:
int postfixBfMatch(const string & text, const string & pat)
{
//patAt指向了当前pat和text对齐的位置
int patAt = 0;
int cmp;
const size_t PATLAST = pat.length() - 1;
while (patAt + pat.length() <= text.length())
{
cmp = PATLAST;
//如果匹配成功,cmp就会来到-1的位置上
for (cmp = PATLAST; cmp >= 0 && pat[cmp] == text[patAt+cmp]; --cmp);
if (cmp == -1)
break;
else
++patAt;
}
return patAt;
}我们对BM算法的实现就是从对以上程序的优化开始的。
坏字符
我们现在将匹配过程中,主串失配位置的字符称之为“坏字符”。根据这个坏字符,我们可以“总结出一些教训”,进而改进以上的算法。
![]()
基本思路
显然当我们遇到了坏字符的时候,就需要移动模式串。问题是要移动多少呢?
考虑两种情况:
1. 坏字符不存在于模式串的集合中
这是我们非常乐于看到的情况。试想如果出现这种情形,那么就意味着模式串不可能与该字符的位置有任何重合。在这种情况下,我们只需将整个模式串都移动到该坏字符之后的位置就行了。
![]()
- 坏字符存在于模式串的集合中
这种情况略有些复杂。一般我们的做法是找到模式串里从右往左第一个和这个坏字符匹配的字符,然后移动模式串让该字符和坏字符对齐。
不过这样做有一个问题,因为显然这样可能造成模式串倒退移动。但是我们仔细分析,显然如果遇到了要倒退的情况,那么肯定不可能是我们要找的匹配位置。因为模式串是从左向右移动匹配的,所以在任意比较位置之前的位置都不可能是目标位置。
为了解决这个问题,我们也可以做一个小修改,如果检测到要位移量会小于零,那我们就右移一位(后面会看到,还有更好的办法)。
![]()
bc表
那么要怎么移动呢?又如何确定遇到坏字符的时候,要向右移动多少呢?
首先来看第一个问题。首先明确一点,基于我们之前给出的程序框架中两个指针分别为patAt和cmp,我们最好不要像KMP算法中那样直接改变cmp的值。更好的办法是直接给出位移量,然后移动patAt:
patAt += motion motion是多少呢?显然它应该是cmp到模式串中和坏字符相同的最右端的字符位置的距离。即:
motion = cmp - location(badchar) 但还有一个问题,如果坏字符不存在,lacation有该是什么呢?这里我们就想到了我们在KMP算法中使用的通配符了,在这里我们依然这么做。所以对于任意的nonExist坏字符不属于模式串的集合,则有:
location(nonExist) = -1; 仔细计算一下,我们就会发现,这种情况下,刚好能够让整个模式串调到坏字符的下一位。
那么这样一来,我们就只剩下一个最关键的问题了:location要怎么求得?难道要写一个以char为参数返回int的函数?
我们仔细观察一下,就会发现location的值只和模式串本身有关,这让我们不禁想到了可以像KMP一样预先构建一个表——在这里我们称之为bc表。但是问题没那么简单,因为在这里,输入的badchar的种类范围极多,不可能构建出一个像next表那样的简单的数组表。所以这里我们就可以看到该算法的一个关键思路:那就是构造一个以字符本事为键值的hash表,凡是存在与模式串中的字符对应的位置的值都是该字符最后一次出现的位置;其余不想管字符,如我们之前所言,通通置为-1。具体算法如下:
int * getBc(const string & pattern)
{
//256是字符表的规模大小(ACSII)
int *bc = new int[256];
int len = pattern.length();
for (int i = 0; i < 256; ++i)
bc[i] = -1;
for (int i = 0; i < len; ++i)
{
bc[pattern[i]] = i;
}
return bc;
} 由于字符本质上还是int类型,我们可以很方便地用数组来实现hash表。这里我们将hash表的尺寸置为ASCII码表的规模——256,然后同一赋值为-1。
接下来,我们遍历模式串,每个字符本身就是它的哈希码,它的索引则是保存的值。注意这里很有技巧性的一点是我们是从左往右遍历的。这样的好处就在于即使模式串中存在相同的字符,后来的字符也会用自己的索引值覆盖掉之前赋予的值。
bc表的值代表了给定的字符在模式串上最后一次出现的位置。
对于不存在的字符,假定模式串前面还有一个通配符,任何字符都可以在哪里出现。
做完了这些工作,我们就可以利用这张bc表来优化算法了:
int bmMatch(const string & text, const string & pat)
{
int *bc = getBc(pat);
//patAt指向了当前pat和text对齐的位置
int patAt = 0;
//cmp指向了当前比较的位置
int cmp;
const size_t PATLASTID = pat.length() - 1;
const size_t patLen = pat.length();
const size_t textLen = text.length();
while (patAt + patLen <= textLen)
{
//如果匹配成功,cmp就会来到-1的位置上
//patAt + cmp 指向了text上当前比较的字符
for (cmp = PATLASTID; cmp >= 0 && pat[cmp] == text[patAt + cmp]; --cmp);
if (cmp == -1)
break;
else
{
int span = cmp - bc[text[patAt + cmp]];
patAt += (span > 0)? span : 1;
}
}
delete[] bc;
return (patAt + patLen <= textLen)? patAt : -1;
}坏字符算法评估
- 最佳情况:
$O(m/n)$
考虑下面这种情况,显然每次比对,模式串都会直接跳过4个位置。在类似于这种情况的情形下,BM算法格外优秀。
更一般的说,如果匹配的时候失配的概率越高,BM的表现越优秀。所以,BM算法更适用于在字符规模较大的情形下(ASCII, Unicode)。
xxx1xxx1xxx1···xxx1
0000- 最坏情况:
$O(mn)$
很遗憾的是仅靠坏字符算法,也可能会变得效率极为低下。比如这种情况:
0000000····0000
1000仔细观察,你就会发现在以上的情况下,算法的执行流程完全等同于BF算法。效率极为低下的原因在于该算法完全无视了之前存在部分匹配的事实。所以仅有坏字符策略是不够的,再次基础上我们还要在加上其他的一些策略。
好后缀
基本思路
在有了坏字符的基础上我们还要加上所谓的“好后缀”策略。所谓好后缀就是从后往前匹配部分的后缀。简而言之即是坏字符对应的位置后面一段的后缀。
和KMP算法一样,有了好后缀我们也要移动模式串,来达到依旧部分匹配的目标。而移动的情况分为三种:
1. 模式串中有子串匹配上好后缀
显然,这是只需要移动模式串知道子串和好后缀重合就行了
![]()
- 模式串中没有子串匹配上后后缀,但存在一个最长前缀,它等于好后缀的后缀
![]()
- 模式串中没有子串匹配上后后缀,并且在模式串中找不到最长前缀
这种情况是我们最喜欢的了:直接整个全部移走
![]()
gs表
有了之前的经验,我们很容易找到移动的方法:事先构建一个表单,上面记录了每次需要移动的距离。我们将这个表称之为gs表。
但是gs表想要直接构建是比较困难的。具体实现的时候我们会使用一个叫做suffix表的辅助表。
构建suffix
suffix表是一个这样的表:
suffix[i] = s表示以i为边界,与模式串后缀匹配的最大长度,如下图所示,用公式可以描述:满足P[i-s, i] == P[m-s, m]的最大长度s。
![]()
构建算法较为简单:
int * suffixes(const string & pat)
{
const int len = pat.length();
int num;
int *suff = new int[len];
suff[len - 1] = len;
for (int i = len - 2; i >= 0; --i)
{
for (num = 0; num <= i && pat[i-num] == pat[len-num-1]; ++num);
suff[i] = num;
}
return suff;
}构建gs
有了suffix表之后,我们就可以构建gs表了。
gs[i]表示遇到好后缀时,模式串应该移动的距离,其中i表示好后缀前面一个字符的位置(也就是坏字符的位置)
构建bmGs数组分为三种情况,分别对应上述的移动模式串的三种情况:
- 模式串中有子串匹配上好后缀
![]()
- 模式串中没有子串匹配上好后缀,但找到一个最大前缀
![]()
- 模式串中没有子串匹配上好后缀,但找不到一个最大前缀
![]()
再给出具体实现之前,首先让我们来考虑这样一个问题:如果同时存在符合条件的串中子串和前缀子串我们优先考虑那个呢?答案不言而喻:为了防止回溯,我们应该尽量让一次移动的距离少一点。所以如果有多种匹配情况:优先匹配串中子串,其次是最大前缀,最后再是移动整个模式串。
int * getGs(const string & pat)
{
const int len = pat.length();
const int lastIndex = len - 1;
int *suffix = suffixes(pat);
int *gs = new int[len];
//找不到对应的子串和前缀
for (int i = 0; i < len; ++i)
gs[i] = len;
//找前缀
for (int i = lastIndex; i >= 0; --i)
{
//存在我们想要的前缀
if (suffix[i] == i + 1)
{
for (int j = 0; j < lastIndex - i; ++j)
{
if (gs[j] == len)
gs[j] = lastIndex - i;
}
}
}
//找中间的匹配子串
for (int i = 0; i < lastIndex; ++i)
{
gs[lastIndex - suffix[i]] = lastIndex - i;
}
delete[] suffix;
return gs;
} 以上就是gs表构建的具体算法。我们注意到算法的核心部分其实是三个for循环,分别对应了:找不到对应的子串和前缀,找到了前缀,找到了中间匹配的子串。
这里的技巧在于 for循环的安排顺序是不可调换的。注意到:如果gs[i]在三个循环流程中都有设计,那么gs[i]的值必然越来越小。通过这种安排我们就可以保证如果有在位置i有多种移动方式,那么gs[i]给出的方案一定是移动量最小的。
在对整体的安排有了一个分析后,我们来具体分析每个循环算法中的功效。
第一个for循环对应了移动整个模式串
for (int i = 0; i < len; ++i)
gs[i] = len; 可以看到我们在这里将整个gs表都赋值为len。这是一个巧妙的处理,因为如果在i处还有更好的移动方案,那么gs[i]在后面的处理中一定会被覆盖掉。而如果不被覆盖,那就说明这种移动是合理的。例如在下图的字符a处,我们发现只要文本串中后缀对应部分还和模式串重合,就不可能匹配,所以之间将模式串移走整个距离就可以了。
![]()
第二个for循环对应了找到了一个最大前缀
for (int i = lastIndex; i >= 0; --i)
{
//存在我们想要的前缀
if (suffix[i] == i + 1)
{
for (int j = 0; j < lastIndex - i; ++j)
{
if (gs[j] == len)
gs[j] = lastIndex - i;
}
}
}这个算法较为复杂,下面展开细节分析:
判断前缀的存在性
这里的技巧在于如何判断前缀存在?答案是如果 suffix[i] = i+1那就说明存在这样一个前缀。所以判断条件:
for (....)
{
if (suffix[i] == i + 1)
{
}
}的含义就是 遍历整个模式串,一旦找到了符合前缀要求的字符就执行内部的逻辑(即填值上去)。
从后往前
我们注意到一个很奇怪的现象,是出在最外面的for身上:
for (int i = lastIndex; i >= 0; --i) 为什么从后往前遍历?
我们要考虑到一点:如果存在 $i$ 和 $j$ 且 $i > j$ 都满足前缀的要求,我们选哪个?显然我们沿用刚才的思路:我们不希望一次性移动太多距离,所以如果有多个符合的选项选择能让移动距离最小的。

既然我们希望最终的结果是指向前缀的最后一个字符,那么我们就可以有两种办法:
- 从前往后遍历,用后来者覆盖前面的内容
- 从后往前遍历,并想办法阻止覆盖操作
仔细比较,我们选择了后者。因为如果最大前缀很长的话,我们就会被迫执行大量垃圾操作,这回极大地影响算法的效率。而关于后者如何阻止覆盖,我们稍后再讲。
这样我们就来到了最内层的区域:
for (int j = 0; j < lastIndex - i; ++j)
{
if (gs[j] == len)
gs[j] = lastIndex - i;
}填表操作
首先解释一下最里层的运算,也就是真正意义上的填表操作:
gs[j] = lastIndex - i;![]()
为什么是lastIndex-i我们可以从上图中得出答案。不再赘述。
找到了前缀的模式串和执行相关操作的区间
接着我们从外向内讲。首先就是又一重的循环:
for (int j = 0; j < lastIndex - i; ++j) 这重循环的含义在于覆盖所有位于这块区间的gs[j]的值,让所有在该区间失配的情况下都像右移动lastIndex - i个单位。这里有两个略微需要转个弯才想明白的问题。
- 为什么失配在不同地方却移动相同的距离?
首先,我们要明确,这只是整体处理的一个步骤。这意味着如果我们还可以找到串中子串的话,那么gs[j]值待会还要被覆盖。那么如果只能找到最大前缀的话,那他们移动的距离也都相同?
答案是是的。因为在这种情况下,只要失配的位置在目标后缀的第一个字符之前。那么具体位置毫无意义。因为根本不可能找到一个和该失配字符之后的整个后缀完全匹配的子串,所以不论停在那里,最终都只能把模式串右移lastIndex-i个单位,来让最大前缀和目标后缀对应的文本串中的子串相重合。
以下图为例,这里我们停在了字符g的位置,但这有用吗?模式串中根本不存在一个bcde的子串,只有一个cde的前缀。所以不论是停在了g处还是在f或者e处都没有区别,最终都只能移动模式串知道前缀cde和文本串中的cde匹配。换而言之——移动距离相同。
![]()
- 为什么
j < lastIndex - i?
在上一点的分析中我们有提到过这样一句话:
“只要失配的位置在目标后缀的第一个字符之前”。
事实上这句话就对应了j < lastIndex - i,意思是,我们的操作仅限于目标后缀之前的字符。因为目标后缀中的字符必然可以找到与自己的后缀像匹配的子串。
阻止覆盖
前面我们讲到,为了维护算法的效率,我们选择从后往前遍历。但这会带来一个问题,就是可能存在期望值被覆盖的可能。这就要用到我们的判断条件了:
if (gs[j] == len)事实上,我们还可以有其他的手段,这里就不再讲了。
第三个for循环对应了找到一个串中子串
for (int i = 0; i < lastIndex; ++i)
{
gs[lastIndex - suffix[i]] = lastIndex - i;
}首先先看最里面的执行操作:
gs[lastIndex - suffix[i]] = lastIndex - i; lastIndex - i好理解,就是要移动的距离。
![]()
lastIndex - suffix[i]就很有技巧性了,它对应的位置如上图所示,下图是简化版:
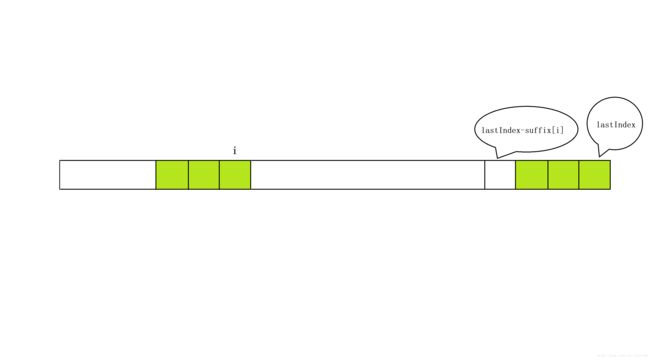
结合外层的循环:
for (int i = 0; i < lastIndex; ++i)
{
} 我们就可以大致看出该算法的执行逻辑:从头到尾遍历模式串,依次找到合适的位置,将然后填充其他位置的gs值。我们来分析具体的细节:
- 遍历的顺序必须是从左到右
有了前面的基础,这个规则就很好理解了。简而言之如果lastIndex-suffix[i] == lastIndex-suffix[j]且$i。从而保证了我们一直坚持的尽量不回溯的原则。 lastIndex - j覆盖移动距离大的lastIndex - i
- 最后一位没有列入循环
注意到我们的循环条件i < lastIndex,也就是收最后一位并没有处理。这是因为suffix[lastIndex] == length,所以处理了也毫无意义。
- 如果suffix[i] == 0
这种情况下意味着pat[i] != pat[lastIndex]那就至少需要将pat移动到一个使新比较的字符和之前的字符不同的位置。
改进BM主算法
有了好后缀之后,我们就可以改进主算法了:
patAt += max(gs[cmp], cmp - bc[text[patAt + cmp]]); 由于gc[cmp]必定大于零,所以就可以避免了使用bc表时后退的情况。
同时由于两者的移动都是合理的,所以我们不妨选择在合理范围内更加大的移动量以提高算法效率。(注意此前我们强调要让移动距离尽可能小是因为无法确定更大的移动是否是合理的)。
最终算法
int bmMatch(const string & text, const string & pat)
{
int *bc = getBc(pat);
int *gs = getGs(pat);
//patAt指向了当前pat和text对齐的位置
int patAt = 0;
//cmp指向了当前比较的位置
int cmp;
const size_t PATLASTID = pat.length() - 1;
const size_t patLen = pat.length();
const size_t textLen = text.length();
while (patAt + patLen <= textLen)
{
//如果匹配成功,cmp就会来到-1的位置上
//patAt + cmp 指向了text上当前比较的字符
for (cmp = PATLASTID; cmp >= 0 && pat[cmp] == text[patAt + cmp]; --cmp);
if (cmp == -1)
break;
else
{
patAt += max(gs[cmp], cmp - bc[text[patAt + cmp]]);
}
}
delete[] bc;
delete[] gs;
return (patAt + patLen <= textLen)? patAt : -1;
}
int * getBc(const string & pattern)
{
//256是字符表的规模大小(ACSII)
int *bc = new int[256];
int len = pattern.length();
for (int i = 0; i < 256; ++i)
bc[i] = -1;
for (int i = 0; i < len; ++i)
{
bc[pattern[i]] = i;
}
return bc;
}
int * suffixes(const string & pat)
{
const int len = pat.length();
int num;
int *suff = new int[len];
suff[len - 1] = len;
for (int i = len - 2; i >= 0; --i)
{
for (num = 0; num <= i && pat[i-num] == pat[len-num-1]; ++num);
suff[i] = num;
}
return suff;
}
int * getGs(const string & pat)
{
const int len = pat.length();
const int lastIndex = len - 1;
int *suffix = suffixes(pat);
int *gs = new int[len];
//找不到对应的子串和前缀
for (int i = 0; i < len; ++i)
gs[i] = len;
//找前缀
for (int i = lastIndex; i >= 0; --i)
{
//存在我们想要的前缀
if (suffix[i] == i + 1)
{
for (int j = 0; j < lastIndex - i; ++j)
{
if (gs[j] == len)
gs[j] = lastIndex - i;
}
}
}
//找中间的匹配子串
for (int i = 0; i < lastIndex; ++i)
{
gs[lastIndex - suffix[i]] = lastIndex - i;
}
delete[] suffix;
return gs;
}