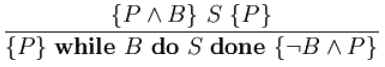八卦一下模型验证(一)
先穿渔网袜从珠穆朗玛峰上滚下来哭求CSDN的大大们看一下CSDN博客插件不能自动上传图片和排版的问题。人肉上传图片和排版真地很痛苦呐!
2007图灵奖和模型检验
不知道长达半年的疯狂加班是否损害了自己的心理健康。回顾过去几个月,似乎除了工作嘛都没干。人仿佛颓了,觉得时光了无意义地飞逝,过去半年的泰半记忆好像盛夏阳光里的冰块,蒸发得不剩一丝水汽。幸好不是全无亮点,比如看到好朋友幸福无比地结婚。中学好友到家里盘桓月余,也是一大快事。Steve McConnell在Rapid Development里的案例分析里提到death march之后程序员往往大批离开。想不到这次亲自体会了一把,人生又完整了一点。过去几周一系列戏剧性的事件让我仔细思考了一下激励团队士气的问题,也算小小的收获。
跑题了。本来想说什么来着?对了,图灵奖和模型检验。2007年的图灵奖授予Edmund M. Clarke, E. Allen Emerson, and Joseph Sifakis,表彰他们在模型验证方面做出的开创性贡献。前段时间白天忙项目,晚上改简和历准备面试,也就没有心情八卦。刘江老师在他的博客里做了详细介绍,在这里推荐一下。关于几位大牛,俺没有什么补充的,就八卦一下他们的研究方向:模型检验。
模型检验是计算机科学理论与实践结合的经典范例,背后也有一段跌宕起伏、绝处逢生的历史。八卦这段历史前,我们得知道什么是模型验证,以及为什么它为什么重要到能得图灵奖。在CS理论里,一个模型就是一个数学结构,比如有向图,或者状态机。我们往往希望知道一个结构是否符合一定的性质。这些性质可以用逻辑公式表达。比如下面的有向图G(V, E)里,V代表所有节点的集合,{A, B, C, D, E}, 而E代表所有路径的集合{(A, B), (B, C), (D, C), (B, D), (D, B), (E, D), (B, E)}。如果如果我们想验证G里没有从A到C的直接路径,但有经过一个节点的间接路径,就可以验证下面这个公式在G里面为真。
简单解释一下:
- 这种式子叫Tableau。如果分数线上的式子成立,则推断分数线下的式子也成立。
- {P . B} S {P}即Hoare三段式(Hoare Triple),意思是如果条件P和B在程序S执行前为真,且程序S运行中止,那么条件P在S结束运行后依然为真。
- {P} while B do S done {×B . P}的意思是如果P在执行while循环前成立,且循环while B do S done能退出,那么循环退出后B不再为真,而P依然为真。这里的P有坨专门称呼:循环不变量,loop invariant。B也有个诨名,循环护卫,loop guard。
- 从这个式子可以看出,要证明一段循环的结果正确,我们只需找出循环不变量P,然后再证明两件事:这段循环可以结束,也就是loop guard能从真值最终变为假,而不变量P一直为真。
不过,验证程序的思想并没有兴盛起来。原因挺简单:用基于演绎的方法从基本的定理出发证明整个程序也忒难了。仅仅是找到合适的不变量就足以让我等凡人抓狂。Dijkstra一辈子都呼吁编程应像推导数学定理一样严谨,否则遗患无穷。可总不能要求人人都是戴爷爷级别的牛人吧?何况就算戴爷爷,只怕也难证明几千行的驱动程序没有死锁。一直到70年代,程序证明在工业界也没有什么真正的影响。当然这不是说系统验证这门学科失去活力。事实上当时Tony Hoare,E.W., Dijkstra,E.A. Ashcroft, David Gries,Robert Floyd等一票大牛们在形式理论上突飞猛进,深入研究了程序的公理化证明,并行程序的断言证明,程序的推导和不可确定性等一系列课题。自动定理证明也做得有声有色。这些东西为日后花样繁多的自动程序验证奠定了基础。
眼见实践方面山穷水尽,以色列的Amir Pnueli 从澡盆里跳出来了:解决问题之道不在完美方案,而在确定可以解决的问题,以及合适的切入角度。有时候放弃是福。好比当年Multics的老大硬要用几十页汇编自动解决context switching时的PC-losering问题,结果搞得代码维护异常困难。但Dennis Ritche为了实现的简单,干脆放弃自动维护,把这个问题交给程序员。以后的故事就是历史乐。验证任意系统的正确性太难,就验证状态有限的reactive系统嘛。各式硬件和嵌入系统可都是reactive系统。好像用有限状态机也能完善地描述。既然验证整个程序太难,就验证程序的某些特性嘛。大家都觉得测试比证明省钱,我们就专挑测试搞不定的方面嘛。关键数据会溢出么?浮点计算会出错么?安全协议有漏洞么?关键数据会被破坏么?每条进程都能在规定时间内被执行么?这些好像应用面挺广,也能用逻辑公式相对容易地描述。测试单写多读的玩具并行程序当然比证明简单。但是发现1962年让Mariner I Space Probe坠毁大西洋的计算错误呢?1986年让Therac-25过量辐射X射线致死病人的错误呢?1995年导致Intel大规模回收芯片的浮点错误呢?1996年导致阿里亚娜5号火箭坠毁的整数溢出错误呢?
系统的状态随时间而变,更不必说并发系统的状态同程序执行的时机紧密相连。当我们开始研究程序的行为,而不仅是程序的输入输出时,就不可避免同时间打交道。因此,我们需要一套全新的工具,不仅能简洁地描述系统的时态,还不用陷入对具体时间的琐碎处理。目光锐利的Pnuelli看上了时序逻辑。于是1977年,开创性的论文,Temporal Logics of Programs(程序的时序逻辑),问世乐。Pnuelli在论文里提出用时序逻辑证明程序的正确性。时序逻辑历史悠久,亚里士多德就对一阶二元谓词逻辑做过不少研究。它的关键思想是把时间看作一系列离散的状态。状态间的传递等同于时间的延续。Pnuelli提出的是线性时序逻辑(Linear Temporal Logic, LTL)。LTL在一阶命题逻辑的基础上引入了几坨与时间有关的操作符。
抛开命题逻辑的黑话,我们每天都用到命题逻辑,无非就是把逻辑陈述用逻辑操作符连接起来。下面的例子是一坨命题表达式:×(i > 0 . i < 10) 其中i>0和i<10是陈述(statement),符号×是操作符逻辑非,相当于C里的!,中间的.是逻辑与的操作符,相当于C里的&&。命题逻辑的局限在于它导出的真相一成不变。比如在华为这个世界里(黑话叫model或者domain或者world,看你怎么归类了),陈述“加班就是好”永远是对的,不管是项目吃紧的时候,还是项目符合进度的时候,哪怕有人累死,有人宁愿跳楼也不跳槽,有人写出2000行的函数,有人连熬几十小时后回家睡觉也算旷工,这个陈述都为真。那我们要表达“总有某个时候,加班不好”就没辄了。为了解决这个问题,LTL就在命题逻辑的基础上加入了时序操作符:
- G:表示永远为真。比如G(i < 0)表示i在任意时间都小于0。
- F:表示最终为真。比如F(i < 0)表示i在某个时间一定小于0(但现在不一定小于0)。
- X:表示下一个时刻为真。比如X(i < 0)表示时钟跳到下一个时刻,i就必须小于0。
- U:表示直到某刻前一直为真。比如(i < 0) U (j < 0)表示i一直小于0,直到j变得小于0。
- R:表示到了某刻才为真。比如(i < 0) R (j < 0)表示j 一直小于0,直到某个时刻i变得小于0。
其实{G, F, X}中任取一个,{U,R}中任取一个,就足以构成完备的LTL操作符。有兴趣的老大可以自行证明。有了这些操作符,我们就可以方便地描述系统的时态性质了。这里列举几个LTL模式库里的例子(是滴,LTL Properties Specification Patterns, 谁说搞理论的老大们不与时俱进来着?
例1:
当系统发出打开网络连接的请求后,如果遇到网络错误,必须弹出一段错误信息。我们用OpeningNetworkConnection表示网络连接的请求已经发出,用NetworkError表示网络错误被返回,而ErrorMessage表示弹出错误信息。
公式是:G(OpenNetworkConnection->G(NetworkError-> F(ErrorMessage)))
我们从内向外分析:
- NetworkError -> F(ErrorMessage)表示如果NetworError为真,那么ErrorMessage最终一定会为真。也就是说网络错误发生后,一定会在未来某个时候出现错误信息。
- G(NetworkError -> F(ErrorMessage))则表示1.陈述的性质在任何时候都要成立。
- OpenNetworkConnection –> G(NetworkError-> F(ErrorMessage))进一步说明,当网络连接打开后,我们可以肯定2.的陈述总是为真。
- 最后,G(OpenNetworkConnection->G(NetworkError-> F(ErrorMessage)))说明3.里的陈述在任何时刻都为真。
例2:
很多系统里都需要调度任务。对任意任务,我们要求把任务加入调度表前,不应该从调度表里取消该任务。我们用register表示加入任务,用unregister表示取消任务,那么公式可以写作F(register) -> (!unregister U register),意思是如果任务最终被加入调度表,我们可以推知该任务从未在加入调度表前被取消过。
虽说时序逻辑让Pnuelli得了1996年的图灵奖,工业界仍然波澜不惊。这大概是因为用时序逻辑证明程序性质依然属于从基本定理出发的演绎,难度依然太大,代价依然高昂。证明之于程序员,好比汇编之于DBA。申明式编程才是王道。我们希望给出系统的设计或实现,描述一些性质,剩下的便交给程序,让程序判断系统是否满足这些性质。如果不满足,则给出反例,以便排错。而这,正是模型验证做的事。
我们已经知道系统的性质可以用时序逻辑描述。现在还缺的,就是合适的模型,以及相配的算法。