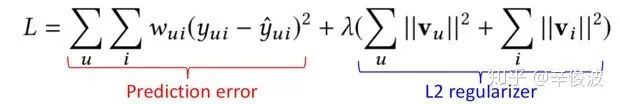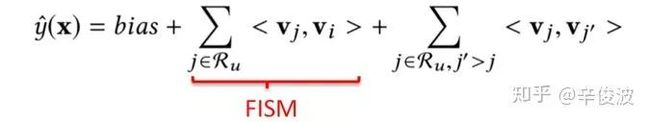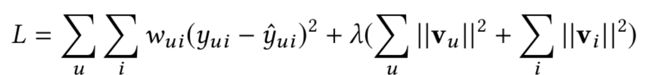搜索推荐中的召回匹配模型综述(一)：传统方法

Part0 搜索推荐中的匹配模型综述

本文主要启发来源SIGIR2018的这篇综述性slides《Deep Learning for Matching in Search and Recommendation》，重点阐述搜索和推荐中的深度匹配问题，非常solid的综述，针对里面的一些方法，尤其是feature- based的深度学习方法增加了近期一些相关paper。推荐系统和搜索应该是机器学习乃至深度学习在工业界落地应用最多也最容易变现的场景。而无论是搜索还是推荐，本质其实都是匹配，搜索的本质是给定query，匹配doc；推荐的本质是给定user，推荐item。本文主要讲推荐系统里的匹配问题，包括传统匹配模型和深度学习模型。

深度学习之风虽然愈演愈烈，但背后体现的矩阵分解思想、协同过滤思想等其实一直都是贯穿其中，如svd++体现的userCF和itemCF的思想，FM模型本质上可以退化成以上大多数模型等。多对这些方法做总结，有助于更深刻理解不同模型之间的关联。

图1 推荐和搜索的本质，都是match的过程

Part1 基于Collaborative Filtering的方法

CF模型

说到推荐系统里最经典的模型，莫过于大名鼎鼎的协同过滤了。协同过滤基于一个最基本的假设：一个用户的行为，可以由和他行为相似的用户进行预测。

协同过滤的基本思想是基于的所有交互行为，利用集体智慧进行推荐。CF按照类型可以分为3种，user-based CF、item- based CF和model-based CF。

（1）User-base CF：通过对用户喜欢的item 进行分析，如果用户a和用户b喜欢过的item差不多，那么用户a和b是相似的。类似朋友推荐一样，可以将b喜欢过但是a没有看过的item推荐给a

（2）Item-base CF: item A和item B如果被差不多的人喜欢，认为item A和item B是相似的。用户如果喜欢item A, 那么给用户推荐item B大概率也是喜欢的。比如用户浏览过这篇介绍推荐系统的文章，也很有可能会喜欢和推荐系统类似的其他机器学习相关文章。

（3）model-base CF: 也叫基于学习的方法，通过定义一个参数模型来描述用户和物品、用户和用户、物品和物品之间的关系，然后通过已有的用户- 物品评分矩阵来优化求解得到参数。例如矩阵分解、隐语义模型LFM等。

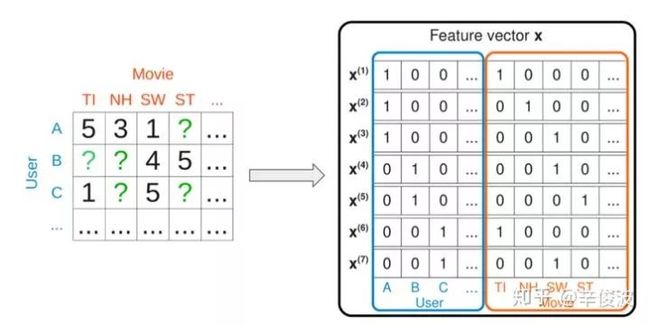
CF协同过滤的思路要解决的问题用数据形式表达就是：矩阵的未知部分如何填充问题（Matrix Completion）。如图2.1所示，已知的值是用户已经交互过的item，如何基于这些已知值填充矩阵剩下的未知值，也就是去预测用户没有交互过的item是矩阵填充要解决的问题。

图2.1 用户对左图评分过的电影，可以用右图矩阵填充表达

矩阵填充可以用经典的SVD（Singular Value Decomposition )解决，如图2.1所示

图2.2 SVD矩阵分解

其中左侧M=m*n表示用户评分矩阵，m矩阵的行表示用户数，n矩阵的列表示item数，在大多数推荐系统中m和n规模都比较大，因此希望通过将M分解成右侧低秩的形式。一般来说SVD求解可以分为三步：

（1） 对M矩阵的missing data填充为0

（2） 求解SVD问题，得到U矩阵和V矩阵

（3） 利用U和V矩阵的低秩k维矩阵来估计

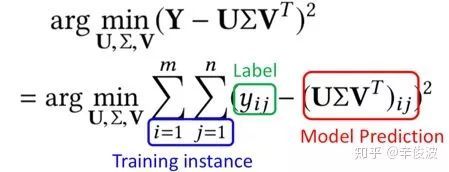
对于第二步种的SVD求解问题，等价于以下的最优化问题：

其中yij为用户i对物品j的真实评分，也就是label, U和V为模型预估值，求解矩阵U和V的过程就是最小化用户真实评分矩阵和预测矩阵误差的过程。

这种SVD求解方法存在以下问题：

（1） missing data（在数据集占比超过99%）和observe data权重一样

（2） 最小化过程没有正则化（只有最小方差），容易产生过拟合

因此，一般来说针对原始的SVD方法会有很多改进方法。

---

MF模型（矩阵分解）

为解决上述过拟合情况，矩阵分解模型（matrix factorization）提出的模型如下

MF模型的核心思想可以分成两步

（1）将用户u对物品i的打分分解成用户的隐向量vu，以及物品的隐向量vi

（2）用户u和物品i的向量点积（inner product）得到的value，可以用来代表用户u对物品i的喜好程度，分数越高代表该item推荐给用户的概率就越大

同时，MF模型引入了l2正则来解决过拟合问题

当然，这里除了用l2 正则，其他正则手段例如l1正则，cross-entropy正则也都是可以的。

---

FISM模型

上述提到的两种模型CF方法和MF方法都只是简单利用了user- item的交互信息，对于用户本身的表达是userid也就是用户本身。2014年KDD上提出了一种更加能够表达用户信息的方法，Factored Item Similarity Model，简称FISM，顾名思义，就是将用户喜欢过的item作为用户的表达来刻画用户，用数据公式表示如下：

注意到用户表达不再是独立的隐向量，而是用用户喜欢过的所有item的累加求和得到作为user的表达；而item本身的隐向量vi是另一套表示，两者最终同样用向量内积表示。

---

SVD++模型

MF模型可以看成是user-based的CF模型，直接将用户id映射成隐向量，而FISM模型可以看成是item- based的CF模型，将用户交户过的item的集合映射成隐向量。一个是userid本身的信息，一个是user过去交互过的item的信息，如何结合user- base和item-base这两者本身的优势呢？

SVD++方法正是这两者的结合，数学表达如下

其中，每个用户表达分成两个部分，左边vu表示用户id映射的隐向量（user-based CF思想），右边是用户交互过的item集合的求和（item- based CF思想）。User和item的相似度还是用向量点击来表达。

这种融合方法可以看成早期的模型融合方法，在连续3年的Netflix百万美金推荐比赛中可是表现最好的模型。

---

Part2 Generic feature-based的方法

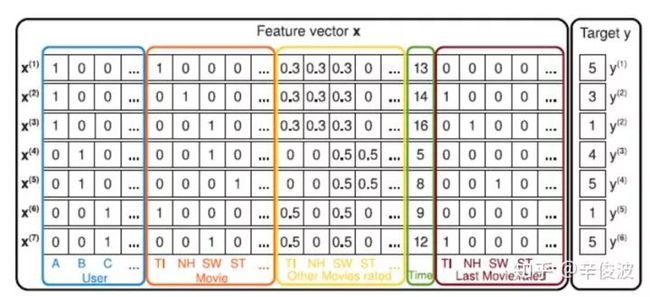
上述的方法中，无论是CF, MF, SVD, SVD++,还是FISM，都只是利用了user和item的交互信息（rating data），而对于大量的side information信息没有利用到。例如user本身的信息，如年龄，性别、职业；item本身的side information，如分类，描述，图文信息；以及context上下文信息，如位置，时间，天气等。因此，传统模型要讲的第二部分，是如何利用这些特征，去构造feature- based的model.

图2.3 特征体系三模块：用户信息、物品信息、交互信息

---

FM模型

首先要介绍的是大名鼎鼎的FM模型。FM模型可以看成由两部分组成，如图2.4所示，蓝色的LR线性模型，以及红色部分的二阶特征组合。对于每个输入特征，模型都需要学习一个低维的隐向量表达v，也就是在各种NN网络里所谓的embedding 表示。

图2.4 FM模型的稀疏one-hot特征输入

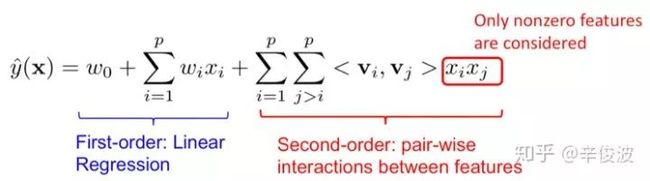
FM模型的数学表达如图2.5所示

图2.5 FM模型的数学表达分解

注意红色部分表示的是二阶特征的两两组合（特征自己和自己不做交叉），向量之间的交叉还是用向量内积表示。FM模型是feature- based模型的一个范式表达，接下来介绍的几个模型都可以看成是FM模型的特殊范例。

---

FM模型和MF关系

假如只使用userid和itemid，我们可以发现其实FM退化成加了bias的MF模型，如图2.6所示

图2.6 FM模型可以退化成带bias的MF模型

数学表达式如下：

---

FM模型和FISM关系

如果输入包含两个变量，1）用户交互过的item集合；2）itemid本身，那么，此时的FM又将退化成带bias的FISM模型，如图2.7所示，蓝色方框表示的是用户历史交互过的item(rated movies)，右边橙色方框表示的是itemid本身的one-hot特征

图2.7 FM模型可以退化成带bias的FISM模型

此时的FM模型数学表达如下：

同样道理，如果再加上userid的隐向量表达，那么FM模型将退化成SVD++模型。可见，MF, FISM, SVD++其实都是FM的特例。

---

Part3 总结

微观视角

上面介绍的模型都是通过打分预测来解决推荐系统的排序问题，这在很多时候一般都不是最优的，原因有如下几个方面：

（1）预测打分用的RMSE指标和实际的推荐系统排序指标的gap

预测打分用的RMSE拟合的是最小方差（带正则），而实际面临的是个排序问题

(2) 观察数据天然存在bias

用户一般倾向于给自己喜欢的item打分，而用户没有打分过的item未必就真的是不喜欢。针对推荐系统的排序问题，一般可以用pairwise 的ranking来替代RMSE

如上述公式所示，不直接拟合用户对item的单个打分，而是以pair的形式进行拟合；一般来说，用户打分高的item>用户打分低的item；用户用过交互的item>用户未交互过的item（不一定真的不喜欢）

---

宏观视角

推荐和搜索的本质其实都是匹配，前者匹配用户和物品；后者匹配query和doc。具体到匹配方法，分为传统模型和深度模型两大类，第二章讲的是传统模型，第三章和第四章讲的是深度模型。

对于传统模型，主要分为基于协同过滤的模型和基于特征的模型，两者最大的不同在于是否使用了side information。基于协同过滤的模型，如CF, MF, FISM, SVD++，只用到了用户-物品的交互信息，如userid， itemid， 以及用户交互过的item集合本身来表达。而基于特征的模型以FM为例，主要特点是除了用户-物品的交互之外，还引入了更多的side information。FM模型是很多其他模型的特例，如MF, SVD++，FISM等。

整理本篇综述主要基于原始slides，对其中的paper部分粗读部分精读，收获颇多，在全文用如何做好推荐match的思路，将各种方法尽可能串到一起，主要体现背后一致的思想指导。多有错漏，欢迎批评指出。

---

Part4 参考文献

(1)  https://www.  comp.nus.edu.sg/~xiangn  an/sigir18-deep.pdf

(2) Xiangnan He, Hanwang Zhang, Min-Yen Kan, and Tat-Seng Chua. Fast matrix factorization for online recommendation with implicit feedback. In SIGIR 2016.

(3) Yehuda Koren, and Robert Bell. Advances in collaborative filtering. Recommender systems handbook. Springer, Boston, MA, 2015. 77-118.

(4) Santosh Kabbur, Xia Ning, and George Karypis. Fism: factored item similarity models for top-n recommender systems. In KDD 2013.

(5) Yehuda Koren. Factorization meets the neighborhood: a multifaceted collaborative filtering model. In KDD 2018.

(6) Steffen Rendle. Factorization machines. In ICDM 2010.