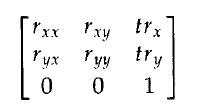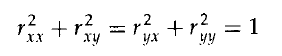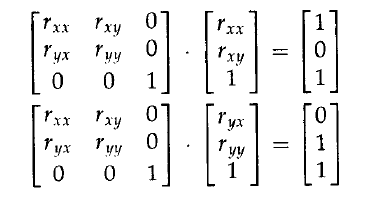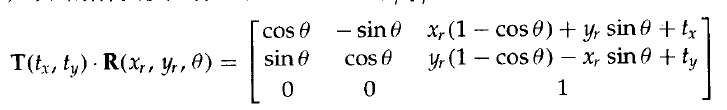- SerDes和GMSL介绍
槿盛
网络
SerDes(Serializer/Deserializer)SerDes,即串行器和解串器的缩写,是一种用于将并行数据转换为串行数据,以及将串行数据还原为并行数据的技术。这种技术广泛应用于各种高频率通信系统中,特别是在数据中心、汽车电子和消费电子设备中。SerDes的工作原理包括数据编码、调制和解调等多个步骤,这些步骤对于提高数据传输的效率和完整性至关重要。数据编码:在传输前,数据需要经过编码以
- vue中导入导出Excel
前端小白一枚
笔记vue导入导出Excel
以下仅个人做笔记使用:简单版导出Excel1、安装依赖:cnpminstall--savexlsxfile-savercnpmiscript-loader-S2、下载两个js文件:Blob.js和Export2Excel.js(放在最后面)3、添加导出按钮:导出数据4、添加导出事件:derive(){this.$http.post('admin/service_list',{pre_page:th
- 玩转传奇搭建,怎样用手里的云服务器搭建一款战神传奇手游技术教程,实现完全联网,实现多人同玩,10分钟学会架设游戏,云服务器或轻量云皆可搭建,快叫上朋友一起挂机砍怪吧!
qq_502428990
服务器游戏运维
这段时间不知怎么的,忽然有些怀念过往,想起十几年前和兄弟们网吧通宵砍传奇的场景,于时自己找了一些传奇代码,用云服务器搭建了一款传奇,怀念一下青春岁月!配置要求:最低2核4G,普通云服务器或轻量云皆可。系统要求:windows2008或者windows2012版64位。首先把服务器硬盘分出一个D盘来,云服务器默认没有D盘,需要从C盘分出一部分做D盘,当然你也可以购买,然后挂载上去。开始架设:第一步:
- MaxRetryError: HTTPConnectionPool(host=‘127.0.0.1‘, port=51379): Max retries exceeded with url: /ses
卢卡平头哥
Pythonpython
1.…暗示调用self.driver.close()方法失败引发MaxRetryError。2.有几件事:首先,根据讨论max-retries-exceeded异常令人困惑,回溯有些误导请求包装异常以方便用户。原始异常是显示消息的一部分请求永远不会重试(它为urllib3的HTTPConnectionPool设置retries=0)因此如果没有MaxRetryError和HTTPConnectio
- __init__.py 是个啥,为什么深受大厂程序员偏爱?
程序员CC_
Python入门学pythonPython零基础python人工智能开发语言
朋友们,今天我们来聊聊Python里一个低调却至关重要的文件——__init__.py。说实话,这玩意儿刚开始学Python时,很多人(包括当年的我)都是一脸懵:“这啥?删了会咋样?”有些人可能听说过它是“包的标志”,也有人觉得它“没啥大用,可以忽略”,更有甚者以为它“只是个装样子的文件”。今天,我们就来彻底搞清楚__init__.py到底是干啥的,以及它如何影响Python项目的结构和运行。️先
- 2022年 全国省、地级市、县行政区划及国界线shp格式
小王毕业啦
大数据人工智能数据分析数据挖掘大数据社科数据数据统计深度学习
最新全国省、地级市、县行政区划及国界线shp格式2022年.z.ziphttps://download.csdn.net/download/2401_84585615/89919937https://download.csdn.net/download/2401_84585615/89919937随着地理信息系统(GIS)技术的广泛应用,行政区划数据的获取和使用变得尤为重要。2022年全国省、地级
- 【vue导入导出Excel】vue简单实现导出和导入复杂表头excel表格功能【纯前端版本和配合后端版本】
2401_84433535
前端vue.jsexcel
### 配合后端的两个方法 因为上面的纯前端写法有一个问题,就是有分页的时候我们没法拿到数据。或者数据太大了我们下载实在是有点慢和卡。所以基本上工作中都是后端生成下载链接导出的。这里再分享两个方法。1,[a标签](https://bbs.csdn.net/topics/618166371)下载这种方法核心就是后端直接生成下载链接,前端只需要生成A标签然后下载就行了。较为常用的一个daochu(){
- jmeter中变量的作用范围_Jmeter 的变量类型和作用域
weixin_39789525
jmeter中变量的作用范围
Jmeter的有多种变量类型,有其各自的作用域。有时候不小心就会使它们之间相互冲突或者覆盖,本文梳理各种类型变量的生成方法、使用特点、作用范围。目录变量类型Jmeter中的变量分别有以下几种:UserDefinedVariablesUserParameters属性Properties运行中创建的变量我们分开单独研究各自的特点。UserDefinedVariables(UDV)UserDefined
- 打造安全认证系统:AWS Amplify与React集成
竹石文化传播有限公司
AWSAmplify用户认证React应用集成后端资源管理UI组件
背景简介在现代应用开发中,用户认证系统是保障安全和提供个性化体验的核心部分。本文将基于AWSAmplify的使用和配置,探讨如何在React应用程序中设置和集成一个全面的用户认证系统。设置认证系统所需的关键组件在为应用程序设置认证时,需要考虑以下几个重要组件:用户管理用户管理是指允许预定义用户列表访问系统,包括用户创建、阻止或删除等功能。角色管理角色管理涉及定义不同类型的用户角色,并将这些角色分配
- AWS中的 CloudFormation
等待的L先生
aws云计算
AWS中的CloudFormation1.CloudFormation是什么?AWSCloudFormation是亚马逊科技(AWS)提供的一项服务,允许用户通过模板来描述和配置,从而实现基础设施即代码(InfrastructureasCode,lac)。CloudFormation使用JSON或者YAML文件编写的模板来定义一组AWS资源的集合,称为“堆栈”,这些资源可以包括EC2实例,S3存储
- Android笔记(十五)ContentProvider源码浅析
jametang25
andorid
ContentProvider作为四大组件之一,由于业务上用到的地方不多,目前业务是系统界面,属于系统应用,最适合使用ContentProvider来进行少量数据存储,我们业务中涉及到的Settings.system和Settings.Secure等数据库,就是通过ContentProvider来封装、用ContentResolver来访问的//通过ContentResolver来访问Settin
- CloudFormation 实现 GitHub Actions OIDC 与 AWS ECR 的安全集成(支持多组织配置)
ivwdcwso
运维与云原生githubawsecrCI/CDOIDC流水线
、##引言:多组织场景下的安全挑战在企业环境中,经常需要为不同的GitHub组织(如开发组织dp和测试组织test)配置不同的访问权限。本文将详细介绍如何通过AWSCloudFormation模板实现灵活的OIDC集成,支持多GitHub组织的安全访问控制。第一部分:多组织架构设计安全认证流程(多组织场景)
- 设计的“第一性原理”:从Photoshop与Premiere Pro的AI革新谈起
最近有机会深入体验了一套来自英国ParvisSchoolofEconomicsandMusic的Adobe正版教育订阅,在把玩研究CreativeCloud全家桶的过程中,确实挖到了一些宝贝,感触颇深,忍不住想立刻和大家聊聊。先简单说下这套订阅给我的直观感受:它的FireflyAI积分是我见过最慷慨的,每周足足有1500点;授权设备数也达到了4台,可惜我囊中羞涩,并没有那么多设备去一一验证。最让我
- Python接口测试之接口关键字封装
测试老哥
python软件测试自动化测试职场和发展测试用例接口测试测试工具
点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快我们使用RF做UI自动化测试的时候,使用的是关键字驱动。同样,Python做接口自动化测试的时候,也可以使用关键字驱动。但是这里并不是叫关键字驱动,而是叫数据驱动。而接口测试的关键字是什么呢?我们数据驱动的载体是Excel,那么excel里存放的数据是接口测试用例数据,一个接口数据里有常量和变量。变量就是一些参数对应的值,而常量就是接口的
- 软件测试面试前该准备些什么?
AIZHINAN
面试软件测试面试软件测试面经简历包装面试技巧
在软件测试面试前,充分的准备可以显著提升你的信心和表现。以下是需要重点关注的准备方向,分为技术能力、项目经验、面试技巧和软技能四个部分:一、技术能力准备基础理论软件测试基本概念:测试类型(功能、性能、安全、兼容性等)、测试阶段(单元测试、集成测试、系统测试等)。经典面试题:黑盒vs白盒测试的区别?什么是边界值分析、等价类划分?Bug的生命周期是怎样的?如何设计测试用例?(举例:测试一个登录页面)测
- 主流接口测试框架对比
AIZHINAN
测试工具接口测试jmeter软件测试工程师测试框架
2025年最新jmeter接口测试完整版教程,零基础也能轻松掌握,用jmeter实现接口测试!JMeter接口测试、公司计划系统的开展接口自动化测试,需要我这边调研一下主流的接口测试框架给后端测试(主要测试接口)的同事介绍一下每个框架的特定和使用方式。后端同事根据他们接口的特点提出一下需求,看哪个框架更适合我们。需求1、接口编写方便。2、方便调试接口。3、支持数据初始化。4、生成测试报告。5、支持
- GitHub Actions 实现 AWS ECS 服务的多集群安全重启方案
ivwdcwso
运维与云原生githubaws安全DevOpsCI/CDgithubactions
引言在现代云原生架构中,容器化服务已成为主流。AmazonECS(ElasticContainerService)作为AWS的核心容器服务,管理着大量生产环境中的关键应用。服务重启是日常运维中的常见操作,无论是部署更新、修复问题还是刷新状态,都需要一种安全高效的机制。本文将介绍如何利用GitHubActions和AWSOIDC实现一个安全、灵活的多集群ECS服务重启方案。这个方案不仅简化了运维流程
- JMeter中变量如何使用?
测试者家园
智能化测试性能测试JMeterjmeter智能化测试性能测试软件测试质量效能软件开发和测试持续测试
在性能测试的世界中,ApacheJMeter是一把利器,凭借其强大的可扩展性与图形化操作界面,在工业界和开源社区中广受青睐。而“变量的使用”作为JMeter中提高测试灵活性、可维护性和复用性的关键技术点,却常常被初学者忽略或误用。本文将从变量的定义方式、作用域、典型应用场景到高级技巧全面展开剖析,并结合实际案例为读者提供具有启发性的思维视角。一、什么是变量?为什么JMeter离不开它?JMeter
- 红黑树与2-3树:插入、删除操作的时间复杂度与实现机制比较
一键难忘
红黑树数据结构
本文收录于专栏:算法之翼红黑树与2-3树:插入、删除操作的时间复杂度与实现机制比较红黑树(Red-BlackTree)和2-3树(2-3Tree)是两种广泛用于平衡二叉查找树的自平衡树结构。它们在插入、删除和查找操作中的性能都表现良好,并且可以确保树的高度是对数级别,从而保证了高效的操作时间。本文将对红黑树和2-3树进行深入的比较,并结合代码实例说明它们的实现和应用。1.数据结构简介1.1红黑树简
- 安装wordpress报错(完美解决)
光头程序员em
wordpress报错
#错误1#YourserverisrunningPHPversion7.2.1butWordPress6.7.1requiresatleast7.2.24.这是因为wordpress6.7.1需要7.2.24及以上版本,解决方法就是下载低版本wordpress或者升级高版本的php运行环境#错误2#不能选择数据库可以连接到数据库服务器(这说明您的用户名和密码正确),但是不能选择wordpress数
- 学习三维动画心得
2501_92205961
开发语言青少年编程
在大二学年的三维动画设计学习进程中,我围绕3dsMax和Blender两大核心软件展开深入钻研,并在此基础上探索技术应用与创新。不仅熟练掌握了基础操作,还深入到代码编写与复杂技术问题解决领域,逐步构建起系统的三维动画设计知识与技能体系,以下是详细的学习总结。一、3dsMax的深度学习与技术实践(一)高级建模与脚本优化在3dsMax的学习中,基础建模掌握后,我开始挑战高级建模技术。利用NURBS建模
- Python网安-zip文件暴力破解(仅供学习)
Whoisshutiao
python网安python开发语言网络安全
目录源码在这里需要的模块准备一个密码本和需要破解的ZIP文件一行一行地从密码文件中读取每个密码。核心部分注意,需要修改上段代码注释里的这段具有编码问题的代码:源码在这里https://github.com/Wist-fully/Attack/tree/cracker需要的模块fromtqdmimporttqdmimportzipfileimportpyzipper准备一个密码本和需要破解的ZIP文
- 【力扣hot100】python刷题笔记之哈希
Animato.
哈希算法leetcode笔记
1.两数之和(简单)题目描述:给定一个整数数组nums和一个整数目标值target,请你在该数组中找出和为目标值target的那两个整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。你可以按任意顺序返回答案。示例:解法一:暴力解法:双层循环(这里就不给代码了)解法二:哈希表(时间复杂度O(n))算法思路:(1)先创建一个空字典当做哈希表来存储已经遍历过的
- Qt实现tcp通信(QTcpServer和QTcpSocket的应用)详细教程
Qt实现tcp通信(QTcpServer和QTcpSocket的应用)详细教程服务端监听地址和端口ip可以是Ipv4Any,本机地址,也可以是固定的某个ip端口号则作为服务端绑定的端口,客户端连接服务端时需要连接到服务端绑定的端口,端口不对连接失败m_server=newQTcpServer(this);m_server->listen(QHostAddress::AnyIPv4,serverPo
- AI对话导出工具 (AI Chat Exporter)——支持 ChatGPT, Grok 和 Gemini 平台
ALGORITHM LOL
人工智能chatgpt
AI对话导出工具(AIChatExporter)轻松将AI对话导出为标准Markdown格式支持ChatGPT,Grok和Gemini平台相关代码已开源至Github欢迎Star✨功能特点多平台支持:同时支持ChatGPT,Grok和Gemini三大AI平台完整内容保留:精确导出所有对话内容,包括代码块、数学公式、链接和格式化文本标准Markdown格式:输出符合标准的Markdown格式,确保最
- AMHS工程项目中-MCS-STKC之间的office 测试场景的介绍
爱吃青菜的大力水手
半导体自动化AMHSMCS
工业自动化/半导体/面板制造等行业中常见的系统间接口预调试测试,通常称为Mockup测试、Office测试或FAT-Simulation测试。它的核心目标是在设备实际搬入工厂现场并连接真实物理设备之前,在办公室环境中验证上位系统(MCS)与下位系统(STOCKER控制器)之间的通信接口、协议逻辑和业务流程是否正常工作。以下是针对此场景的详细解读和关键点:核心目标:验证通信协议互通性:确保MCS发送
- 程序员思维
SHIZHONGYUO
思维语言应用程序软件编程
起因首先简单说一下,为什么我会想到这个话题。主要有这么几方面的原因。当我试图回过头去总结大学在计算机专业所学习的一些理论和知识的时候。发现,在学校里面学习的一些东西,走了两个极端。一个极端是偏向了细节。比如我们学习的那些《***程序设计》的课程。看这几门课的名称的我们能够很明显的看出,***是一个形容词定语,用来修饰主题“程序设计”。但是,你却非常意外的意识到《C++面向对象程序设计》和面向对象程
- 打造连贯性:如何通过过渡句提升论文的逻辑流畅性
学境思源AcademicIdeas
AI写作ChatGPT学境思源chatgpt人工智能
在学术写作中,逻辑连贯性是衡量论文质量的重要标准之一。即使论点扎实、数据详实,缺乏连贯性的论文仍可能让读者感到困惑。过渡句作为连接不同段落和章节的重要桥梁,能够有效地提升文章的逻辑流畅性,使内容更加易于理解。今天的内容我们将深入探讨过渡句的重要性,并提供实用技巧和示例,帮助写作者在论文中实现自然过渡,提升整体阅读体验。通过掌握这些方法,作者可以确保其研究成果得到更好的展示和认可。1.过渡句的重要性
- 生成式AI技术对未来知识生产模式的颠覆性影响:跨学科案例分析
德宿
人工智能
引言随着人工智能技术的迅猛发展,生成式AI作为一种革命性技术正在深刻地改变人类知识生产和学术研究的范式。生成式AI不仅能够创建原创内容,还能模拟人类思维过程,处理和生成大量数据,从而在各个学科领域展现出广阔的应用前景。本研究报告旨在深入探讨生成式AI技术对未来知识生产模式的颠覆性影响,通过对比传统学术研究与AI辅助研究的范式差异,并选取医学、法学、文学、经济学和艺术学等五个典型领域进行深度案例分析
- 广州华锐互动携手中石油:AR 巡检系统实现重大突破
广州华锐视点
ar
广州华锐互动在AR技术领域的卓越成就,通过一系列与知名企业、机构的成功合作案例得以充分彰显。其中,与中石油的合作项目堪称经典,展现了广州华锐互动运用AR技术解决实际难题、达成目标的强大实力。中石油作为能源行业的巨擘,在石油勘探、开采、运输和炼化等环节面临着诸多复杂的挑战。广州华锐互动与中石油携手,针对其油田设备巡检和员工培训等关键业务场景,开发了一套定制化的AR解决方案。在油田设备巡检方面,传统的
- 如何用ruby来写hadoop的mapreduce并生成jar包
wudixiaotie
mapreduce
ruby来写hadoop的mapreduce,我用的方法是rubydoop。怎么配置环境呢:
1.安装rvm:
不说了 网上有
2.安装ruby:
由于我以前是做ruby的,所以习惯性的先安装了ruby,起码调试起来比jruby快多了。
3.安装jruby:
rvm install jruby然后等待安
- java编程思想 -- 访问控制权限
百合不是茶
java访问控制权限单例模式
访问权限是java中一个比较中要的知识点,它规定者什么方法可以访问,什么不可以访问
一:包访问权限;
自定义包:
package com.wj.control;
//包
public class Demo {
//定义一个无参的方法
public void DemoPackage(){
System.out.println("调用
- [生物与医学]请审慎食用小龙虾
comsci
生物
现在的餐馆里面出售的小龙虾,有一些是在野外捕捉的,这些小龙虾身体里面可能带有某些病毒和细菌,人食用以后可能会导致一些疾病,严重的甚至会死亡.....
所以,参加聚餐的时候,最好不要点小龙虾...就吃养殖的猪肉,牛肉,羊肉和鱼,等动物蛋白质
- org.apache.jasper.JasperException: Unable to compile class for JSP:
商人shang
maven2.2jdk1.8
环境: jdk1.8 maven tomcat7-maven-plugin 2.0
原因: tomcat7-maven-plugin 2.0 不知吃 jdk 1.8,换成 tomcat7-maven-plugin 2.2就行,即
<plugin>
- 你的垃圾你处理掉了吗?GC
oloz
GC
前序:本人菜鸟,此文研究学习来自网络,各位牛牛多指教
1.垃圾收集算法的核心思想
Java语言建立了垃圾收集机制,用以跟踪正在使用的对象和发现并回收不再使用(引用)的对象。该机制可以有效防范动态内存分配中可能发生的两个危险:因内存垃圾过多而引发的内存耗尽,以及不恰当的内存释放所造成的内存非法引用。
垃圾收集算法的核心思想是:对虚拟机可用内存空间,即堆空间中的对象进行识别
- shiro 和 SESSSION
杨白白
shiro
shiro 在web项目里默认使用的是web容器提供的session,也就是说shiro使用的session是web容器产生的,并不是自己产生的,在用于非web环境时可用其他来源代替。在web工程启动的时候它就和容器绑定在了一起,这是通过web.xml里面的shiroFilter实现的。通过session.getSession()方法会在浏览器cokkice产生JESSIONID,当关闭浏览器,此
- 移动互联网终端 淘宝客如何实现盈利
小桔子
移動客戶端淘客淘寶App
2012年淘宝联盟平台为站长和淘宝客带来的分成收入突破30亿元,同比增长100%。而来自移动端的分成达1亿元,其中美丽说、蘑菇街、果库、口袋购物等App运营商分成近5000万元。 可以看出,虽然目前阶段PC端对于淘客而言仍旧是盈利的大头,但移动端已经呈现出爆发之势。而且这个势头将随着智能终端(手机,平板)的加速普及而更加迅猛
- wordpress小工具制作
aichenglong
wordpress小工具
wordpress 使用侧边栏的小工具,很方便调整页面结构
小工具的制作过程
1 在自己的主题文件中新建一个文件夹(如widget),在文件夹中创建一个php(AWP_posts-category.php)
小工具是一个类,想侧边栏一样,还得使用代码注册,他才可以再后台使用,基本的代码一层不变
<?php
class AWP_Post_Category extends WP_Wi
- JS微信分享
AILIKES
js
// 所有功能必须包含在 WeixinApi.ready 中进行
WeixinApi.ready(function(Api) {
// 微信分享的数据
var wxData = {
&nb
- 封装探讨
百合不是茶
JAVA面向对象 封装
//封装 属性 方法 将某些东西包装在一起,通过创建对象或使用静态的方法来调用,称为封装;封装其实就是有选择性地公开或隐藏某些信息,它解决了数据的安全性问题,增加代码的可读性和可维护性
在 Aname类中申明三个属性,将其封装在一个类中:通过对象来调用
例如 1:
//属性 将其设为私有
姓名 name 可以公开
- jquery radio/checkbox change事件不能触发的问题
bijian1013
JavaScriptjquery
我想让radio来控制当前我选择的是机动车还是特种车,如下所示:
<html>
<head>
<script src="http://ajax.googleapis.com/ajax/libs/jquery/1.7.1/jquery.min.js" type="text/javascript"><
- AngularJS中安全性措施
bijian1013
JavaScriptAngularJS安全性XSRFJSON漏洞
在使用web应用中,安全性是应该首要考虑的一个问题。AngularJS提供了一些辅助机制,用来防护来自两个常见攻击方向的网络攻击。
一.JSON漏洞
当使用一个GET请求获取JSON数组信息的时候(尤其是当这一信息非常敏感,
- [Maven学习笔记九]Maven发布web项目
bit1129
maven
基于Maven的web项目的标准项目结构
user-project
user-core
user-service
user-web
src
- 【Hive七】Hive用户自定义聚合函数(UDAF)
bit1129
hive
用户自定义聚合函数,用户提供的多个入参通过聚合计算(求和、求最大值、求最小值)得到一个聚合计算结果的函数。
问题:UDF也可以提供输入多个参数然后输出一个结果的运算,比如加法运算add(3,5),add这个UDF需要实现UDF的evaluate方法,那么UDF和UDAF的实质分别究竟是什么?
Double evaluate(Double a, Double b)
- 通过 nginx-lua 给 Nginx 增加 OAuth 支持
ronin47
前言:我们使用Nginx的Lua中间件建立了OAuth2认证和授权层。如果你也有此打算,阅读下面的文档,实现自动化并获得收益。SeatGeek 在过去几年中取得了发展,我们已经积累了不少针对各种任务的不同管理接口。我们通常为新的展示需求创建新模块,比如我们自己的博客、图表等。我们还定期开发内部工具来处理诸如部署、可视化操作及事件处理等事务。在处理这些事务中,我们使用了几个不同的接口来认证:
&n
- 利用tomcat-redis-session-manager做session同步时自定义类对象属性保存不上的解决方法
bsr1983
session
在利用tomcat-redis-session-manager做session同步时,遇到了在session保存一个自定义对象时,修改该对象中的某个属性,session未进行序列化,属性没有被存储到redis中。 在 tomcat-redis-session-manager的github上有如下说明: Session Change Tracking
As noted in the &qu
- 《代码大全》表驱动法-Table Driven Approach-1
bylijinnan
java算法
关于Table Driven Approach的一篇非常好的文章:
http://www.codeproject.com/Articles/42732/Table-driven-Approach
package com.ljn.base;
import java.util.Random;
public class TableDriven {
public
- Sybase封锁原理
chicony
Sybase
昨天在操作Sybase IQ12.7时意外操作造成了数据库表锁定,不能删除被锁定表数据也不能往其中写入数据。由于着急往该表抽入数据,因此立马着手解决该表的解锁问题。 无奈此前没有接触过Sybase IQ12.7这套数据库产品,加之当时已属于下班时间无法求助于支持人员支持,因此只有借助搜索引擎强大的
- java异常处理机制
CrazyMizzz
java
java异常关键字有以下几个,分别为 try catch final throw throws
他们的定义分别为
try: Opening exception-handling statement.
catch: Captures the exception.
finally: Runs its code before terminating
- hive 数据插入DML语法汇总
daizj
hiveDML数据插入
Hive的数据插入DML语法汇总1、Loading files into tables语法:1) LOAD DATA [LOCAL] INPATH 'filepath' [OVERWRITE] INTO TABLE tablename [PARTITION (partcol1=val1, partcol2=val2 ...)]解释:1)、上面命令执行环境为hive客户端环境下: hive>l
- 工厂设计模式
dcj3sjt126com
设计模式
使用设计模式是促进最佳实践和良好设计的好办法。设计模式可以提供针对常见的编程问题的灵活的解决方案。 工厂模式
工厂模式(Factory)允许你在代码执行时实例化对象。它之所以被称为工厂模式是因为它负责“生产”对象。工厂方法的参数是你要生成的对象对应的类名称。
Example #1 调用工厂方法(带参数)
<?phpclass Example{
- mysql字符串查找函数
dcj3sjt126com
mysql
FIND_IN_SET(str,strlist)
假如字符串str 在由N 子链组成的字符串列表strlist 中,则返回值的范围在1到 N 之间。一个字符串列表就是一个由一些被‘,’符号分开的自链组成的字符串。如果第一个参数是一个常数字符串,而第二个是type SET列,则 FIND_IN_SET() 函数被优化,使用比特计算。如果str不在strlist 或st
- jvm内存管理
easterfly
jvm
一、JVM堆内存的划分
分为年轻代和年老代。年轻代又分为三部分:一个eden,两个survivor。
工作过程是这样的:e区空间满了后,执行minor gc,存活下来的对象放入s0, 对s0仍会进行minor gc,存活下来的的对象放入s1中,对s1同样执行minor gc,依旧存活的对象就放入年老代中;
年老代满了之后会执行major gc,这个是stop the word模式,执行
- CentOS-6.3安装配置JDK-8
gengzg
centos
JAVA_HOME=/usr/java/jdk1.8.0_45
JRE_HOME=/usr/java/jdk1.8.0_45/jre
PATH=$PATH:$JAVA_HOME/bin:$JRE_HOME/bin
CLASSPATH=.:$JAVA_HOME/lib/dt.jar:$JAVA_HOME/lib/tools.jar:$JRE_HOME/lib
export JAVA_HOME
- 【转】关于web路径的获取方法
huangyc1210
Web路径
假定你的web application 名称为news,你在浏览器中输入请求路径: http://localhost:8080/news/main/list.jsp 则执行下面向行代码后打印出如下结果: 1、 System.out.println(request.getContextPath()); //可返回站点的根路径。也就是项
- php里获取第一个中文首字母并排序
远去的渡口
数据结构PHP
很久没来更新博客了,还是觉得工作需要多总结的好。今天来更新一个自己认为比较有成就的问题吧。 最近在做储值结算,需求里结算首页需要按门店的首字母A-Z排序。我的数据结构原本是这样的:
Array
(
[0] => Array
(
[sid] => 2885842
[recetcstoredpay] =&g
- java内部类
hm4123660
java内部类匿名内部类成员内部类方法内部类
在Java中,可以将一个类定义在另一个类里面或者一个方法里面,这样的类称为内部类。内部类仍然是一个独立的类,在编译之后内部类会被编译成独立的.class文件,但是前面冠以外部类的类名和$符号。内部类可以间接解决多继承问题,可以使用内部类继承一个类,外部类继承一个类,实现多继承。
&nb
- Caused by: java.lang.IncompatibleClassChangeError: class org.hibernate.cfg.Exten
zhb8015
maven pom.xml关于hibernate的配置和异常信息如下,查了好多资料,问题还是没有解决。只知道是包冲突,就是不知道是哪个包....遇到这个问题的分享下是怎么解决的。。
maven pom:
<dependency>
<groupId>org.hibernate</groupId>
<ar
- Spark 性能相关参数配置详解-任务调度篇
Stark_Summer
sparkcachecpu任务调度yarn
随着Spark的逐渐成熟完善, 越来越多的可配置参数被添加到Spark中来, 本文试图通过阐述这其中部分参数的工作原理和配置思路, 和大家一起探讨一下如何根据实际场合对Spark进行配置优化。
由于篇幅较长,所以在这里分篇组织,如果要看最新完整的网页版内容,可以戳这里:http://spark-config.readthedocs.org/,主要是便
- css3滤镜
wangkeheng
htmlcss
经常看到一些网站的底部有一些灰色的图标,鼠标移入的时候会变亮,开始以为是js操作src或者bg呢,搜索了一下,发现了一个更好的方法:通过css3的滤镜方法。
html代码:
<a href='' class='icon'><img src='utv.jpg' /></a>
css代码:
.icon{-webkit-filter: graysc