自动驾驶-用无损卡尔曼滤波算法定位

前边章节介绍了卡尔曼滤波的原理，并用扩展卡尔曼滤波实现匀速直线运动模型的车辆定位。从上章的介绍了解到，扩展卡尔曼滤波的方式要用到非线性的转移函数和对该函数求偏导得到的雅可比矩阵。如果转移函数比较复杂，那么求解雅可比矩阵计算量也很大，为了应对这种情况，无损卡尔曼滤波应运而生。

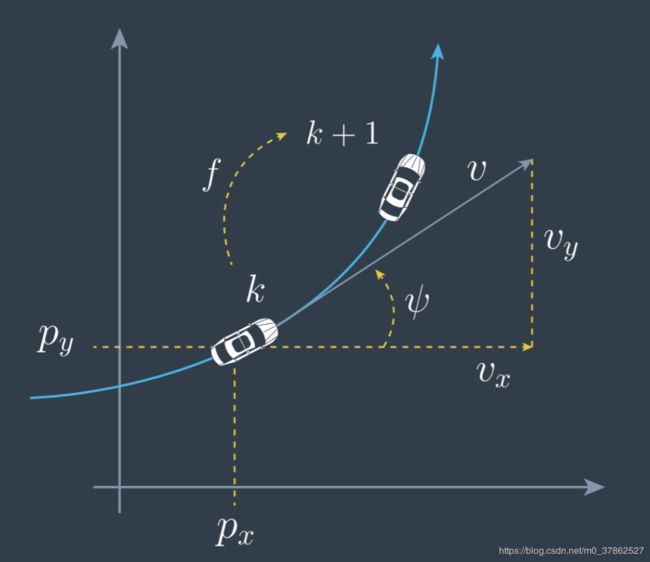
下图给出的是车辆转弯的模型，相比匀速直线运动，这一模型加入了向角$\psi$和航向角速度$\dot{\psi }$；为了使模型更接近实际情况，在计算状态向量时还考虑到加速度$a$和航向角加速度$\ddot{\psi }$对状态向量的影响。

状态方程：
$$\text{State}=x_{k+1}=x_k+\left[\begin{array}{c}\frac{v_k}{{\dot{\psi }}_k}(sin({\psi }_k+{\dot{\psi }}_k\Delta t)-sin({\psi }_k))\\ \frac{v_k}{{\dot{\psi }}_k}(-cos({\psi }_k+{\dot{\psi }}_k\Delta t)+cos({\psi }_k))\\ 0\\ {\dot{\psi }}_k\Delta t\\ 0\end{array}\right]+\left[\begin{array}{c}\frac{1}{2}(\Delta t{)}^{2}cos({\psi }_k){\nu }_{a,k}\\ \frac{1}{2}(\Delta t{)}^{2}sin({\psi }_k){\nu }_{a,k}\\ \Delta t\cdot {\nu }_{a,k}\\ \frac{1}{2}(\Delta t{)}^2{\nu }_{\ddot{\psi },k}\\ \Delta t\cdot {\nu }_{\ddot{\psi },k}\end{array}\right]$$

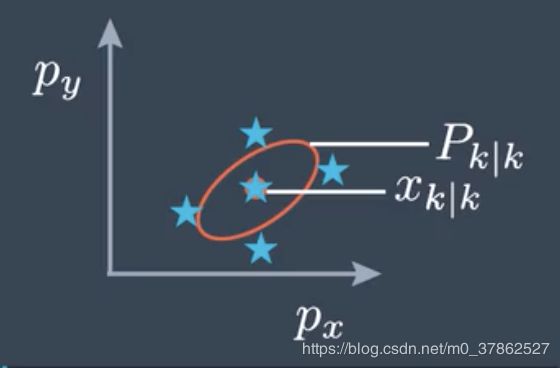
前面章节提到过，状态向量$x$可以当作其满足高斯分布的均值，协方差矩阵$P$就是其满足高斯分布的协方差。无损卡尔曼滤波利用这一分布特征，直接抽样多个点，一般将抽样点称为sigma点，在卡尔曼滤波预测阶段直接对所有抽样点进行预测得到预测sigma点，sigma点是满足某一高斯分布的采样点，实际想要的预测状态向量就是根据采样点得到一个均值，即状态向量的预测值，同时计算预测协方差；测量更新阶段再把预测sigma点映射到测量向量的域，暂且称其为测量sigma点，此时的测量sigma点是根据高斯分布采样出的若干点，同样的，此时想得到sigma点的均值，暂且称为测量预测向量，并计算协方差；最后就和普通卡尔曼滤波算法一样，得到一个新的满足高斯分布的状态向量的均值和方差。

无损滤波器的步骤可以概括为五步：

1. 生成sigma点
2. 预测sigma点
3. 计算预测均值和方差
4. 计算预测测量值
5. 更行状态

下面开始解释每一步的具体内容并给出源码实现。

生成sigma点

一般情况下，设状态向量包含$n_x$个变量，一般simg点的数量为2n_x+1$，用以下公式得到一个由$2n_x+1$个sigma点组成的向量，根据经验$\lambda$，这里$\lambda =3-n_x$，

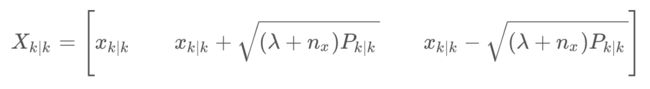
该公式的代码实现为：

 VectorXd x_aug = VectorXd(7);
 MatrixXd Xsig_aug = MatrixXd(n_aug_, 2 * n_aug_ + 1);
  
  x_aug.head(5) = x_;
  x_aug(5) = 0;
  x_aug(6) = 0;

  //create augmented covariance matrix
  P_aug.fill(0.0);
  P_aug.topLeftCorner(5,5) = P_;
  P_aug(5,5) = std_a_*std_a_;
  P_aug(6,6) = std_yawdd_*std_yawdd_;

  //create square root matrix
  MatrixXd L = P_aug.llt().matrixL();

  //create augmented sigma points
  Xsig_aug.col(0)  = x_aug;
  for (int i = 0; i< n_aug_; i++)
  {
    Xsig_aug.col(i+1)       = x_aug + sigma_spread_coef_ * L.col(i);
    Xsig_aug.col(i+1+n_aug_) = x_aug - sigma_spread_coef_ * L.col(i);
  }

因为考虑了加速度和航向角加速度，所以定义一个7维向量。

预测sigma点

生成sigma点后，使用第一个公式表示的状态转移方程计算每个sigma点的预测值，

  //predict sigma points
  for (int i = 0; i< 2*n_aug_+1; i++)
  {
    //extract values for better readability
    double p_x = Xsig_aug(0,i);
    double p_y = Xsig_aug(1,i);
    double v = Xsig_aug(2,i);
    double yaw = Xsig_aug(3,i);
    double yawd = Xsig_aug(4,i);
    double nu_a = Xsig_aug(5,i);
    double nu_yawdd = Xsig_aug(6,i);
    
    //create vector for weights
    weights_ = VectorXd(2*n_aug_+1);
 
    // set weights
    double weight_0 = lambda_/(lambda_+n_aug_);
    weights_(0) = weight_0;
    for (int i=1; i<2*n_aug_+1; i++) {  //2n+1 weights
    double weight = 0.5/(lambda_+n_aug_);
    weights_(i) = weight;
    }
   //avoid division by zero
    if (fabs(yawd) > 0.001) {
        px_p = p_x + v/yawd * ( sin (yaw + yawd*delta_t) - sin(yaw));
        py_p = p_y + v/yawd * ( cos(yaw) - cos(yaw+yawd*delta_t) );
    }
    else {
        px_p = p_x + v*delta_t*cos(yaw);
        py_p = p_y + v*delta_t*sin(yaw);
    }

    double v_p = v;
    double yaw_p = yaw + yawd*delta_t;
    double yawd_p = yawd;

    //add noise
    px_p = px_p + 0.5*nu_a*delta_t*delta_t * cos(yaw);
    py_p = py_p + 0.5*nu_a*delta_t*delta_t * sin(yaw);
    v_p = v_p + nu_a*delta_t;

    yaw_p = yaw_p + 0.5*nu_yawdd*delta_t*delta_t;
    yawd_p = yawd_p + nu_yawdd*delta_t;

    //write predicted sigma point into right column
    Xsig_pred_(0,i) = px_p;
    Xsig_pred_(1,i) = py_p;
    Xsig_pred_(2,i) = v_p;
    Xsig_pred_(3,i) = yaw_p;
    Xsig_pred_(4,i) = yawd_p;
  }

预测均值和方差

根据$2n_x+1$维的sigma预测值计算预测阶段的状态向量，注意计算状态向量的过程其实就是求每个特征值的均值，sigma点越靠近中心的位置准确度越高，应该给更高的权重，预测sigma点和预测状态向量的差值的协方差就是预测状态向量的方差，这一点也好理解，因为sigma 点等于均值加标准差，所以预测均值减sigma点就近似标准差。权重和预测状态向量的均值和方差用以下公式计算：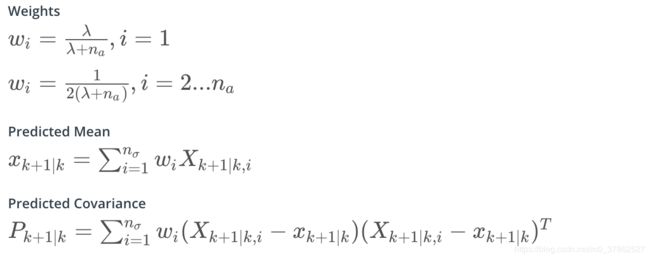

 //predicted state values
 double px_p, py_p;
   
 //predicted state mean
  x_.fill(0.0);
  for (int i = 0; i < 2 * n_aug_ + 1; i++) {  //iterate over sigma points
    x_ = x_+ weights_(i) * Xsig_pred_.col(i);
  }

  //predicted state covariance matrix
  P_.fill(0.0);
  for (int i = 0; i < 2 * n_aug_ + 1; i++) {  //iterate over sigma points
    // state difference
    VectorXd x_diff = Xsig_pred_.col(i) - x_;
    //angle normalization
    NormalizeAngle(x_diff(3));

    P_ = P_ + weights_(i) * x_diff * x_diff.transpose() ;

预测测量向量

这一步和卡尔曼滤波将预测值映射到测量向量域原理相似，对激光传感器，就用预测阶段sigma点的预测值的$p_x,p_y$加权平均计算预测测量向量，对雷达传感器，则是把预测阶段的sigma点的预测值转换为测量向量空间域的sigma点，再计算加权平均，然后将实际测量向量减去预测测量向量，其差值用来计算预测测量向量的协方差，另外，还要考虑设备误差$R$。按以下公式计算预测测量值的均值和方差：

以下为计算预测测量值的源码

  MatrixXd Zsig = MatrixXd(n_z_radar_, 2 * n_aug_ + 1);

  //create matrix for cross correlation Tc
  MatrixXd Tc = MatrixXd(n_x_, n_z_radar_);

  VectorXd z = VectorXd(n_z_radar_);
  z << meas_package.raw_measurements_[0],
        meas_package.raw_measurements_[1],
        meas_package.raw_measurements_[2];

  //transform sigma points into measurement space
  for (int i = 0; i < 2 * n_aug_ + 1; i++) {  //2n+1 simga points

    // extract values for better readibility
    double p_x = Xsig_pred_(0,i);
    double p_y = Xsig_pred_(1,i);
    double v  = Xsig_pred_(2,i);
    double yaw = Xsig_pred_(3,i);

    double v1 = cos(yaw)*v;
    double v2 = sin(yaw)*v;
    double eps = 0.00001;
    // measurement model

    Zsig(0,i) = sqrt(p_x*p_x + p_y*p_y);                   //r
    if ((p_y==p_x)&&(p_x)==0.0)
        Zsig(1,i) = 0.0;
    else
        Zsig(1,i) = atan2(p_y,p_x);                   //phi
    Zsig(2,i) = (p_x*v1 + p_y*v2 ) / max(eps,Zsig(0,i));   //r_dot
  }

  //mean predicted measurement
  VectorXd z_pred = VectorXd(n_z_radar_);
  z_pred.fill(0.0);
  for (int i=0; i < 2*n_aug_+1; i++) {
      z_pred = z_pred + weights_(i) * Zsig.col(i);
  }

  //measurement covariance matrix S
  MatrixXd S = MatrixXd(n_z_radar_,n_z_radar_);
  Tc.fill(0.0);

  S.fill(0.0);
  for (int i = 0; i < 2 * n_aug_ + 1; i++) {  //2n+1 simga points
    //residual
    VectorXd z_diff = Zsig.col(i) - z_pred;

    //angle normalization
    NormalizeAngle(z_diff(1));
    
    S = S + weights_(i) * z_diff * z_diff.transpose();
   
    // state difference
    VectorXd x_diff = Xsig_pred_.col(i) - x_;
  
    //angle normalization
    NormalizeAngle(x_diff(3));

    Tc = Tc + weights_(i) * x_diff * z_diff.transpose();

  }

  //add measurement noise covariance matrix
  S = S + R_radar_;

更新状态

最后一步就是更新状态，利用前面的结果计算$k$时刻状态向量的均值和方差，算法和卡尔曼滤波相同。

  //update state mean and covariance matrix
  x_ = x_ + K * z_diff;
  P_ = P_ - K*S*K.transpose();

以上就是本章的全部内容，完整代码请戳这里。