FVM in CFD 学习笔记_第9章_梯度计算
学习自F. Moukalled, L. Mangani, M. Darwish所著The Finite Volume Method in Computational Fluid Dynamics - An Advanced Introduction with OpenFOAM and Matlab
Chapter 9 Gradient Computation
FVM in CFD 学习笔记_第9章_梯度计算
在CFD的FVM的离散过程中,在单元形心和面形心处变量 ϕ \phi ϕ的梯度是常常要用到的物理量,那么如何由单元形心处的变量 ϕ \phi ϕ来获取单元形心和面形心处的变量 ϕ \phi ϕ的梯度 ∇ ϕ \nabla \phi ∇ϕ呢?本节便讲讲FVM in CFD中梯度的计算方法。
1 笛卡尔网格上梯度的计算
由于笛卡尔网格横平竖直,有很好的正交特性,所以梯度的计算变得十分简单快捷了,对于1维问题,且均匀网格,则面 e e e上的变量梯度可直接得出:

( ∂ ϕ ∂ x ) e = ϕ E − ϕ C x E − x C = ϕ E − ϕ C δ x e \left(\frac{\partial\phi}{\partial x}\right)_e=\frac{\phi_E-\phi_C}{x_E-x_C}=\frac{\phi_E-\phi_C}{\delta x_e} (∂x∂ϕ)e=xE−xCϕE−ϕC=δxeϕE−ϕC
单元形心 C C C处的变量梯度也可得出
( ∂ ϕ ∂ x ) C = ϕ e − ϕ w x e − x w = ϕ E + ϕ C 2 − ϕ C + ϕ W 2 Δ x C = ϕ E − ϕ W 2 Δ x C \left(\frac{\partial\phi}{\partial x}\right)_C=\frac{\phi_e-\phi_w}{x_e-x_w}=\frac{\displaystyle \frac{\phi_E+\phi_C}{2}-\frac{\phi_C+\phi_W}{2}}{\Delta x_C}=\frac{\phi_E-\phi_W}{2 \Delta x_C} (∂x∂ϕ)C=xe−xwϕe−ϕw=ΔxC2ϕE+ϕC−2ϕC+ϕW=2ΔxCϕE−ϕW
这个常叫做“中心差分”,对于2维情况,与此类似,可得
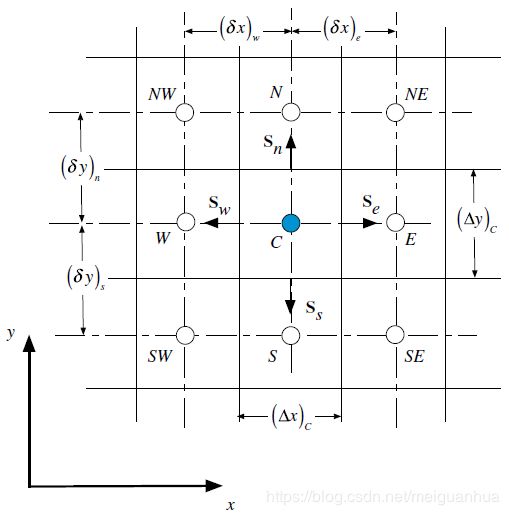
( ∂ ϕ ∂ x ) C = ϕ E − ϕ W x E − x W , ( ∂ ϕ ∂ y ) C = ϕ N − ϕ S x N − x S \left(\frac{\partial\phi}{\partial x}\right)_C=\frac{\phi_E-\phi_W}{x_E-x_W},\quad \left(\frac{\partial\phi}{\partial y}\right)_C=\frac{\phi_N-\phi_S}{x_N-x_S} (∂x∂ϕ)C=xE−xWϕE−ϕW,(∂y∂ϕ)C=xN−xSϕN−ϕS
当处理非正交网格或非结构网格时,情况就复杂得多了,这就需要用到更加通用方法,即Green-Gauss梯度法和最小二乘梯度法等。
2 Green-Gauss Gradient(格林-高斯梯度)
这是计算梯度方法中应用最广的一个,即,单元形心处变量的梯度可以由面形心处的变量值与面积矢量复合后相加和除以单元体积来获取,用到的数学定理是Green-Gauss或梯度定理,即
∫ V ∇ ϕ d V = ∮ ∂ V ϕ d S ⃗ ⇒ ∇ ϕ ‾ V = ∮ ∂ V ϕ d S ⃗ ⇒ ∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f S ⃗ f \int_V\nabla\phi dV=\oint_{\partial V}\phi d\vec S \Rightarrow \overline{\nabla\phi} V =\oint_{\partial V}\phi d\vec S \Rightarrow \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_f \vec S_f ∫V∇ϕdV=∮∂VϕdS⇒∇ϕV=∮∂VϕdS⇒∇ϕC=VC1f−nb(C)∑ϕfSf
即
∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f S ⃗ f \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_f \vec S_f ∇ϕC=VC1f−nb(C)∑ϕfSf
其中 V C V_C VC为单元体积, f f f代表单元的某个面,而 S ⃗ f \vec S_f Sf为该面的面积矢量,面形心的变量值 ϕ f \phi_f ϕf是未知的,仍旧需要计算出来,不然上面这个公式是用不了的。 ϕ f \phi_f ϕf的计算方法有两种,一是用紧致框架(compact stencil)由面左右单元(所属单元和邻居单元,即面两侧单元)形心值来计算,二是用扩展框架(extended stencil)先用面的角点周围单元上的值来得到面的角点值,然后再由角点值来平均得到面形心的值。
方法1:紧致框架
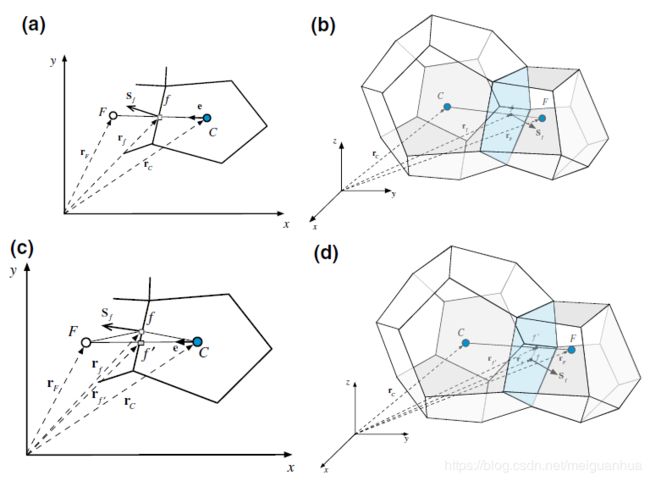
对于上图(a)和(b)所示的2维和3维情况,一种最简单的方法是直接由面两侧单元形心值平均来获得面上变量的值,即
ϕ f = g C ϕ C + ( 1 − g C ) ϕ F \phi_f=g_C\phi_C+(1-g_C)\phi_F ϕf=gCϕC+(1−gC)ϕF
其中 g C g_C gC为几何权重系数,等于
g C = ∣ ∣ r ⃗ F − r ⃗ f ∣ ∣ ∣ ∣ r ⃗ F − r ⃗ C ∣ ∣ = d F f d F C g_C=\frac{||\vec r_F-\vec r_f||}{||\vec r_F-\vec r_C||}=\frac{d_{Ff}}{d_{FC}} gC=∣∣rF−rC∣∣∣∣rF−rf∣∣=dFCdFf
其中 r ⃗ \vec r r为距离矢量,而 d d d为两点之间的距离值,若该面恰好位于两单元中心的中间位置,则有
ϕ f = ϕ C + ϕ F 2 \phi_f=\frac{\phi_C+\phi_F}{2} ϕf=2ϕC+ϕF
这个方法非常简便易行,然而遗憾的是,只有当线段 C F CF CF和面 S ⃗ f \vec S_f Sf的交点与面 S ⃗ f \vec S_f Sf的中心重合时(即上图(a)(b)情况),该方法才能保证2阶精度,而大多数情况下,直接由上式算得的梯度精度是没法保证的。
然而,对于通常的非正交网格和非结构网格来说,是没有办法来保证这个条件的,比如上图中的(c)(d)情况,网格的偏斜(非正交,skewness(non-conjunctionality))使得线段 C F CF CF和面 S ⃗ f \vec S_f Sf交点为 f ′ f' f′,与面形心 f f f是不重合的。此时,需要把插值得到的 ϕ f ′ \phi_{f'} ϕf′修正以得到 ϕ f \phi_f ϕf,修正方程为
ϕ f = ϕ f ′ + c o r r e c t i o n = ϕ f ′ + ( ∇ ϕ ) f ′ ⋅ ( r ⃗ f − r ⃗ f ′ ) \phi_f=\phi_{f'}+correction=\phi_{f'}+(\nabla\phi)_{f'}\cdot(\vec r_f-\vec r_{f'}) ϕf=ϕf′+correction=ϕf′+(∇ϕ)f′⋅(rf−rf′)
即,用梯度 ( ∇ ϕ ) f ′ (\nabla\phi)_{f'} (∇ϕ)f′来修正,修正也可以展开为如下形式:
ϕ f = g C { ϕ C + ( ∇ ϕ ) C ⋅ ( r ⃗ f − r ⃗ C ) } + ( 1 − g C ) { ϕ F + ( ∇ ϕ ) F ⋅ ( r ⃗ f − r ⃗ F ) } = ϕ f ′ + g C ( ∇ ϕ ) C ⋅ ( r ⃗ f − r ⃗ C ) + ( 1 − g C ) ( ∇ ϕ ) F ⋅ ( r ⃗ f − r ⃗ F ) \phi_f=g_C\{\phi_C+(\nabla\phi)_C\cdot(\vec r_f-\vec r_C)\}+(1-g_C)\{ \phi_F+(\nabla\phi)_F\cdot(\vec r_f-\vec r_F) \}\\ \quad \\ =\phi_{f'}+g_C(\nabla\phi)_C\cdot(\vec r_f-\vec r_C)+(1-g_C)(\nabla\phi)_F\cdot(\vec r_f-\vec r_F) ϕf=gC{ϕC+(∇ϕ)C⋅(rf−rC)}+(1−gC){ϕF+(∇ϕ)F⋅(rf−rF)}=ϕf′+gC(∇ϕ)C⋅(rf−rC)+(1−gC)(∇ϕ)F⋅(rf−rF)
即, { ϕ C + ( ∇ ϕ ) C ⋅ ( r ⃗ f − r ⃗ C ) } \{\phi_C+(\nabla\phi)_C\cdot(\vec r_f-\vec r_C)\} {ϕC+(∇ϕ)C⋅(rf−rC)}是把 C C C处的值修正到 f f f处,而 { ϕ F + ( ∇ ϕ ) F ⋅ ( r ⃗ f − r ⃗ F ) } \{ \phi_F+(\nabla\phi)_F\cdot(\vec r_f-\vec r_F) \} {ϕF+(∇ϕ)F⋅(rf−rF)}是把 F F F处的值修正到 f f f处,然后再做加权插值处理,就得到了 ϕ f \phi_f ϕf。
不难发现, ϕ f \phi_f ϕf的修正计算要用到 ( ∇ ϕ ) C (\nabla\phi)_C (∇ϕ)C和 ( ∇ ϕ ) F (\nabla\phi)_F (∇ϕ)F,而 ( ∇ ϕ ) C (\nabla\phi)_C (∇ϕ)C和 ( ∇ ϕ ) F (\nabla\phi)_F (∇ϕ)F则是用 ϕ f \phi_f ϕf算得的,也就是说,这里 ϕ f \phi_f ϕf的计算是不能一蹴而就的,而是一个迭代计算的过程,但是过多的迭代反而会造成解的振荡,一般做两次迭代就好了。
另外, g C g_C gC是与点 f ′ f' f′的位置密切相关的,有三种选择方式:
选择1
点 f ′ f' f′就选择在线段 C F CF CF和面 S ⃗ f \vec S_f Sf的交点处,以 n ⃗ \vec n n代表面积单位矢量,即, n ⃗ = S ⃗ f / ∣ ∣ S ⃗ f ∣ ∣ \vec n=\vec S_f/||\vec S_f|| n=Sf/∣∣Sf∣∣,以 e ⃗ \vec e e代表沿着 C F CF CF的单位矢量,即 e ⃗ = C F → / ∣ ∣ C F → ∣ ∣ \vec e=\overrightarrow{CF}/||\overrightarrow{CF}|| e=CF/∣∣CF∣∣,则 f ′ f' f′的位置可由几何关系算出,为
r ⃗ f ′ = ( r ⃗ f − r ⃗ C ) ⋅ n ⃗ e ⃗ ⋅ n ⃗ e ⃗ + r ⃗ C = r ⃗ f ⋅ n ⃗ e ⃗ ⋅ n ⃗ e ⃗ \vec r_{f'}=\frac{(\vec r_f - \vec r_C) \cdot \vec n}{\vec e \cdot \vec n}\vec e+\vec r_C=\frac{\vec r_f \cdot \vec n}{\vec e \cdot \vec n}\vec e rf′=e⋅n(rf−rC)⋅ne+rC=e⋅nrf⋅ne
其中, ( r ⃗ f − r ⃗ C ) ⋅ n ⃗ (\vec r_f - \vec r_C) \cdot \vec n (rf−rC)⋅n为点 C C C到面 S ⃗ f \vec S_f Sf的垂直距离向量,分母 e ⃗ ⋅ n ⃗ \vec e \cdot \vec n e⋅n为该垂直向量与 C F → \overrightarrow{CF} CF夹角的余弦值 c o s θ cos\theta cosθ,于是两者相除便得到了 C C C到 f ′ f' f′的向量 C f ′ → \overrightarrow{Cf'} Cf′,再与 r ⃗ C \vec r_C rC相加便是点 f ′ f' f′的位置矢量。
得到 f ′ f' f′的位置后,可以直接算出 g C g_C gC的值
g C = ∣ ∣ r ⃗ F − r ⃗ f ′ ∣ ∣ ∣ ∣ r ⃗ F − r ⃗ C ∣ ∣ = d F f ′ d F C g_C=\frac{||\vec r_F - \vec r_{f'}||}{||\vec r_F - \vec r_{C}||}=\frac{d_{Ff'}}{d_{FC}} gC=∣∣rF−rC∣∣∣∣rF−rf′∣∣=dFCdFf′
计算流程如下:
- 计算 ϕ f ′ \phi_{f'} ϕf′使用 ϕ f ′ = g C ϕ C + ( 1 − g C ) ϕ F \phi_{f'}=g_C\phi_C+(1-g_C)\phi_F ϕf′=gCϕC+(1−gC)ϕF
- 计算 ∇ ϕ C \nabla\phi_C ∇ϕC使用 ∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f ′ S ⃗ f \displaystyle \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_{f'} \vec S_f ∇ϕC=VC1f−nb(C)∑ϕf′Sf
接下来用下面步骤来修正梯度场 - 更新 ϕ f \phi_{f} ϕf使用 ϕ f = ϕ f ′ + g C ( ∇ ϕ ) C ⋅ ( r ⃗ f − r ⃗ C ) + ( 1 − g C ) ( ∇ ϕ ) F ⋅ ( r ⃗ f − r ⃗ F ) \phi_f=\phi_{f'}+g_C(\nabla\phi)_C\cdot(\vec r_f-\vec r_C)+(1-g_C)(\nabla\phi)_F\cdot(\vec r_f-\vec r_F) ϕf=ϕf′+gC(∇ϕ)C⋅(rf−rC)+(1−gC)(∇ϕ)F⋅(rf−rF)
- 计算 ∇ ϕ C \nabla\phi_C ∇ϕC使用 ∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f S ⃗ f \displaystyle \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_{f} \vec S_f ∇ϕC=VC1f−nb(C)∑ϕfSf
- 返回步骤3再迭代一次。
选择2

点 f ′ f' f′就选择在线段 C F CF CF的中点,相当于 g C = 0.5 g_C=0.5 gC=0.5,这就使得计算简单多了,其计算流程如下:
- 计算 ϕ f ′ \phi_{f'} ϕf′使用 ϕ f ′ = ϕ C + ϕ F 2 \displaystyle \phi_{f'}=\frac{\phi_C+\phi_F}{2} ϕf′=2ϕC+ϕF
- 计算 ∇ ϕ C \nabla\phi_C ∇ϕC使用 ∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f ′ S ⃗ f \displaystyle \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_{f'} \vec S_f ∇ϕC=VC1f−nb(C)∑ϕf′Sf
接下来用下面步骤来修正梯度场 - 更新 ϕ f \phi_{f} ϕf使用 ϕ f = ϕ f ′ + ( ∇ ϕ ) C + ( ∇ ϕ ) F 2 ⋅ ( r ⃗ f − r ⃗ C + r ⃗ F 2 ) \displaystyle \phi_f=\phi_{f'}+\frac{(\nabla\phi)_C+(\nabla\phi)_F}{2}\cdot\left(\vec r_f-\frac{\vec r_C+\vec r_F}{2}\right) ϕf=ϕf′+2(∇ϕ)C+(∇ϕ)F⋅(rf−2rC+rF)
- 计算 ∇ ϕ C \nabla\phi_C ∇ϕC使用 ∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f S ⃗ f \displaystyle \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_{f} \vec S_f ∇ϕC=VC1f−nb(C)∑ϕfSf
- 返回步骤3再迭代一次。
选择3

点 f ′ f' f′的位置选择要保证距离 f f ′ ff' ff′是最短的,即, f f ′ ff' ff′是垂直于 C F CF CF的,这使得第1步迭代计算变得更加准确。 f ′ f' f′的位置计算很简单,直接把向量 C f → \overrightarrow {Cf} Cf投影到 C F → \overrightarrow {CF} CF上就妥了,即
r ⃗ f ′ = r ⃗ C + r ⃗ C f ⋅ r ⃗ C F r ⃗ C F ⋅ r ⃗ C F ( r ⃗ F − r ⃗ C ) \vec r_{f'}=\vec r_C+\frac{\vec r_{Cf} \cdot \vec r_{CF}}{\vec r_{CF} \cdot \vec r_{CF}}(\vec r_F-\vec r_C) rf′=rC+rCF⋅rCFrCf⋅rCF(rF−rC)
其计算流程如下:
- 计算 r ⃗ f ′ \vec r_{f'} rf′使用 r ⃗ f ′ = r ⃗ C + r ⃗ C f ⋅ r ⃗ C F r ⃗ C F ⋅ r ⃗ C F ( r ⃗ F − r ⃗ C ) \displaystyle\vec r_{f'}=\vec r_C+\frac{\vec r_{Cf} \cdot \vec r_{CF}}{\vec r_{CF} \cdot \vec r_{CF}}(\vec r_F-\vec r_C) rf′=rC+rCF⋅rCFrCf⋅rCF(rF−rC)
- 计算 g C g_C gC使用 g C = ∣ ∣ r ⃗ F − r ⃗ f ′ ∣ ∣ ∣ ∣ r ⃗ F − r ⃗ C ∣ ∣ \displaystyle g_C=\frac{||\vec r_F - \vec r_{f'}||}{||\vec r_F - \vec r_C||} gC=∣∣rF−rC∣∣∣∣rF−rf′∣∣
- 计算 ϕ f ′ \phi_{f'} ϕf′使用 ϕ f ′ = g C ϕ C + ( 1 − g C ) ϕ F \phi_{f'}=g_C\phi_C+(1-g_C)\phi_F ϕf′=gCϕC+(1−gC)ϕF
- 计算 ∇ ϕ C \nabla\phi_C ∇ϕC使用 ∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f ′ S ⃗ f \displaystyle \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_{f'} \vec S_f ∇ϕC=VC1f−nb(C)∑ϕf′Sf
接下来用下面步骤来修正梯度场 - 计算 ∇ ϕ f ′ \nabla\phi_{f'} ∇ϕf′使用 ∇ ϕ f ′ = g C ∇ ϕ C + ( 1 − g C ) ∇ ϕ F \nabla\phi_{f'}=g_C\nabla\phi_C+(1-g_C)\nabla\phi_F ∇ϕf′=gC∇ϕC+(1−gC)∇ϕF
- 更新 ϕ f \phi_{f} ϕf使用 ϕ f = ϕ f ′ + ∇ ϕ f ′ ⋅ ( r ⃗ f − r ⃗ f ′ ) \phi_f=\phi_{f'}+\nabla\phi_{f'}\cdot(\vec r_f-\vec r_{f'}) ϕf=ϕf′+∇ϕf′⋅(rf−rf′)
- 计算 ∇ ϕ C \nabla\phi_C ∇ϕC使用 ∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f S ⃗ f \displaystyle \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_{f} \vec S_f ∇ϕC=VC1f−nb(C)∑ϕfSf
- 返回步骤5再迭代一次。
例1
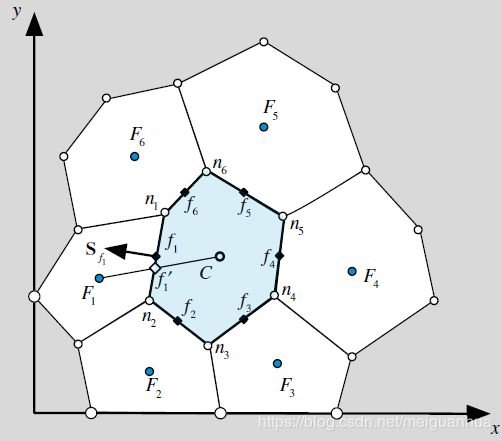
上图所示网格,单元形心 C C C与其邻近单元形心 F 1 F_1 F1到 F 6 F_6 F6的坐标为
C ( 13 , 11 ) , F 1 ( 4.5 , 9.5 ) , F 2 ( 8 , 3 ) , F 3 ( 17 , 3.5 ) , F 4 ( 22 , 10 ) , F 5 ( 16 , 20 ) , F 6 ( 7 , 18 ) C(13, 11), \quad F_1(4.5,9.5), \quad F_2(8,3), \quad F_3(17,3.5), \quad F_4(22,10), \quad F_5(16,20), \quad F_6(7,18) C(13,11),F1(4.5,9.5),F2(8,3),F3(17,3.5),F4(22,10),F5(16,20),F6(7,18)
角点 n 1 n_1 n1到 n 2 n_2 n2的坐标为
n 1 ( 9 , 14 ) , n 2 ( 8 , 8 ) , n 3 ( 12 , 5 ) , n 4 ( 17 , 9 ) , n 5 ( 17.5 , 14 ) , n 6 ( 12 , 17 ) n_1(9,14), \quad n_2(8,8), \quad n_3(12,5), \quad n_4(17,9), \quad n_5(17.5,14), \quad n_6(12,17) n1(9,14),n2(8,8),n3(12,5),n4(17,9),n5(17.5,14),n6(12,17)
变量 ϕ \phi ϕ在单元形心的值为
ϕ C = 167 , ϕ F 1 = 56.75 , ϕ F 2 = 35 , ϕ F 3 = 80 , ϕ F 4 = 252 , ϕ F 5 = 356 , ϕ F 6 = 151 \phi_C=167, \quad \phi_{F_1}=56.75, \quad \phi_{F_2}=35, \quad \phi_{F_3}=80, \quad \phi_{F_4}=252, \quad \phi_{F_5}=356, \quad\phi_{F_6}=151 ϕC=167,ϕF1=56.75,ϕF2=35,ϕF3=80,ϕF4=252,ϕF5=356,ϕF6=151
C单元的邻近单元形心处变量 ϕ \phi ϕ的梯度值 ∇ ϕ \nabla\phi ∇ϕ为
∇ ϕ F 1 = 10.5 i + 5.5 j , ∇ ϕ F 2 = 4 i + 9 j , ∇ ϕ F 3 = 4.5 i + 18 j , ∇ ϕ F 4 = 11 i + 23 j , ∇ ϕ F 5 = 21 i + 17 j , ∇ ϕ F 6 = 19 i + 8 j \nabla\phi_{F_1}=10.5\bold i+5.5 \bold j ,\quad \nabla\phi_{F_2}=4\bold i+9 \bold j, \quad \nabla\phi_{F_3}=4.5\bold i+18 \bold j, \\ \nabla\phi_{F_4}=11 \bold i+23 \bold j, \quad \nabla\phi_{F_5}=21 \bold i+17 \bold j, \quad \nabla\phi_{F_6}=19\bold i+8 \bold j ∇ϕF1=10.5i+5.5j,∇ϕF2=4i+9j,∇ϕF3=4.5i+18j,∇ϕF4=11i+23j,∇ϕF5=21i+17j,∇ϕF6=19i+8j
单元C的体积
V C = 76 V_C=76 VC=76
求解单元C形心处的梯度值 ∇ ϕ C \nabla\phi_C ∇ϕC,使用如下方法:
a. Green-Gauss方法,不含修正
b. Green-Gauss方法,含skewness correction, f ′ f' f′选择为线段CF的中点
解法a. Green-Gauss方法求解 ∇ ϕ C \nabla\phi_C ∇ϕC,不含修正
计算面形心(2维情况下就是面中心)坐标值
x f 1 = ( x n 1 + x n 2 ) / 2 = ( 9 + 8 ) / 2 = 8.5 y f 1 = ( y n 1 + y n 2 ) / 2 = ( 14 + 8 ) / 2 = 11 x_{f_1}=(x_{n_1}+x_{n_2})/2=(9+8)/2=8.5 \\ y_{f_1}=(y_{n_1}+y_{n_2})/2=(14+8)/2=11 xf1=(xn1+xn2)/2=(9+8)/2=8.5yf1=(yn1+yn2)/2=(14+8)/2=11
即
f 1 ( 8.5 , 11 ) f_1(8.5, 11) f1(8.5,11)
同样方法算得单元C的其余面的形心坐标
f 2 ( 10 , 6.5 ) , f 3 ( 14.5 , 7 ) , f 4 ( 17.25 , 11.5 ) , f 5 ( 14.75 , 15.5 ) , f 6 ( 10.5 , 15.5 ) f_2(10, 6.5), \quad f_3(14.5, 7), \quad f_4(17.25, 11.5), \quad f_5(14.75, 15.5), \quad f_6(10.5,15.5) f2(10,6.5),f3(14.5,7),f4(17.25,11.5),f5(14.75,15.5),f6(10.5,15.5)
计算面积矢量 S ⃗ f 1 \vec S_{f_1} Sf1
S ⃗ f 1 = Δ y i − Δ x j = ( y n 2 − y n 1 ) i − ( x n 2 − x n 1 ) j = ( 8 − 14 ) i − ( 8 − 9 ) j = − 6 i + j \vec S_{f_1}=\Delta y\bold i - \Delta x\bold j=(y_{n_2}-y_{n_1})\bold i - (x_{n_2}-x_{n_1}) \bold j \\ =(8-14)\bold i - (8-9) \bold j=-6\bold i + \bold j Sf1=Δyi−Δxj=(yn2−yn1)i−(xn2−xn1)j=(8−14)i−(8−9)j=−6i+j
同样方法算得其余面的面积矢量
S ⃗ f 2 = − 3 i − 4 j S ⃗ f 3 = 4 i − 5 j S ⃗ f 4 = 5 i − 0.5 j S ⃗ f 5 = 3 i + 5.5 j S ⃗ f 6 = − 3 i + 3 j \vec S_{f_2}=-3\bold i -4 \bold j \quad \vec S_{f_3}=4\bold i -5 \bold j \quad \vec S_{f_4}=5\bold i -0.5 \bold j \quad \vec S_{f_5}=3\bold i +5.5 \bold j \quad \vec S_{f_6}=-3\bold i +3 \bold j Sf2=−3i−4jSf3=4i−5jSf4=5i−0.5jSf5=3i+5.5jSf6=−3i+3j
计算插值系数 g C 1 g_{C_1} gC1
g C 1 = F 1 f 1 F 1 f 1 + C f 1 F 1 f 1 = ( 4.5 − 8.5 ) 2 + ( 9.5 − 11 ) 2 = 4.272 C f 1 = ( 13 − 8.5 ) 2 + ( 11 − 11 ) 2 = 4.5 g_{C_1}=\frac{F_1 f_1}{F_1 f_1+Cf_1} \\ \quad \\ F_1 f_1=\sqrt{(4.5-8.5)^2+(9.5-11)^2}=4.272 \\ \quad \\ Cf_1=\sqrt{(13-8.5)^2+(11-11)^2}=4.5 gC1=F1f1+Cf1F1f1F1f1=(4.5−8.5)2+(9.5−11)2=4.272Cf1=(13−8.5)2+(11−11)2=4.5
算得
g C 1 = 0.487 g_{C_1}=0.487 gC1=0.487
同样,算得其它面的插值系数
g C 2 = 0.427 , g C 3 = 0.502 , g C 4 = 0.538 , g C 5 = 0.492 , g C 6 = 0.455 g_{C_2}=0.427, \quad g_{C_3}=0.502, \quad g_{C_4}=0.538, \quad g_{C_5}=0.492, \quad g_{C_6}=0.455 gC2=0.427,gC3=0.502,gC4=0.538,gC5=0.492,gC6=0.455
计算面形心的变量值 ϕ f \phi_f ϕf
ϕ f 1 = g C 1 ϕ C + ( 1 − g C 1 ) ϕ F 1 = 0.487 ∗ 167 + ( 1 − 0.487 ) ∗ 56.75 = 110.442 \phi_{f_1}=g_{C_1}\phi_C+(1-g_{C_1})\phi_{F_1}=0.487*167+(1-0.487)*56.75=110.442 ϕf1=gC1ϕC+(1−gC1)ϕF1=0.487∗167+(1−0.487)∗56.75=110.442
同样算得其它面形心的变量值
ϕ f 2 = 91.364 , ϕ f 3 = 123.674 , ϕ f 4 = 206.27 , ϕ f 5 = 263.012 , ϕ f 6 = 158.28 \phi_{f_2}=91.364, \quad \phi_{f_3}=123.674, \quad \phi_{f_4}=206.27, \quad \phi_{f_5}=263.012, \quad \phi_{f_6}=158.28 ϕf2=91.364,ϕf3=123.674,ϕf4=206.27,ϕf5=263.012,ϕf6=158.28
计算单元形心C处的梯度值
∇ ϕ C = 1 V C ∑ f = 1 6 ϕ f S ⃗ f = 1 76 { [ 110.442 ( − 6 i + j ) + 91.364 ( 3 i − 4 j ) + 123.674 ( 4 i − 5 j ) + 206.27 ( 5 i − 0.5 j ) + 263.012 ( 3 i + 5.5 j ) + 158.28 ( − 3 i + 3 j ) ] } = 11.889 i + 12.433 j \nabla\phi_C = \frac{1}{V_C}\sum_{f=1}^6\phi_{f} \vec S_f \\ =\frac{1}{76}\left\{ \begin{bmatrix} 110.442(-6\bold i + \bold j)+91.364(3\bold i -4 \bold j)+123.674(4\bold i -5 \bold j) \\ +206.27(5\bold i -0.5 \bold j)+263.012(3\bold i +5.5 \bold j)+158.28(-3\bold i +3 \bold j) \end{bmatrix} \right\} \\ = 11.889 \bold i +12.433 \bold j ∇ϕC=VC1f=1∑6ϕfSf=761{[110.442(−6i+j)+91.364(3i−4j)+123.674(4i−5j)+206.27(5i−0.5j)+263.012(3i+5.5j)+158.28(−3i+3j)]}=11.889i+12.433j
解法b. Green-Gauss方法,含skewness correction, f ′ f' f′选择为线段CF的中点
计算CF的中点 f ′ f' f′处的变量值,使用公式 ϕ f ′ = ( ϕ C + ϕ F ) / 2 \displaystyle \phi_{f'}=(\phi_C+\phi_F)/2 ϕf′=(ϕC+ϕF)/2,得
ϕ f 1 = 111.875 , ϕ f 2 = 101 ϕ f 3 = 123.5 , ϕ f 4 = 209.5 , ϕ f 5 = 261.5 , ϕ f 6 = 159 \phi_{f_1}=111.875, \quad \phi_{f_2}=101 \quad \phi_{f_3}=123.5, \quad \phi_{f_4}=209.5, \quad \phi_{f_5}=261.5, \quad \phi_{f_6}=159 ϕf1=111.875,ϕf2=101ϕf3=123.5,ϕf4=209.5,ϕf5=261.5,ϕf6=159
计算 ∇ ϕ C \nabla\phi_C ∇ϕC使用 ∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f ′ S ⃗ f \displaystyle \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_{f'} \vec S_f ∇ϕC=VC1f−nb(C)∑ϕf′Sf,得
∇ ϕ C = 1 V C ∑ f = 1 6 ϕ f S ⃗ f = 1 76 { [ 111.875 ( − 6 i + j ) + 101 ( 3 i − 4 j ) + 123.5 ( 4 i − 5 j ) + 209.5 ( 5 i − 0.5 j ) + 261.5 ( 3 i + 5.5 j ) + 159 ( − 3 i + 3 j ) ] } = 11.510 i + 11.854 j \nabla\phi_C = \frac{1}{V_C}\sum_{f=1}^6\phi_{f} \vec S_f \\ =\frac{1}{76}\left\{ \begin{bmatrix} 111.875(-6\bold i + \bold j)+101(3\bold i -4 \bold j)+123.5(4\bold i -5 \bold j) \\ +209.5(5\bold i -0.5 \bold j)+261.5(3\bold i +5.5 \bold j)+159(-3\bold i +3 \bold j) \end{bmatrix} \right\} \\ = 11.510 \bold i + 11.854 \bold j ∇ϕC=VC1f=1∑6ϕfSf=761{[111.875(−6i+j)+101(3i−4j)+123.5(4i−5j)+209.5(5i−0.5j)+261.5(3i+5.5j)+159(−3i+3j)]}=11.510i+11.854j
接下来修正梯度值
计算 d ⃗ f = r ⃗ f − r ⃗ C + r ⃗ F 2 \displaystyle \vec d_f = \vec r_f-\frac{\vec r_C+\vec r_F}{2} df=rf−2rC+rF,得
d ⃗ f 1 = − 0.25 i + 0.75 j , d ⃗ f 2 = − 0.5 i − 0.5 j , d ⃗ f 3 = − 0.5 i − 0.25 j , d ⃗ f 4 = − 0.25 i + j , d ⃗ f 5 = − 0.25 i , d ⃗ f 6 = 0.5 i + j \vec d_{f_1}=-0.25\bold i + 0.75\bold j, \quad \vec d_{f_2}=-0.5\bold i -0.5\bold j, \quad \vec d_{f_3}=-0.5\bold i -0.25\bold j, \\ \vec d_{f_4}=-0.25\bold i + \bold j, \quad \vec d_{f_5}=-0.25\bold i, \quad \vec d_{f_6}=0.5\bold i + \bold j df1=−0.25i+0.75j,df2=−0.5i−0.5j,df3=−0.5i−0.25j,df4=−0.25i+j,df5=−0.25i,df6=0.5i+j
更新 ϕ f \phi_{f} ϕf使用 ϕ f = ϕ f ′ + ( ∇ ϕ ) C + ( ∇ ϕ ) F 2 ⋅ ( r ⃗ f − r ⃗ C + r ⃗ F 2 ) \displaystyle \phi_f=\phi_{f'}+\frac{(\nabla\phi)_C+(\nabla\phi)_F}{2}\cdot\left(\vec r_f-\frac{\vec r_C+\vec r_F}{2}\right) ϕf=ϕf′+2(∇ϕ)C+(∇ϕ)F⋅(rf−2rC+rF),得
ϕ f 1 = 115.631 , ϕ f 2 = 91.909 ϕ f 3 = 115.766 , ϕ f 4 = 224.113 ϕ f 5 = 265.564 , ϕ f 6 = 176.554 \phi_{f_1}=115.631, \quad \phi_{f_2}=91.909 \quad \phi_{f_3}=115.766, \quad \phi_{f_4}=224.113 \quad \phi_{f_5}=265.564, \quad \phi_{f_6}=176.554 ϕf1=115.631,ϕf2=91.909ϕf3=115.766,ϕf4=224.113ϕf5=265.564,ϕf6=176.554
计算 ∇ ϕ C \nabla\phi_C ∇ϕC使用 ∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f S ⃗ f \displaystyle \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_{f} \vec S_f ∇ϕC=VC1f−nb(C)∑ϕfSf,得
∇ ϕ C = 11.594 i + 13.781 j \nabla\phi_C = 11.594 \bold i + 13.781 \bold j ∇ϕC=11.594i+13.781j
再迭代一次修正过程,得
∇ ϕ C = 11.652 i + 15.793 j \nabla\phi_C = 11.652 \bold i + 15.793 \bold j ∇ϕC=11.652i+15.793j
如果继续迭代修正,你会发现,这个值压根不会收敛,而且会越来越大直至崩溃,也就是说,修正上一次两次就OK了,既不会浪费时间,也不会让值太离谱了。
方法2:扩展框架
由于面是由角点构成的,所以用角点处的值的平均来算得面形心的值就理所当然了,那么角点处的值要如何获取呢?用围绕该角点的单元形心处的值来加权平均计算即可。比较拗口哈,看下图:

用 F 1 , F 2 , F 3 F_1, F_2, F_3 F1,F2,F3处的值来算得 n 1 n_1 n1处的值,用 F 2 , F 3 , F 4 F_2, F_3, F_4 F2,F3,F4处的值来算得 n 2 n_2 n2处的值,最后再用 n 1 , n 2 n_1,n_2 n1,n2处的值来算得 f f f处的值,即可。
角点处的值由围绕角点的单元形心处的值加权平均算出,加权系数取为距离的倒数(距离越远,影响越小),即
ϕ n = ∑ k = 1 N B ( n ) ϕ F k ∣ ∣ r ⃗ n − r ⃗ F k ∣ ∣ ∑ k = 1 N B ( n ) 1 ∣ ∣ r ⃗ n − r ⃗ F k ∣ ∣ \displaystyle \phi_n=\frac{\displaystyle \sum_{k=1}^{NB(n)}\frac{\phi_{F_k}}{||\vec r_n-\vec r_{F_k}||}}{\displaystyle \sum_{k=1}^{NB(n)} \frac{1}{{||\vec r_n-\vec r_{F_k}||}}} ϕn=k=1∑NB(n)∣∣rn−rFk∣∣1k=1∑NB(n)∣∣rn−rFk∣∣ϕFk
其中 n n n代表角点, F k F_k Fk代表邻近单元, N B ( n ) NB(n) NB(n)为围绕角点 n n n的单元总数, ∣ ∣ r ⃗ n − r ⃗ F k ∣ ∣ ||\vec r_n-\vec r_{F_k}|| ∣∣rn−rFk∣∣为角点到邻近单元形心的距离。
角点值得到后,面形心的值也可得到,以2维问题为例, ϕ f \phi_f ϕf为
ϕ f = ϕ n 1 + ϕ n 2 2 \phi_f=\frac{\phi_{n1}+\phi_{n2}}{2} ϕf=2ϕn1+ϕn2
紧接着,可算得单元形心的梯度 ∇ ϕ C \nabla\phi_C ∇ϕC为
∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f S ⃗ f \displaystyle \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_{f} \vec S_f ∇ϕC=VC1f−nb(C)∑ϕfSf
对于3维情况,面形心的值 ϕ f \phi_f ϕf由角点值的距离加权平均计算,即
ϕ f = ∑ k = 1 n b ( f ) ϕ n k ∣ ∣ r ⃗ f − r ⃗ n k ∣ ∣ ∑ k = 1 n b ( f ) 1 ∣ ∣ r ⃗ f − r ⃗ n k ∣ ∣ \displaystyle \phi_f=\frac{\displaystyle \sum_{k=1}^{nb(f)}\frac{\phi_{n_k}}{||\vec r_f-\vec r_{n_k}||}}{\displaystyle \sum_{k=1}^{nb(f)} \frac{1}{{||\vec r_f-\vec r_{n_k}||}}} ϕf=k=1∑nb(f)∣∣rf−rnk∣∣1k=1∑nb(f)∣∣rf−rnk∣∣ϕnk
而单元形心梯度值的计算方法照旧不变。
例2 与例1数据相同,用方法2:扩展框架计算单元中心梯度值
用方法2:扩展框架计算单元中心梯度值
先计算角点与其周围单元形心的距离值 d n F k = ∣ ∣ r ⃗ n − r ⃗ F k ∣ ∣ d_{nF_k}=||\vec r_n-\vec r_{F_k}|| dnFk=∣∣rn−rFk∣∣,得
d n 1 C = 5 , d n 1 F 6 = 4.472 , d n 1 F 1 = 6.364 d_{n_1C}=5, \quad d_{n_1F_6}=4.472, \quad d_{n_1F_1}=6.364 dn1C=5,dn1F6=4.472,dn1F1=6.364
d n 2 C = 5.831 , d n 2 F 1 = 3.808 , d n 2 F 2 = 5 d_{n_2C}=5.831, \quad d_{n_2F_1}=3.808, \quad d_{n_2F_2}=5 dn2C=5.831,dn2F1=3.808,dn2F2=5
d n 3 C = 6.083 , d n 3 F 2 = 4.472 , d n 3 F 3 = 5.220 d_{n_3C}=6.083, \quad d_{n_3F_2}=4.472, \quad d_{n_3F_3}=5.220 dn3C=6.083,dn3F2=4.472,dn3F3=5.220
d n 4 C = 4.472 , d n 4 F 3 = 5.5 , d n 4 F 4 = 5.099 d_{n_4C}=4.472, \quad d_{n_4F_3}=5.5, \quad d_{n_4F_4}=5.099 dn4C=4.472,dn4F3=5.5,dn4F4=5.099
d n 5 C = 5.408 , d n 5 F 4 = 6.021 , d n 5 F 5 = 6.185 d_{n_5C}=5.408, \quad d_{n_5F_4}=6.021, \quad d_{n_5F_5}=6.185 dn5C=5.408,dn5F4=6.021,dn5F5=6.185
d n 6 C = 6.083 , d n 6 F 5 = 5 , d n 6 F 6 = 5.099 d_{n_6C}=6.083, \quad d_{n_6F_5}=5, \quad d_{n_6F_6}=5.099 dn6C=6.083,dn6F5=5,dn6F6=5.099
用距离倒数作为权系数,由角点周围单元形心值获取角点值,即
ϕ n = ∑ k = 1 N B ( n ) ϕ F k ∣ ∣ r ⃗ n − r ⃗ F k ∣ ∣ ∑ k = 1 N B ( n ) 1 ∣ ∣ r ⃗ n − r ⃗ F k ∣ ∣ \displaystyle \phi_n=\frac{\displaystyle \sum_{k=1}^{NB(n)}\frac{\phi_{F_k}}{||\vec r_n-\vec r_{F_k}||}}{\displaystyle \sum_{k=1}^{NB(n)} \frac{1}{{||\vec r_n-\vec r_{F_k}||}}} ϕn=k=1∑NB(n)∣∣rn−rFk∣∣1k=1∑NB(n)∣∣rn−rFk∣∣ϕFk
得
ϕ n 1 = 131.008 , ϕ n 2 = 79.708 ϕ n 3 = 87.317 , ϕ n 4 = 168.416 ϕ n 5 = 254.144 , ϕ n 6 = 228.840 \phi_{n_1}=131.008, \quad \phi_{n_2}=79.708 \quad \phi_{n_3}=87.317, \quad \phi_{n_4}=168.416 \quad \phi_{n_5}=254.144, \quad \phi_{n_6}=228.840 ϕn1=131.008,ϕn2=79.708ϕn3=87.317,ϕn4=168.416ϕn5=254.144,ϕn6=228.840
计算面形心处的变量值,用面角点值平均来获取,例如 ϕ f 1 = ( ϕ n 1 + ϕ n 2 ) / 2 \phi_{f1}=(\phi_{n1} + \phi_{n2})/2 ϕf1=(ϕn1+ϕn2)/2,得
ϕ f 1 = 105.358 , ϕ f 2 = 83.512 ϕ f 3 = 127.866 , ϕ f 4 = 211.280 ϕ f 5 = 241.492 , ϕ f 6 = 179.924 \phi_{f_1}=105.358, \quad \phi_{f_2}=83.512 \quad \phi_{f_3}=127.866, \quad \phi_{f_4}=211.280 \quad \phi_{f_5}=241.492, \quad \phi_{f_6}=179.924 ϕf1=105.358,ϕf2=83.512ϕf3=127.866,ϕf4=211.280ϕf5=241.492,ϕf6=179.924
计算单元中心梯度值,用 ∇ ϕ C = 1 V C ∑ f − n b ( C ) ϕ f S ⃗ f \displaystyle \nabla\phi_C = \frac{1}{V_C}\sum_{f-nb(C)}\phi_{f} \vec S_f ∇ϕC=VC1f−nb(C)∑ϕfSf,得
∇ ϕ C = 11.446 i + 11.767 j \nabla\phi_C = 11.446 \bold i + 11.767 \bold j ∇ϕC=11.446i+11.767j
3 Least-Square Gradient(最小二乘梯度)
最小二乘法计算梯度,提供了更高的精度,以及更加灵活的选择,用的框架点也更多,然而其需要计算较多的加权系数,当然计算消耗也比较大。
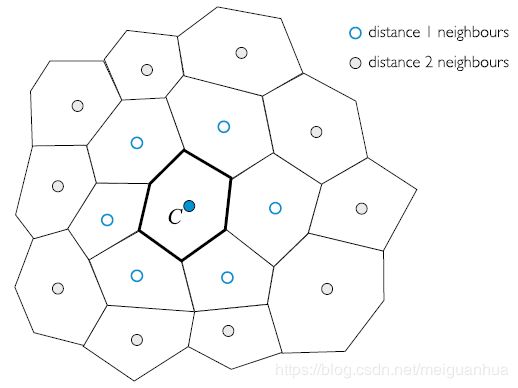
考虑上图,单元 C C C有第1层邻近单元和第2层邻近单元,那么,如果单元形心的梯度 ∇ ϕ C \nabla\phi_C ∇ϕC是精确的话,有
ϕ F = ϕ C + ( ∇ ϕ ) C ⋅ ( r ⃗ F − r ⃗ C ) \phi_F=\phi_C+(\nabla\phi)_C\cdot(\vec r_F - \vec r_C) ϕF=ϕC+(∇ϕ)C⋅(rF−rC)
在最小二乘法中,设法让上式算得的单元邻近单元值的加权加和值最小,即找到如下函数的最小值
G C = ∑ k = 1 N B ( C ) { w k [ ϕ F k − ( ϕ C + ( ∇ ϕ ) C ⋅ r ⃗ C F k ) ] 2 } = ∑ k = 1 N B ( C ) { w k [ Δ ϕ k − ( Δ x k ( ∂ ϕ ∂ x ) C + Δ y k ( ∂ ϕ ∂ y ) C + Δ z k ( ∂ ϕ ∂ z ) C ) ] 2 } G_C=\sum_{k=1}^{NB(C)}\{ w_k[\phi_{F_k}-(\phi_C+(\nabla\phi)_C\cdot\vec r_{CF_k})]^2 \} \\ =\sum_{k=1}^{NB(C)}\left\{ w_k\left[\Delta\phi_k - \left( \Delta x_k\left(\frac{\partial\phi}{\partial x}\right)_C + \Delta y_k\left(\frac{\partial\phi}{\partial y}\right)_C + \Delta z_k\left(\frac{\partial\phi}{\partial z}\right)_C \right) \right]^2 \right\} GC=k=1∑NB(C){wk[ϕFk−(ϕC+(∇ϕ)C⋅rCFk)]2}=k=1∑NB(C){wk[Δϕk−(Δxk(∂x∂ϕ)C+Δyk(∂y∂ϕ)C+Δzk(∂z∂ϕ)C)]2}
其中 w k w_k wk为加权系数
Δ ϕ k = ϕ F k − ϕ C Δ x k = r ⃗ C F k ⋅ i ⃗ Δ y k = r ⃗ C F k ⋅ j ⃗ Δ z k = r ⃗ C F k ⋅ k ⃗ \Delta\phi_k=\phi_{F_k}-\phi_C \\ \quad \\ \Delta x_k=\vec r_{CF_k}\cdot\vec i \\ \quad \\ \Delta y_k=\vec r_{CF_k}\cdot\vec j \\ \quad \\ \Delta z_k=\vec r_{CF_k}\cdot\vec k Δϕk=ϕFk−ϕCΔxk=rCFk⋅iΔyk=rCFk⋅jΔzk=rCFk⋅k
G C G_C GC函数的最小值应满足如下条件
∂ G C ∂ ( ∂ ϕ ∂ x ) = ∂ G C ∂ ( ∂ ϕ ∂ y ) = ∂ G C ∂ ( ∂ ϕ ∂ z ) = 0 \frac{\partial G_C}{\partial \displaystyle \left( \frac{\partial\phi}{\partial x} \right)} = \frac{\partial G_C}{\partial \displaystyle \left( \frac{\partial\phi}{\partial y} \right)} =\frac{\partial G_C}{\partial \displaystyle \left( \frac{\partial\phi}{\partial z} \right)} = 0 ∂(∂x∂ϕ)∂GC=∂(∂y∂ϕ)∂GC