【论文笔记】Graph Transformer Networks
原文摘自我自己的博客Link:http://holdenhu.cn/2020/paper-notegraph-transformer-networks/
题目:《Graph Transformer Network》
作者:Seongjun Yun
来源:NeurIPS2019
源码:Not published yet
笔记:Hu Hengchang
Intro
GTNs(Graph Transformer Networks)的主要功能是在原始图上识别未连接节点之间的有用连接。
Transformer来学习有用的多跳连接,即所谓的元路径。将异质输入图转换为每个任务有用的元路径图,并以端到端方式学习图上的节点表示。
Definition
heterogeneous
异质图:例如,引用网络具有多种类型的节点(例作者、论文、会议)和由它们之间的关系(如作者-论文、论文-会议)定义的边。
homogeneous
同质图,具有一种类型的节点和边的标准图。
Related Work
传统的GNN
是一种两阶段的方法,但每个问题都需要手工构建元路径。这些元路径的选择对下游分析的准确性有很大的影响。
包括spectral和non-spectral两种方法。
-
spectral是基于spectral domain(using Fourier basis)上进行卷积。
-
non-spectral直接在图上沿着edge执行卷积操作。
Contribution
大多数现有的GNNs都被设计为在固定(fix)和同质(homogeneous)的图上学习节点表示。当在不确定的图或由各种类型的节点和边组成的异质(heterogeneous)图上学习表示时,这些限制尤其成问题。一般的GNN手动定义元路径,但GTNs可以学习有效的元路径。
因此GTNs的出现:
-
提出了一种新的图变换网络,识别有用的元路径和多跳连接来学习图上的有效节点表示。
-
图的生成是可解释的,提供有效路径连接的解释。
-
证明了图变换网络学习的节点表示的有效性,从而获得了最佳的性能,而现有的方法在异质图的所有三种基准节点分类中都使用了领域知识。
Implemention
我们的GTNs的目标是生成新的图结构,同时学习到有效的node representation。GTNs使用多个candidate adjacency matrices寻找新的图结构。
preliminaries
-
图表示为 G = ( V , E ) G=(V,E) G=(V,E), V V V is set of nodes, E E E is set of observed edges。
-
T v \mathcal{T}^v Tv和 T e \mathcal{T}^e Te分别表示node的种类,和edge的种类的set。
-
异质图能表示为adjacency matrices的集合 A k k = 1 K {A_k}_{k=1}^K Akk=1K, 其中 K = ∣ T e ∣ K=|\mathcal{T}^e| K=∣Te∣, 它也可以写成Tensor A ∈ R N × N × K \mathbb{A} \in \mathbf{R}^{N \times N \times K} A∈RN×N×K
Meta-path Generation
-
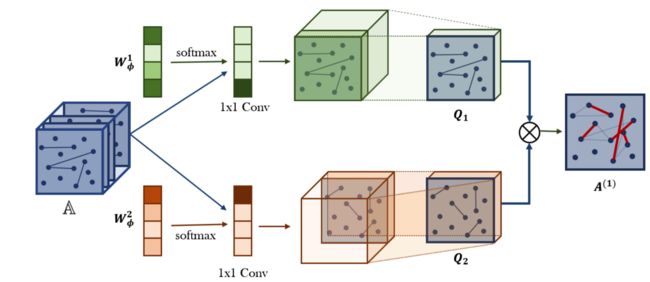
此图即表示GT(Graph Transformer) Layer,它先从tensor A \mathbb{A} A(每一片就是一种edge type)中用权重选择adjacency matrices(即edge type)。权重选择的方式也可以理解成卷积,卷积后的两个matrices分别是两个图解构,表示为 Q 1 Q_1 Q1和 Q 2 Q_2 Q2。
-
选择matrices的两个卷积核是用softmax计算得出的(比如图中例子,一个卷积核说取最前面的matrices,一个卷积核说取最后面那个matrices),但实际上是带有权重分配的。
-
然后再将两个matrices组成新的图结构(即两个邻接矩阵的矩阵乘法, Q 1 Q 2 {Q_1}{Q_2} Q1Q2)。
用数学形式可以表示为:
- 选择的Q可以表示为:
Q = F ( A ; W ϕ ) = ϕ ( A ; softmax ( W ϕ ) ) Q=F\left(\mathbb{A} ; W_{\phi}\right)=\phi\left(\mathbb{A} ; \operatorname{softmax}\left(W_{\phi}\right)\right) Q=F(A;Wϕ)=ϕ(A;softmax(Wϕ))
即得出的 Q Q Q是将 A \mathbb{A} A和权重参数 W ϕ W_{\phi} Wϕ送去convolution layer卷积得到的
- 每一个 Q i Q_i Qi可以表示成:
∑ t l ∈ T e α t l ( l ) A t l \sum_{t_{l} \in \mathcal{T}^{e}} \alpha_{t_{l}}^{(l)} A_{t_{l}} tl∈Te∑αtl(l)Atl
其中 T e \mathcal{T}^e Te是edge的类型集合, α t l ( l ) \alpha_{t_{l}}^{(l)} αtl(l)是edge第 l l l种类型 t l t_l tl在第 l l l层的权重。
以图中为例: T e \mathcal{T}^e Te有4个{ t 1 , t 2 , t 3 , t 4 t_1,t_2,t_3,t_4 t1,t2,t3,t4}, 即对应4层matrices: { A 1 , A 2 , A 3 , A 4 A_1,A_2,A_3,A_4 A1,A2,A3,A4}, W ϕ W_{\phi} Wϕ={ α 1 , α 2 , α 3 , α 4 α_1,α_2,α_3,α_4 α1,α2,α3,α4}
- 如果不是分两个Q,而是多个,则最后得到的结果新A可表示为:
A P = ( ∑ t 1 ∈ T e α t 1 ( 1 ) A t 1 ) ( ∑ t 2 ∈ T e α t 2 ( 2 ) A t 2 ) . . . ( ∑ t l ∈ T e α t l ( l ) A t l ) A_P = \left(\sum_{t_{1} \in \mathcal{T}^{e}} \alpha_{t_{1}}^{(1)} A_{t_{1}}\right)\left(\sum_{t_{2} \in \mathcal{T}^{e}} \alpha_{t_{2}}^{(2)} A_{t_{2}}\right)...\left(\sum_{t_{l} \in \mathcal{T}^{e}} \alpha_{t_{l}}^{(l)} A_{t_{l}}\right) AP=(t1∈Te∑αt1(1)At1)(t2∈Te∑αt2(2)At2)...(tl∈Te∑αtl(l)Atl)
Multi-channel
为了同时生成多种类型的元路径,图1中1×1卷积的输出通道设置为C。
然后,GT层产生一组meta-path,中间邻接矩阵Q1和Q2成为邻接张量 Q 1 \mathbb{Q}_1 Q1和 Q 2 ∈ R N × N × C \mathbb{Q}_2 \in \mathbf{R}^{N \times N \times C} Q2∈RN×N×C,如图2所示。通过多个不同的图结构学习不同的节点表示是有益的。在 l l l个GT层堆栈之后,将GCN应用于元路径张量 A l ∈ R N × N × C \mathbb{A}^{l} \in \mathbf{R}^{N \times N \times C} Al∈RN×N×C的每个通道,并将多个节点的representation拼接起来。
结果 Z Z Z的生成可表示为:
Z = ∥ ∥ i = 1 C σ ( D ~ i − 1 A ~ i ( l ) X W ) Z=\|\|_{i=1}^{C} \sigma\left(\tilde{D}_{i}^{-1} \tilde{A}_{i}^{(l)} X W\right) Z=∥∥i=1Cσ(D~i−1A~i(l)XW)
其中 ∣ ∣ || ∣∣是concatenation操作。 C C C表示channel数量。 A i l ~ = A i l + I \tilde{A_{i}^{l}}=A_{i}^{l}+I Ail~=Ail+I, 表示张量 A ( l ) \mathbb{A}^{(l)} A(l)的第 l l l个通道。 D i ~ \tilde{D_i} Di~是 A i ~ \tilde{\mathbb{A}_i} Ai~的degree matrix, W ∈ R d × d W \in \mathbf{R}^{d \times d} W∈Rd×d 是训练权重矩阵, X ∈ R N × d X \in \mathbf{R}^{N \times d} X∈RN×d表示特征矩阵。
Evaluation
研究问题:
-
Q1:GTN生成的新图结构对学习node representation是否有效?
-
Q2:GTN能否根据数据集自适应地产生可变长度的元路径?
-
Q3:如何从GTNs生成的邻接矩阵来解释每个元路径的重要性?
Dataset
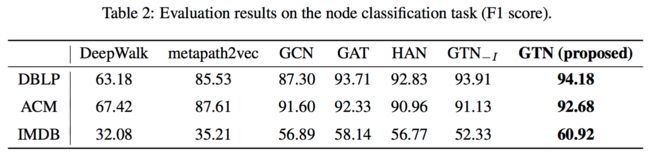
GTN和其他节点分类基线的性能
可以看到GTNs获得最高性能。
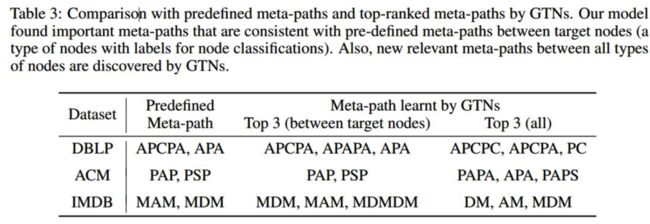
可解释元路径
Note: 这里的不同字母表示不同种类的node.