【机器学习系列1】线性回归LinearRegression——数学推导和纯Numpy实现

这一系列是学习公众号“机器学习实验室”的笔记，跟着大佬的脚步一个个实现。

数学推导

notations

$X=\{x_i,i=1,2,...,m\}X\subseteq {\mathbb{R}}^{m\times d}$
$x_i=(x_{i1},x_{i2},...,x_{id})x_i\subseteq {\mathbb{R}}^{1\times d}$
$Y=\{y_i,i=1,2,...,m\}Y\subseteq {\mathbb{R}}^{m\times 1}$
$y_i\subseteq \mathbb{R}$

objective function

$(W^{\star },b^{\star })=\underset{(w,b)}{\mathrm{argmin}}{\sum }_{i=1}^m(F(x_i)-y_i{)}^2$

partial derivative

$\frac{\partial E(w,b)}{\partial w}=2({\sum }_{i=1}^m{x}_{i}w-{\sum }_{i=1}^m{x}_i(y_i-b))$

$\frac{\partial E(w,b)}{\partial b}=2({\sum }_{i=1}^m(w{x}_i-y_i)-mb)$

$dw=\frac{{\sum }_{i=1}^m(y_i-b)x_i}{{\sum }_{i=1}^m{x}_i}$

$db=\frac{{\sum }_{i=1}^m(w{x}_i-y_i)}{m}$

matrix version

我们利用Numpy实现，数据存放为二维数组，在代码实现的时候需要看一下矩阵相乘合不合法。

手动实现线性回归

首先分析有几个部分：LinearRegression作为一个类，应该满足喂入训练数据x和y，然后拟合好一个线性函数F，参数为W和b；此外根据这个线性函数可以预测我们的测试数据。
由此我们可以很快想到造一个训练器train、一个预测器predict和一个评价器evaluation。
下面我们按着思路设计。

训练器 train

思路

1. 训练器的input是x_train和y_train，output是weight和bias。
2. 优化思想是最小二乘，出发点是最小均方差，这样loss就可以确定为$\frac{1}{m}{\sum }_{i=1}^m(\widehat{y_i}-y_i{)}^2$，其中的$\frac{1}{m}$作为常数可以省略。
3. 考虑到特征维数较高，就不用正规方程解法，直接用数值优化方法——梯度下降，对loss函数求导见上。
   因此我们可以写出伪代码：

initialize parameters w, b
for epoch in epochs:
	caculate loss, dw, db
	update w with dw
	update b with db
	return w, b

第一步是初始化参数，权重与特征维数一致，偏差是个常数。
第二步是求loss和偏导，我们可以通过一个函数完成。这个函数要求输入x_train，y_train和参数，返回loss，dw，db。
第三步就是利用返回的偏导更新参数，在这里可以加入早停，因为目标函数是个凸函数，只要发现loss变大就暂停。

代码实现

接下来我们来实现训练器，我在训练后调整训练率、偏差初始值调整模型。

# 初始化
def initialize_params(self, dims):
    W = np.zeros((dims,1))
    b = 150
    return W, b

# 求loss,dw,db
def loss(self, X, y, W, b):
	# 对Numpy不太熟悉，点除直接写成一个函数
    def dot_division(dW, dsum):
        for i in range(len(dW)):
            dW[i] /= dsum[i]
        return dW
    
    num_train = X.shape[0]
    num_feature = X.shape[1]
	
	# 求y_hat,loss,dw,db
    y_hat = np.dot(X, W) + b
    loss = np.sum((y - y_hat)**2) / num_train

    db = np.sum(y - y_hat) / num_train
    dsum = np.sum(X.T, axis=1)
    dW = np.dot(X.T,(y - db))
    dW = dot_division(dW, dsum)
    return y_hat, loss, dW, db

def train(self, X, y, learning_rate, epochs):
    # 初始化参数
    dims = X.shape[1]
    W, b = self.initialize_params(dims)
	
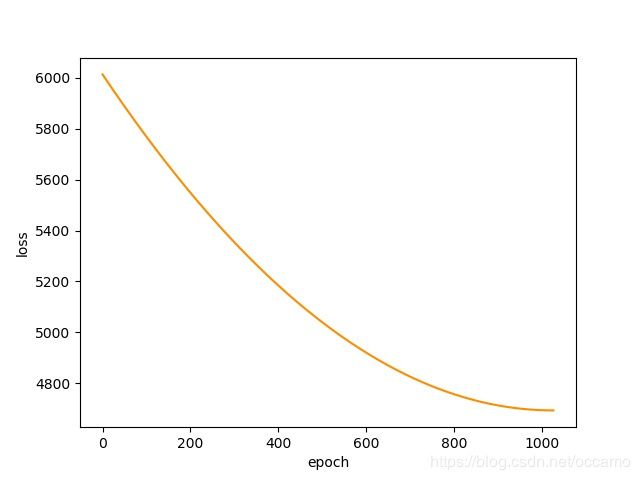
	# 存放loss值，方便查看loss变化，并设定loss最小值，如果变大就停止
    loss_list = []
    loss_min = np.inf
    
    for epoch in range(epochs):
        y_hat, loss, dW, db = self.loss(X, y, W, b)

        loss_list.append(loss)
        if loss < loss_min:
            loss_min = loss
        else:
            print("EarlyStop.")
            break

        if epoch % 10000 == 0:
            print("epoch %d loss %f" %(epoch, loss))

        W += learning_rate * dW
        b += learning_rate * db
         
        params = {
            'W':W,
            'b':b
        }

        grads = {
            'dW':dW,
            'db':db
        }

    return loss_list, loss, params, grads

预测器 predict

思路

input是存放的使loss最小的parameters和x_test，output是计算得到的y_predict。
这个比较简单，直接上代码。

代码

def predict(self, X, params):
    W = params['W']
    b = params['b']
    y_predict = np.dot(X, W) + b
    return y_predict

评价器 evaluation

思路

input是预测得到的值y_predict和原值y_test，output是我们定义的均方误差，均方根误差，平均绝对误差，R平方值。

代码

def evalution(self, y_predict, y):
    m = y.shape[0]
    mse = np.sum((y_predict - y)**2) / m
    rmse = mse**0.5
    mae = np.sum(np.absolute(y_predict - y)) / m
    r2 = 1 - (mse / np.var(y))
    return mse, rmse, mae, r2

到此我们的模块分析就完成了，接下来完整数据处理代码和其他代码。

数据处理

我参照了公众号的代码，利用shuffle打乱数据，然后取10%的测试集，剩下的用来训练。

代码

def pre_data_init(self):
        data = load_diabetes().data
        target = load_diabetes().target
        X, y = shuffle(data, target, random_state=42)
        X = X.astype(np.float32)
        y = y.reshape((-1,1))
        
        offset = int(X.shape[0] * 0.9)
        x_train, y_train = X[:offset], y[:offset]
        x_test, y_test = X[offset:], y[offset:]

        y_train = y_train.reshape((-1,1))
        y_test = y_test.reshape((-1,1))
        
        return x_train, x_test, y_train, y_test

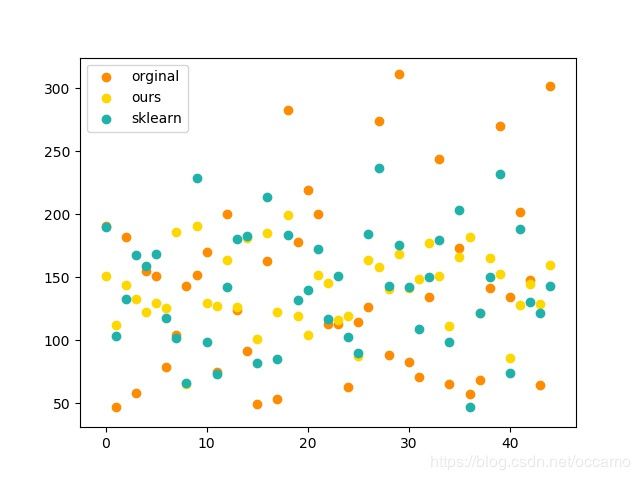
与sklearn比较

我加入sklearn的包来比较模型的效果，虽然效果不够好，但是已经具备初始形状了。

sklearn: mse: 3409.542078, rmse: 58.391284, mae: 47.374929, r2: 0.341719
ours: mse: 4637.266031, rmse: 68.097474, mae: 58.506708, r2: 0.104682

完整代码

https://github.com/oneoyz/ml_algorithms/tree/master/linear_regression