【机器学习系列3】K近邻算法KNearestNeignbors——思路推导和纯Numpy实现

这一系列是学习公众号“机器学习实验室”的笔记，跟着大佬的脚步一个个实现，今天实现的是kNN，kNN是一个思想比较简单的监督算法，没有数学推导，计算的东西比较多，因此我将数学推导换成思路推导来考虑怎么写代码。

思路推导

kNN的思想

没有预训练这些过程，kNN单纯是暴力求距离，然后统计k个距离近的样本的标签，谁多听谁的，显而易见这是个近邻匹配的思想。我之前总结过优化思想和出发点：

优化思想	出发点
最小二乘法	最小均方差
最大似然法	最大似然概率

近邻匹配的出发点就是用相似的个体进行投票，我们把重点放在代码上。

手动实现kNN

首先分析有几个部分：KNearestNeignbors作为一个类，应该满足喂入训练数据x和y，然后放入要预测的测试样本，并不经过训练，直接计算这个样本和所有训练样本的距离，统计k个距离最近的样本的标签，最多的标签设为该样本的标签。值得注意的是，我们在计算距离的时候是放入整个矩阵的，因此这个地方需要设计计算的代码。
由此我们可以很快想到造一个计算距离distant、一个预测器predict和一个评价器evaluation，在这里我还加入了一个交叉验证validation
代码如果有不对的还请指正。

计算距离 distant

思路

1. 在这里我设计了两个距离，一个是向量2-范数，一个是余弦相似度cosine。
2. 这两个公式都比较熟悉，$l_2=\sqrt{(x-y{)}^2}$，在矩阵中则需要一些技巧。首先先考虑两个矩阵计算，最后我们想要得到的是$n_1\times n_2$大小的矩阵，分别为测试集和训练集的大小，因为从测试集$n_1$出发要知道和每一个训练集样本的距离。

   • 分解后先是求$x-y$，因为一共需要求$n_1\times n_2$个距离，我分别把两个矩阵扩展到这个大小，直接减后再reshape。以测试集为例，大小为$n_1\times d$，先是reshape为$(n_1,1,d)$的张量，这样用tile扩展的时候就可以形成连续相同样本。
     例：

     $a=array([1,2,3],[4,5,6])(2\times 3)$
     $b=array([1,2,1],[6,7,9],[8,2,0],[7,1,4],[9,3,1])(5\times 3)$
     $tile(a,(5,1))=array([1,2,3],[4,5,6],[1,2,3],[4,5,6],[1,2,3],[4,5,6],[1,2,3],[4,5,6],[1,2,3],[4,5,6])(10\times 3)$
     转换为$array([[[1,2,3]],[[4,5,6]]])$后
     $tile(a,(1,5,1))=array([[1,2,3],[1,2,3],[1,2,3],[1,2,3],[1,2,3]],[[4,5,6],[4,5,6],[4,5,6],[4,5,6],[4,5,6]])(2\times 5\times 3)$

   • 这样直接扩展训练集为$(n_1\ast n_2)\times d$，相减在reshape就可以得到$n_1\times n_2$的矩阵，每一行是一个测试样本与所有训练样本的距离。

3. 再看余弦相似性$\frac{x\cdot y}{\Vert x\Vert \Vert y\Vert }$，上面的部分是一个向量点积，用dot可以实现，下面是一个常数。我们看$\Vert x\Vert$可以写成这个向量每个值先平方，然后按行方向求和，同理求得$\Vert y\Vert$，分别按行和按列扩展至大小一致，相减完事了！
   

代码实现

def distant(self, x_tr, x_test, dis_type):
	if dis_type == 'l2':
        dim_tr = x_tr.shape[0]
        dim_te = x_test.shape[0]
        dim_feature = x_tr.shape[1]

        # l2 = ((x - y)**2)**0.5
        # expand_tr = x_tr.reshape((-1, dim_te))
        ## calculate x - y through tile(), and the square root of sum
        expand_te = np.tile(x_test.reshape((dim_te,1,-1)), (1 ,dim_tr,1))
        expand_te = expand_te.reshape((-1, dim_feature))
        expand_tr = np.tile(x_tr,(dim_te,1))
        dist_xy = np.sum((expand_te - expand_tr)**2, axis=1)
        dist_mat = (dist_xy**0.5).reshape((dim_te,-1))
        return dist_mat

    if dis_type == 'cosine':
        # dimension of sets
        dim_tr = x_tr.shape[0]
        dim_te = x_test.shape[0]

        # cos = A.T.dot(B) / ((A**2)**0.5 + (B**2)**0.5)
        ## calculate the dot product, and the sqaure root of x and y
        frac_u = np.dot(x_test, x_tr.T)
        sub_tr = (x_tr**2).sum(axis=1).reshape((-1,1))
        sub_tr = np.tile(sub_tr.T**0.5,(dim_te, 1))
        sub_te = (x_test**2).sum(axis=1).reshape((-1,1))
        sub_te = np.tile(sub_te**0.5,(dim_tr))
        frac_d = sub_tr * sub_te
        return frac_u / frac_d

预测器 predict

思路

在这里调用distant计算距离，然后对每一行利用argsort排序，函数将排名和索引联系起来了。对每一个测试样本，取前k个的索引，查看其标签，将标签放入字典中。对着k个统计完后，计算字典里的最多投票。这个结构要清晰：

initialize prediction list
for sample in shape[0]:
	initialize dictionary
	for i in range(k):
		look up labels
		put into dictionary
	sort dictionary
	append the label into the prediction list
return prediction list

代码

def predict(self, x_tr, y_tr, x_test, y_test, k):
    dist_mat = self.distant(x_tr, x_test, 'cosine')
    dist_k = dist_mat.argsort(axis=1)
    y_predict = np.array([])
    
    for sample in range(dist_k.shape[0]):
        class_count = {}
        for i in range(k):
            vote_label = int(y_tr[dist_k[sample][i]])
            class_count[vote_label] = class_count.get(vote_label, 0) + 1

        final_vote = sorted(class_count.items(), 
            key=operator.itemgetter(1), reverse=True)
        y_predict = np.append(y_predict, final_vote[0][0])

    y_predict = y_predict.reshape((-1,1))
    return y_predict

评价器 evaluation

思路

和逻辑回归的一样，都是分类的评价标准：准确率，精确率，召回率。

代码

def evalution(self, y_predict, y):
	y_test = y_test.ravel()
	y_predict = y_predict.ravel()
	
	num_test = y_test.shape[0]
	# succeed: 0  fail: 1,-1
	outcome = y_predict - y_test
	# succeed: 0  fail: 1
	outcome[outcome == -1] = 1
	
	Counter(outcome)
	Counter(y_predict)
	num_tp_tn = sum(outcome==0)
	num_fp = np.dot(y_predict.T, outcome)
	num_tp = sum(y_predict==1) - num_fp
	num_tn = num_tp_tn - num_tp
	num_fn = sum(y_predict==0) - num_tn
	
	accuracy =  num_tp_tn / num_test
	precision = num_tp / (num_tp + num_fp)
	recall = num_tp / (num_tp + num_fn)
	
	return accuracy, precision, recall

交叉验证 validation

思路

这里我加了一个交叉验证，将训练集又分为训练集和验证集。主要加深了我对numpy的array结构和迭代器yield的理解，可以将这个数组分为几组（整除情况下），取其中的一个组，将剩下的concatnate起来，然后用yield返回一个迭代器，共fold个迭代器（n fold）。每个迭代器里面分别是训练集数据、标签和验证机数据、标签。

代码

def validation(self, x_train, y_train, fold):
     dims = x_train.shape[1]
     if x_train.shape[0] % fold == 0:
         x_fold = []
         y_fold = []
         x_fold = np.split(x_train, fold)
         y_fold = np.split(y_train, fold)
         for i in range(fold):
             x_tr = np.concatenate(
                 (np.array(x_fold)[:i], np.array(x_fold)[i+1:]),axis=0)
             y_tr = np.concatenate(
                 (np.array(y_fold)[:i], np.array(y_fold)[i+1:]), axis=0)
             x_val = np.array(x_fold)[i]
             y_val = np.array(y_fold)[i]
             x_tr = x_tr.reshape((-1,dims))
             y_tr = y_tr.reshape((-1,1))
             yield (x_tr, y_tr, x_val, y_val)
     else:
         print("Attention: vary size.")

在主代码里直接迭代使用

for i, (x_tr, y_tr, x_val, y_val) in enumerate(model.validation(x_train, y_train, 4)):
        print(i)
        y_predict = model.predict(x_tr, y_tr, x_val, y_val, k)

与sklearn比较

我加入sklearn的包来比较模型的效果，在k为10，使用l2距离和包效果一样，但是cosine距离就差很多。
l2在验证集

0
our: 0.96875 0.9634146341463414 0.9875
sklearn: 0.96875 0.9634146341463414 0.9875
1
our: 0.96875 0.9767441860465116 0.9767441860465116
sklearn: 0.96875 0.9767441860465116 0.9767441860465116
2
our: 0.90625 0.9166666666666666 0.9390243902439024
sklearn: 0.90625 0.9166666666666666 0.9390243902439024
3
our: 0.8984375 0.8831168831168831 0.9444444444444444
sklearn: 0.8984375 0.8831168831168831 0.9444444444444444

cosine在验证集

0
our: 0.125 0.0 0.0
sklearn: 0.96875 0.9634146341463414 0.9875
1
our: 0.1171875 0.034482758620689655 0.011627906976744186
sklearn: 0.96875 0.9767441860465116 0.9767441860465116
2
our: 0.203125 0.0 0.0
sklearn: 0.90625 0.9166666666666666 0.9390243902439024
3
our: 0.25 0.038461538461538464 0.013888888888888888
sklearn: 0.8984375 0.8831168831168831 0.9444444444444444

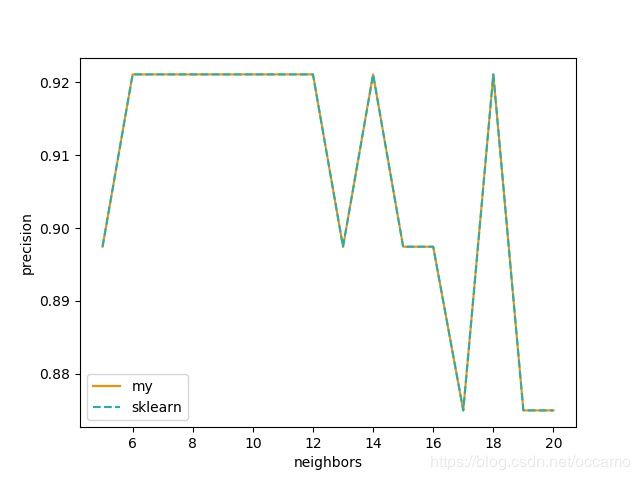
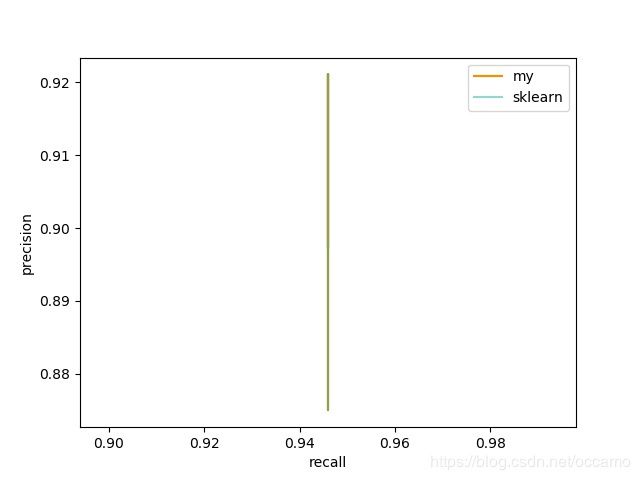
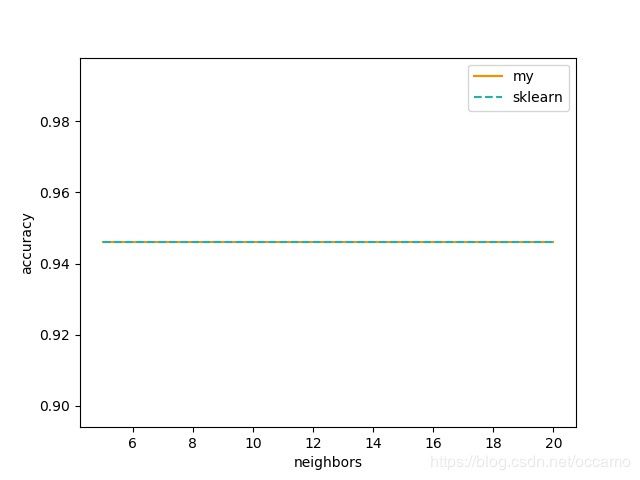
k的影响

k从5到20，准确率、召回率没有变，精确率会震荡。

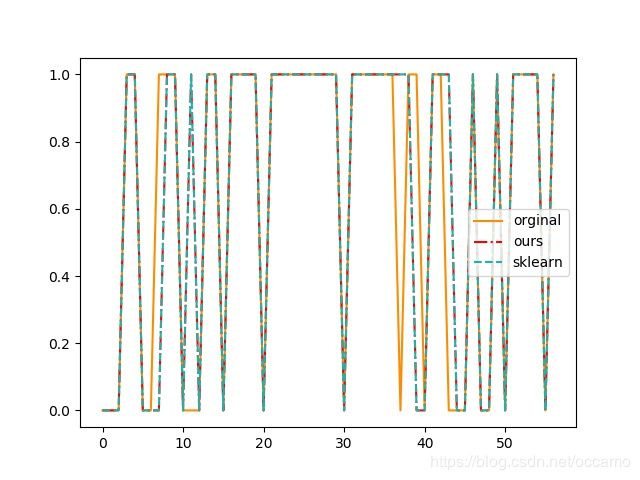
预测效果

完整代码

https://github.com/oneoyz/ml_algorithms/tree/master/k_neighbors