可视化图解Python科学计算包NumPy
点击上方“Python爬虫与数据挖掘”,进行关注
回复“书籍”即可获赠Python从入门到进阶共10本电子书
今
日
鸡
汤
落地为兄弟,何必骨肉亲!
得欢当作乐,斗酒聚比邻。
NumPy包是python生态系统中数据分析、机器学习和科学计算的主力。它极大地简化了向量和矩阵的操作。Python的一些主要软件包依赖于NumPy作为其基础架构的基础部分(例如scikit-learn、SciPy、pandas和tensorflow)。我们将介绍一些使用NumPy的主要方法,以及在我们为机器学习模型提供服务之前它如何表示不同类型的数据(表格、声音和图像)。
import numpy as np一、数组操作
1.1创建数组
通过将python列表传递给NumPy对象,使用np.array()创建一个NumPy数组(即ndarray)。Python创建了我们在右边可以看到的数组:
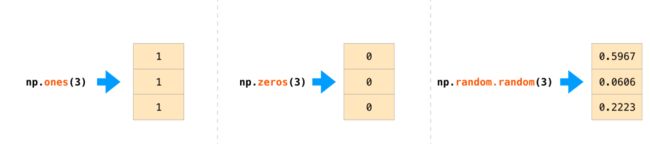
一般情况,我们希望直接使用NumPy作为初始化的数组数据。NumPy为这些情况提供了诸如ones(),zeros()和random.random()类等方法。我们只需要向这些方法传递要生成的元素数量的参数:
一旦我们创建了数组,我们就可以开始以有趣的方式操作它们。
1.2 数组算术
先来创建两个NumPy数组来展示它们的用处。我们称之为data和ones:
这两个数组的加法就像我们+1那么简单(每一行相加)。
可以发现这样的计算不必在循环中实现。这是非常好的抽象处理,可以让你在更高层次上思考问题,而不是陷入如何实现计算的算法里面。
我们还可以像下面一样进行其他运算:
通常情况下,我们希望在数组和单个数字之间执行操作(我们也可以将其称为向量和标量之间的操作)。比如说,我们的数组表示以英里为单位的距离,我们希望将其转换为公里数。我们只需要让数据* 1.6就可以了。
NumPy让每个单元格都会发生相乘叫做广播。
1.3索引数组
我们可以索引、切片NumPy数组。
1.4 数组聚合
NumPy为我们提供非常好用的聚合功能:
除了最小值、最大值和总和之外,还得到非常棒的东西,比如平均值、所有元素相乘的结果、标准差,以及其他很多。
二、多维处理
2.1 创建矩阵
所有的例子都在一个维度上处理向量。NumPy的厉害之处是能够将我们目前所看到的所有内容应用到任意维度上。我们可以传递一个Python列表,让NumPy创建一个矩阵来表示它们:
np.array([[1,2],[3,4]])我们也可以使用上面提到的相同方法(ones(),zeros()和random.random()),只要我们给它们一个元组来描述我们正在创建的矩阵的维度:
2.2 矩阵算术
如果两个矩阵的大小相同,我们可以使用算术运算符(+ - * /)来进行矩阵计算。NumPy将这些作为位置操作处理:
只有当不同维度为1时(例如矩阵只有一列或一行),我们才能在不同大小的矩阵上进行这些算术运算,在这种情况下,NumPy将其广播规则用于该操作:
2.3 点积
NumPy为每个矩阵提供了一个dot()方法,我们可以用它来执行与其他矩阵的点积运算:
两个矩阵在它们彼此面对的一侧必须具有相同的尺寸(上图底部红色的数字)。
2.4 矩阵索引
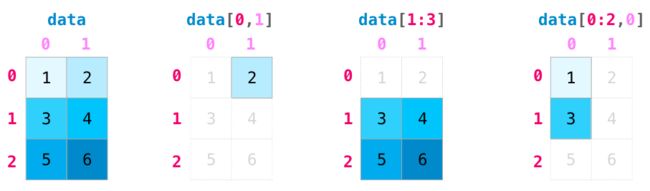
当我们操作矩阵时,索引和切片操作变得更加有用:
冒号表示从哪个位置到哪个位置,留空表示开头或者结尾;逗号表示行和列。NumPy的索引是从0开始的,并且后面的方括号是不包含后面的值(即小于后面的值)。
2.5 矩阵聚合
我们可以像聚合向量一样聚合矩阵:
我们不仅可以聚合矩阵中的所有值,还可以使用axis参数在行或列之间进行聚合:
2.6 转置和重塑
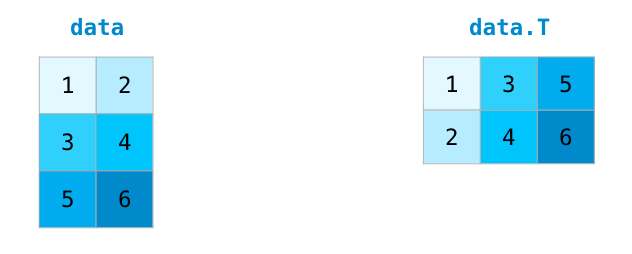
处理矩阵时的一个共同需求是需要旋转矩阵。当我们需要采用两个矩阵的点积并需要对齐它们共享的维度时,通常就是这种情况。NumPy数组有一个方便的属性叫做T来获得矩阵的转置:
在更高级的应用中,您可能会发现自己需要切换某个矩阵的维度。在机器学习应用程序中通常就是这种情况,其中某个模型期望输入的某个形状与您的数据集不同。在这些情况下,NumPy的reshape()法很有用。您只需将矩阵所需的新尺寸传递给它即可。
2.7 更多维度
NumPy可以完成我们在任何维度定义数据。其中心数据结构称为ndarray(N维数组)。
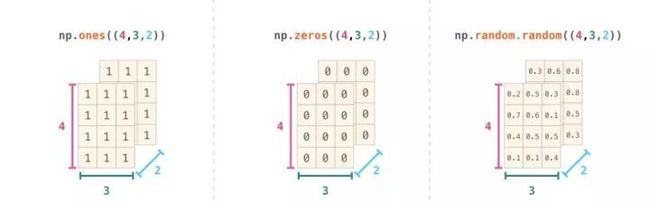
在很多方面,处理新维度只需在NumPy函数的参数中添加逗号:
三、公式计算
我们举一个计算均方误差的例子。实现适用于矩阵和向量的数学公式是考虑NumPy的关键用例。例如均方误差MSE公式,它是监督机器学习、模型处理、回归问题的核心公式:
在NumPy中实现这一点是轻而易举的:
这样做的好处是我们不需要关心predictions和labels是否包含一个或一百个值(只要它们的大小相同)。我们可以通过一个示例逐步执行该代码行中的四个操作:
predictions和labels向量都包含三个值。这意味着n的值为3。在我们执行减法后,我们最终得到如下值:
然后我们可以对矢量中的值进行平方:
然后求和:
结果就是均方误差。
四、数据表示
4.1 表格和电子表格
构建模型所需的所有数据类型(电子表格、图像和音频等),很多都非常适合在n维数组中表示。
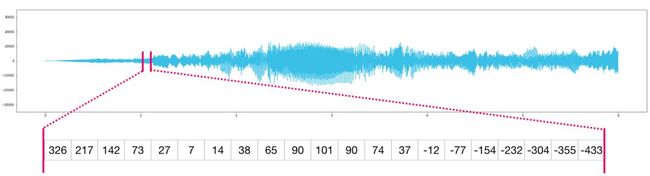
4.2 音频
音频文件是一维样本数组。每个样本都是一个代表音频信号的一小部分的数字。CD质量的音频每秒可能有44,100个样本,每个样本是-65535到65536之间的整数。这意味着如果你有一个10秒的CD质量的WAVE文件,你可以将它加载到长度为10 * 44,100的NumPy数组中 = 441,000个样本。想要提取音频的第一秒?只需将文件加载到我们称之为audio的NumPy数组中,然后获取audio[:44100]。
4.3 图像
图像是高度×宽度的像素矩阵。
如果图像是黑白的(即灰度),则每个像素可以由单个数字表示(通常在0(黑色)和255(白色)之间)。想要裁剪图像的左上角10 x 10像素部分?告诉NumPy让你image[:10,:10]。
如果图像是彩色的,则每个像素由三个数字表示(RGB)。在这种情况下,我们需要第三维(因为每个单元格只能包含一个数字)。因此彩色图像由尺寸的ndarray表示:(高x宽x 3)。
------------------ End -------------------
![]()
想加入Python学习群请在后台回复【入群】
万水千山总是情,点个【在看】行不行