第k个排列(C++)

给出集合 [1,2,3,…,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

1. "123"
2. "132"
3. "213"
4. "231"
5. "312"
6. "321"

给定 n 和 k，返回第 k 个排列。

说明：

• 给定 n 的范围是 [1, 9]。
• 给定 k 的范围是[1,  n!]。

示例 1:

输入: n = 3, k = 3
输出: "213"

示例 2:

输入: n = 4, k = 9
输出: "2314"

【解题思路】

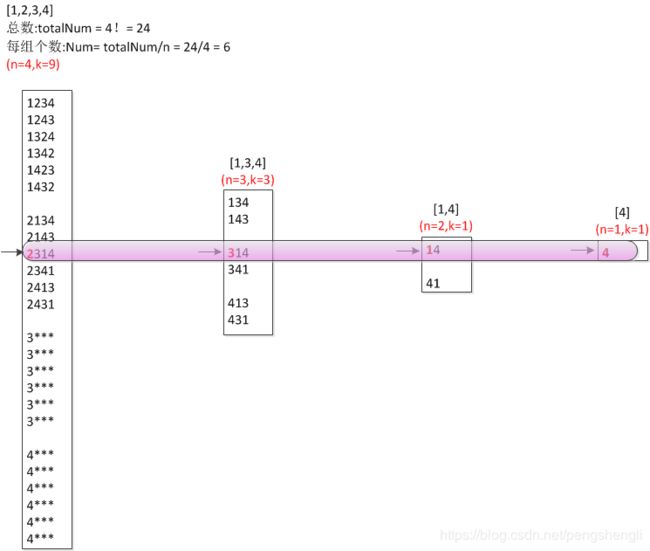
先以n=4,k=9为例，看下图：

有没有发现什么规律？

1.n!种排列中的顺序可以分为（n!/n）组，其中每组的第一个数字都一样；

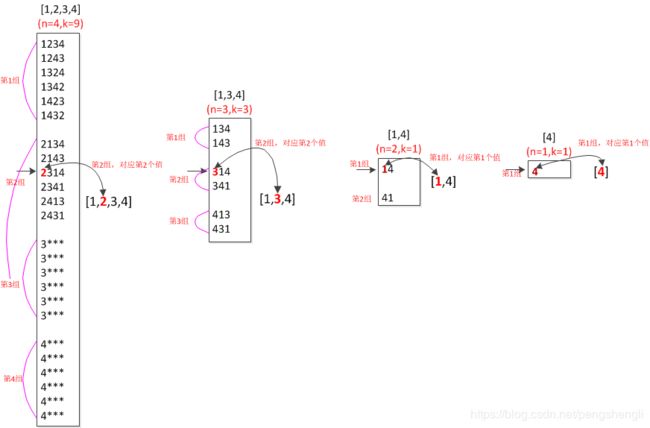
2.通过k求出该序列落在第几组，比如，上图n=4,k=9,就落在第二组，那该序列的第一个元素就是数组的第二个元素--2；

3.第一个元素确定后，把数组的这个数抠掉，比如，上面2已经确定了，就把2扣掉，数组就剩3个元素了---[1,3,4]。注意：抠掉后，数组仍然要保持有序。

4.当第一个元素确定后，数组就变成3个元素，k变成了3，即n=3,k=3。数组为[1,3,4]，再重复上面的步骤，就可求出第二个元素是3，在抠掉3。

问题关键在于怎么计算下一次的落在第几组和k。

#include"stdafx.h"
#include
#include
#include
using namespace std;
int getgroup(int num, int k)//num为每个组元素个数；
{
	if (k % num == 0) return k / num;
	else
		return k / num + 1;
}
int getk(int num, int k)
{
	if (k < num) return k;
	else
	{
		if (k % num == 0)
			return num;
		else
			return k % num;
	}		
}
string getPermutation(int n, int k) {
	if (n < 1) return "";
	int count = 1;//n!总共排列数量
	vector vct;
	string res("");
	for (int i = 1; i <= n; i++)
	{
		vct.push_back(i);
	}
	for (int i = 1; i <= n; i++)
	{
		count *= i;
	}
	while (n > 0)
	{
		//每组的个数
		int num = count / n;
		//落在哪一组
		int group = getgroup(num, k);
		//计算下一次的k值
		k = getk(num, k);
		//结果追加到字符串
		res += vct[group - 1] + '0';
		//下一次的序列总数
		count /= n;
		//删除元素
		vct.erase(vct.begin() + group - 1);
		n--;
	}
	return res;
}
int main()
{
	getPermutation(4, 9);
	getPermutation(3, 6);
	getPermutation(3, 1);
	getPermutation(3, 2);
	return 0;
}

解释一下：

1.n有序数放在vector,主要是删除指定位置的元素好操作；

2.最核心的是求出group，因为知道group就知道给字符串追加哪个数字了，

int getgroup(int num, int k)//num为每个组元素个数；
{
	if (k % num == 0) return k / num;
	else
		return k / num + 1;
}

举例：n=4,k=9

count = 24，共n=4组，每组num=6个序列，第9个应该落在 第（9 / 6+1）=2组上，所以就把当前数组[1,2,3,4]的第二个（2）数追加到字符串上，然后把 "2"从数组中去掉，数组变为[1,3,4].

需要注意的是：k能被num整除时是特殊处理，比如上面的例子（n=4,k=12）那么group=12/2=2,就是在第二组，不需要加1了。

还有这里k不会等于0,所以不用考虑k=0的情况。

3.本次的值追加到字符串后，就需要计算下一次k的值

int getk(int num, int k)
{
	if (k < num) return k;
	else
	{
		if (k % num == 0)
			return num;
		else
			return k % num;
	}		
}

如上图，从n=4,k=9 变为 n=3,k=3;这是怎样一个过程？