TRAINING AND INFERENCE WITH INTEGERS IN DEEP NEURAL NETWORKS
本篇文章主要创新点在于不仅仅提供了对activation 和weights的量化,还通过同样的方式,对gradient和error进行了量化。将模型的量化做的更加深入。
这篇文章主要分为两块,第一块是知识铺垫,第二块是四个量化
知识铺垫
MACs(矩阵乘法)会导致量化bit增加

K指量化的bit数。这个图比较难理解的地方在于右边。 [ k E + k A − 1 ] [k_{E}+k_{A}-1] [kE+kA−1] 和 [ k E + k w − 1 ] [k_{E}+k_{w}-1] [kE+kw−1]是怎么得到的。
其实就是根据bp 过程分析出来的。以第一个为例,

根据这个公式,其中 a k l − 1 a_{k}^{l-1} akl−1的精度是 k A k_{A} kA, δ j l \delta_{j}^{l} δjl的精度是 k E k_{E} kE由此可以推得第一个公式。第二个可以根据 ∂ C ∂ δ i L − 1 \frac{\partial C}{\partial \delta^{L-1}_{i}} ∂δiL−1∂C求得。
量化公式
量化指数

这个是用来衡量量化精度的。
核心量化公式
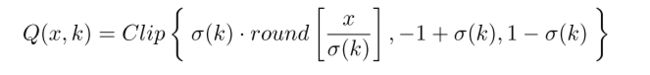
分析一下这个公式。第一项是指精度。将超出精度的位去掉。后面两项是量化的上下限。对于这个上下限,不清楚为什么这么设定。但这个设定保证了量化后的值在[-1,1]之间呈对称分布。
Stochastic Rounding
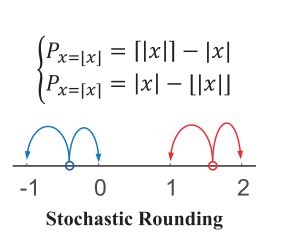
文章中的取整不是确定的,是依概率的。这种方法会带来额外的计算量
Shift

Shift函数的意思是将x归并到离他最近的2的幂次方上。至于为什么要做这样的的操作,作者给出了下面的解释

也就是如果不在量化之前做shift,量化值会出现严重的偏斜。可是并不理解这一点。
weight initialization

这套做法不是作者原创,来自另外一篇文章。需要再研究下。目前所知道的就是W的初始化与输入维度有关系。
quantization details
weight quantization
activation quantization


这个公式我的理解可能有些问题,在此做个记录,以便后续改正。
由weight initialization 公式可以得知: a = L m i n / L ∈ ( 0 , 1 ] a=L_{min}/L \in(0,1] a=Lmin/L∈(0,1] 那么 S h i f t ( a ) ∈ ( 0 , 1 ] Shift(a) \in (0,1] Shift(a)∈(0,1] 。所以 α \alpha α 始终为1. 那么做这个操作是为了什么呢?
正是这个scale操作加上之前的weight初始化操作使得本篇文章得以舍弃bn并且取得与bn类似的效果。这里不理解有点尴尬了。需要看看那篇介绍初始化的论文解决这个问题。
error quantization
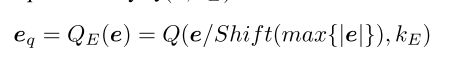
由于e的range非常大, [ 1 0 − 9 , 1 0 − 4 ] [10^{-9}, 10^{-4}] [10−9,10−4],那么这里量化的作用是保留与 m a x ( e ) max(e) max(e)量级相近的误差,将过于小的误差去掉。同时对于过大的误差,也做了规范。
gradient quantization

上面的公式的含义是将g扩大相应的倍数,使得其整数位有值;这么做的原因如下:
gradient量化之后,也就意味着 Δ W \Delta W ΔW有最小更新粒度,就是 σ ( k G \sigma (k_{G} σ(kG。因此在计算 Δ W \Delta W ΔW时,我们要给出 σ ( k G \sigma (k_{G} σ(kG的计数。
只是这样有一点无法对应,就是g扩大的倍数。max{|g|}的位数无法保证就是gradient保存的精度。所以我对下面的公式也无法理解

按照上面公式所说,(先去掉bernoulli项),无论 m a x ( g s ) max(g_{s}) max(gs)有多大,都会造成整数个 σ ( k G ) \sigma(k_{G}) σ(kG)的更新,这就让人比较费解。也许文中所说的只记录gradient的相对大小而不是绝对大小可以对应上面的问题。如果是这样,为什么不采用绝对大小呢?并不会造成太多的存储和计算上的变动,反而能够提高精度。
可能时我理解的有问题,在此做记录,以便日后修改
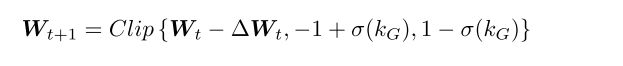
这个是更新公式
总结
本篇文章有几个亮点:
1:用合理的初始化和scale替代了BN,从而降低了对数据精度的要求
2:不同于post-training quantization或者training-aware quantization,本文所介绍的方法在training和inference时模型是一致的。
3:文章对weight,activation,gradient,error都做了量化,量化深度更深。
不足:
1:这篇文章是我看到的第一个彻底不使用bn的。他通过对weight合理的初始化和scale取代了bn操作。只是他这种做法还是比较粗糙。比如他把activation量化到 [ − 1 + σ ( k ) , 1 − σ ( k ) ] [-1+\sigma (k),1-\sigma (k)] [−1+σ(k),1−σ(k)]的对称区间,就认为activation的均值应该是0,从而只给出了一个scale操作代替bn。这是一个比较不合理的做法。另外初始化方式的效果也有待商榷。
