树链剖分详解

树链剖分定义

只是把一棵树拆成链来处理而已，即将树上的某些段一起通过数据结构优化进行处理来降低复杂度。

树链剖分相关定义

1. 重儿子： ve[v] 为 u 的子节点中 ve 值最大的，那么 v 就是 u 的重儿子(将子树中最长的那一条链一起处理来降低复杂度)。
2. 轻儿子： u 除了重儿子的其它子节点。
3. 重边：点 u 与其重儿子的连边。
4. 轻边：点 u 与其轻儿子的连边。
5. 重链：由重边连成的路径。
6. 轻链：轻边。

树链剖分基本性质

1. 如果 (v,u) 为轻边，则 ve[u]×2<ve[v] ;
2. 从根到某一点的路径上轻链、重链的个数都不大于 logn 。

树链剖分独特之处

主要针对路径进行处理，我们平时处理一颗树的路径的方案一般就是求解 LCA 的各类算法，在线ST，离线tarjan，以及LCA在线倍增法，其实LCA在线倍增法在求解路径方面已经颇为让人满意了， O(nlogn) 构建， O(logn) 进行查询，比如一般的求解路径上的最大边权，点权之类的一般LCA倍增法都可以解决，如果再离线一下，或许复杂度更低。

但是树链剖分的独特之处就是可以对路径进行修改，一般结合线段树进行处理，查询更新的复杂度就是 O(logn) ，这是LCA在线倍增所不能做到的。

树链剖分理解

拿求解一条路径上的最大值做例子，树链剖分的思想就是，先对路径进行预处理，将路径上的数据分为几段，然后再对这几段求最大值，有点像分桶法。

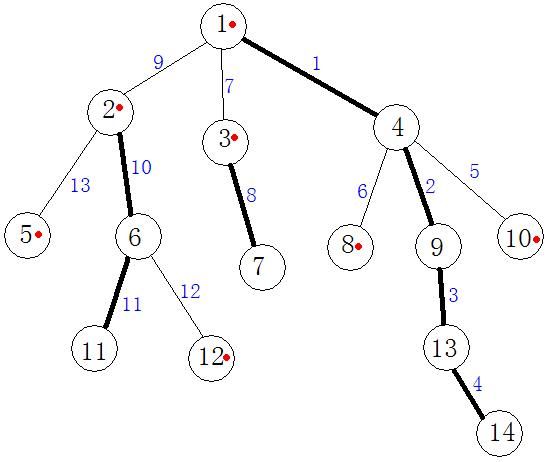
看下图：

比如我们要求解从顶点 11 到顶点 14 路径上边权的最大值，我们可以求出 1−4−9−13−14 这条路径上的最大值 s1 ，然后求出 1−2 路径上的最大值 s2 ,然后再求出 2−6−11 路径上的最大值 s3 。然后我们再求解 max(s1,s2,s3) 的值就可以得到结果 [ 黑色的路径表示图中黑色的路径，代表着重儿子，蓝色的则是代表着不是重儿子的路径 ]

从图上我们可以看出，重儿子所在的路径是子树中路径最长的，这也是为什么重儿子的定义是子树中节点最多的子节点，然后我们也发现黑色的路径上的蓝色编号是连续的，这是为了将这个长的路径保存在一段连续的区间，那么我就可以了对这块连续区间进行操作了。
也许大家已经想到了这样规定的好处，因为越长的，我就一起处理，效率自然是越高了，重儿子就是这么规定而来的。

然后我们对于区间求最值有很多方法，线段树一般就是最优的。

相关数组定义

deep[u]: 来保存当前节点 u 的深度

fa[u]: 用来保存当前节点 u 的父亲

ve[u]: 用来保存以 u 为根的子树节点个数

son[u]: 用来保存当前节点 u 的重儿子

top[u]: 用来保存当前节点 u 的所在链的顶端节点

p[u]: 用来保存当前节点 u 在线段树中的位置

fp[]: 用来保存线段树相应位置保存的是当前哪个节点

模板代码dfs1

void dfs1(int u, int pre, int d) {
    deep[u] = d;//深度
    fa[u] = pre;//父亲
    ve[u] = 1;//节点个数
    son[u] = -1;//重儿子
    for(int i = Head[u]; ~i; i = E[i].nxt) {
        int v = E[i].v;
        if(v == pre) continue;
        dfs1(v, u, d + 1);
        ve[u] += ve[v];
        if(son[u] == -1 || ve[v] > ve[son[u]]) {//得到重儿子
            son[u] = v;
        }
    }
}

第一个 dfs1 是为了找重边，记录下所有的重边以及相关关系

模板代码dfs2

void dfs2(int u, int sp) {
    top[u] = sp;
    p[u] = ++ sz;
    fp[p[u]] = u;
    if(son[u] == -1) return;
    dfs2(son[u], sp);
    for(int i = Head[u]; ~i; i = E[i].nxt) {
        int v = E[i].v;
        if(v == son[u] || v == fa[u]) continue;
        dfs2(v, v);
    }
}

第二个dfs2就是为了连接重边形成重链，即将这条长路径给连接起来，具体步骤：以根节点为起点，沿着重边向下拓展，拉成重链，不在当前重链上的节点，都以该节点为起点向下重新拉一条重链。

到此，树链剖分部分完毕，构造的每条重链相当于一段连续的区间，然后就是用数据结构处理数据 [ 一般是线段树处理 ] 。

如何沿着路径进行处理（以查找最大值为例）

步骤跟在求解 11 到 14 的最大值一样。

int find(int u, int v)  {
    int f1 = top[u], f2 = top[v];
    int tmp = 0;
    while(f1 != f2)  {
        if(deep[f1] < deep[f2])   {
            swap(f1, f2);
            swap(u, v);
        }
        tmp = max(tmp, query(1, p[f1], p[u]));
        u = fa[f1];
        f1 = top[u];
    }
    if(u == v)return tmp;
    if(deep[u] > deep[v]) swap(u, v);
    return max(tmp, query(1, p[son[u]], p[v]));
}

分析：

1. 如果u与v在同一条重链上，那么就直接修改了，因为他们是连续的
2. 如果不在一条重链上，则往一条重链上靠拢，然后就会编程一条重链

---

[ 有些地方不一定说得很清楚，希望大家指出，谢谢！ ]