数学基础（三）：凸优化对偶理论（拉格朗日对偶函数，主对问题，强弱对偶问题）

数学基础系列博客是自己在学习了稀牛学院&网易云课堂联合举办的《人工智能数学基础》微专业后的课程笔记总结。怀着对授课讲师Jason博士无限的敬佩与感激之情，我在完整听了两遍课程之后，对这门进行了笔记整理。Jason博士用深入浅出的方式把数学知识真的是讲透彻了，我的笔记显然无法完整传达Jason博士的精彩授课内容，在此非常推荐每一个打算进入或了解AI的同学去学习这门课程！

一：一般优化问题

$$\begin{gathered} minmize{f}_0(\mathbf{x}) \\ subjectto{f}_i(\mathbf{x})\le 0fori=1,2,...m \\ {h}_i(\mathbf{x})=0fori=1,2,...p \end{gathered}$$

问题的定义域$\mathcal{D}=\left({\bigcap }_{i=0}^m\mathrm{dom}{f}_i\right)\bigcap \left({\bigcap }_{i=0}^p\mathrm{dom}{h}_i\right)$.需要注意的是 ：定义域与可行域是不同的。可行域是同时满足目标函数定义域和约束条件的x的集合。

二：拉格朗日函数

2.1 函数基本介绍

• 拉格朗日函数将目标函数和约束条件整合到了一起。
  $$L(\mathbf{x},\lambda ,v)=f_0(\mathbf{x})+\sum _{i=1}^m{\lambda }_i{f}_i(\mathbf{x})+\sum _{i=1}^p{v}_i{h}_i(\mathbf{x})$$

• 主变量 ：$\mathbf{x}$

• 对偶变量：$\lambda \ge 0$,即$\lambda =[{\lambda }_1,{\lambda }_2,\cdots {\lambda }_m{]}^T\ge 0$;而$\mathbf{v}$可以大于等于0，也可以小于等于0.

• 意义解释：这其实是一种添加惩罚的方式。如果约束条件$f_i(\mathbf{x})\ge 0$,那么就相当于加了一个正数($\lambda \ge 0$)，使得拉格朗日函数变大，而我们的目标在于最小化该函数，因此就会强迫约束条件小于等于0。

2.2 函数的主问题分析

$$L(\mathbf{x},\lambda ,\mathbf{v})=f_0(\mathbf{x})+\sum _{i=1}^m{\lambda }_i{f}_i(\mathbf{x})+\sum _{i=1}^p{v}_i{h}_i(\mathbf{x})$$

• 主问题：
  $$p^{\ast }=\underset{\mathbf{x}}{\min }\{\underset{(\lambda ,v)}{\max }L(\mathbf{x},\lambda ,\mathbf{v}))\}$$

• 主问题分析：我们的目标其实是${\min }_{\mathbf{x}}{f}_0(\mathbf{x})$,即我们要求函数$f_0(\mathbf{x})$的最小值，而不是$maxL$的最小值。那么原函数和$maxL$之间有什么关系呢？

  我们单独看max的部分：
  $$\underset{\lambda ,v}{\max }L(\mathrm{x},\lambda ,v)=f_0(\mathrm{x})+\underset{\lambda ,v}{\max }\left(\sum _{i=1}^m{\lambda }_i{f}_i(\mathrm{x})+\sum _{i=1}^p{v}_i{h}_i(\mathrm{x})\right)$$
  在这个函数中，$\lambda$和$v$是变量。当x在可行域范围内时，$f_i(\mathbf{x})\le 0,\lambda \ge 0$,所以括号中第一项小于等于0；第二项中由于$h_i(\mathbf{x})=0$,所以第二项也为0。这样也就是说${\max }_{\lambda ,v}\left({\sum }_{i=1}^m{\lambda }_i{f}_i(\mathrm{x})+{\sum }_{i=1}^p{v}_i{h}_i(\mathrm{x})\right)$的值为0。所以最小化$maxL$和最小化目标函数是等效的。

2.3 函数的对偶问题分析

• 拉格朗日对偶函数
  $$g(\mathbf{\lambda },\mathbf{v})=\underset{\mathbf{x}\in \mathcal{D}}{\min }L(\mathbf{x},\mathbf{\lambda },\mathbf{v})=\underset{\mathbf{x}\in \mathcal{D}}{\min }\left\{f_0(\mathbf{x})+\sum _{i=1}^m{\lambda }_i{f}_i(\mathbf{x})+\sum _{i=1}^p{v}_i{h}_i(\mathbf{x})\right\}$$

  • 需要注意：这个对偶函数是定义在函数定义域上的，不是可行域。

  • 回忆：逐点最大：$f_1,\cdots ,f_m$凸，则$f(\mathrm{x})=\max \left\{f_1(\mathrm{x}),\cdots ,f_m(\mathrm{x})\right\}$ 凸。$f(\mathbf{x},\mathbf{y})$对于每个$\mathrm{y}\in \mathcal{A}$凸，则${\max }_{y\in \mathcal{A}}f(x,y)$凸。

  • $g(\mathbf{\lambda },\mathbf{v})$其实是关于$\lambda ,v$的仿射函数，所以是既凸且凹的函数。所以该函数的逐点下确界总是凹的。即$g(\mathbf{\lambda },\mathbf{v})$是一个凹函数。

  • 相当于，给定一个$\mathbf{x}$，然后大括号里面有很多个仿射函数，这些仿射函数的逐点下确界是凹函数。

  • 如果$\tilde{\mathbf{x}}$是一个可行域中的点，则：
    $$g(\mathbf{\lambda },\mathbf{v})=\underset{\mathbf{x}\in \mathcal{D}}{\min }L(\mathbf{x},\mathbf{\lambda },\mathbf{v})\le L(\mathbf{x},\mathbf{\lambda },\mathbf{v})$$

    • 因为$g(\mathbf{\lambda },\mathbf{v})$是拉格朗日函数在整个定义域上的的最小值，又因为可行域仅仅是定义域的一部分，所以它小于等于可行域中的任何一个函数值。

    • 又因为
      $$L(\mathbf{x},\mathbf{\lambda },\mathbf{v})=f_0(\mathbf{x})+\sum _{i=1}^m{\lambda }_i{f}_i(\mathbf{x})+\sum _{i=1}^p{v}_i{h}_i(\mathbf{x})\le f_0(\mathbf{x})$$

      • 因为对于可行域中的点，$f_i(\mathbf{x})\le 0$,$h_i(\mathbf{x})=0$.所以$L(\mathbf{x},\mathbf{\lambda },\mathbf{v})\le f_0(\mathbf{x})$.这也就是说$g(\mathbf{\lambda },\mathbf{v})\le f_0(\mathbf{x})$,即$g(\mathbf{\lambda },\mathbf{v})$小于等于$f_0(\mathbf{x})$中任意一点的函数值，当然也就小于其最小值了，即$g(\mathbf{\lambda },\mathbf{v})\le f_0({\mathbf{x}}^{\ast })=p^{\ast }$。

      • 从上边的分析中可以看出，对偶问题小于等于原问题最优解的下界。如果我们能够求出对偶问题的上界，那么就可以确定一个原问题的下界。接下来我们就想办法求对偶问题的上界，即最大值。

• 拉格朗日对偶问题：
  $$\begin{array}{ll}\text{ maximize }& g(\lambda ,v)\\ \text{ subject to }& \lambda \ge 0\end{array}$$

• 目标函数：${\max }_{\lambda \ge 0,\mathrm{v}}{\min }_{\mathrm{x}\in \mathcal{D}}L(\mathrm{x},\lambda ,v)$

• 这其实是一个凹函数在凸集上的最大化问题。是一个凸优化问题。设其最优值为$d^{\ast }$，对应的极值点为${\lambda }^{\ast },v^{\ast }$。

• 从以上分析中我们就可以得出一个结论：不管原问题是不是一个凸优化问题，他的对偶问题一定是一个凸优化问题。$g({\lambda }^{\ast },{\mathbf{v}}^{\ast })=d^{\ast }\le p^{\ast }$,即对偶问题的最大值小于等于原问题的最小值。

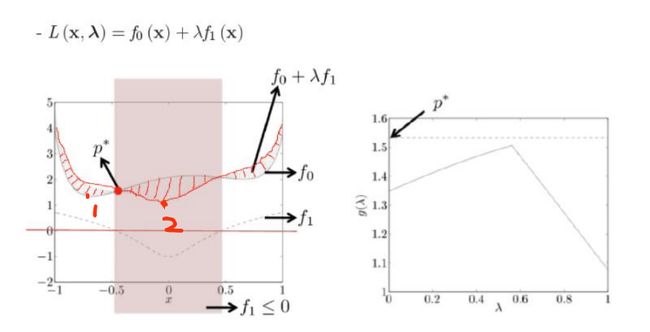
2.4 对偶问题的几何解释

• 可行域为图中阴影部分；定义域为[-1,1]
• 原问题的最小值（即可行域中的最小值）在$p^{\ast }$x处。
• 当$\lambda =0$时，$L(\mathbf{x},\lambda )=f_0(\mathbf{x})$.函数在定义域上的最小值在1处，约为1.3。当$\lambda =1$时，$L(\mathbf{x},\lambda )=f_0(\mathbf{x})+f_1(\mathbf{x})$,此时函数的最小值在2处，约为0.8.当$\lambda$在[0,1]之间变化时，对偶问题的最大值始终小于原函数的最小值（参考右边图）。
• 在整个定义域上，对偶问题的最大值小于等于原问题的最小值。

2.5 强弱对偶问题解释

• 弱对偶：$d^{\ast }<p^{\ast }$，无论原问题是不是凸优化问题，总成立

• 强对偶：$d^{\ast }=p^{\ast }$,

  • 该条件通常不成立

  • 但是对于凸优化问题通常成立

  • 凸优化问题可以改写为：
    $$\begin{gathered} minimize{f}_0(\mathbf{x}) \\ subjectto{f}_i(\mathbf{x})\le 0fori=1,2,\cdots m \\ \mathbf{A}\mathbf{x}=\mathbf{b} \end{gathered}$$

  • slater条件：存在内点$\mathbf{x}$。使得$f_i(\mathbf{x})<0fori=1,2,\cdots m$均成立。

• 说明：如果没有不等式约束，只有$\mathbf{A}\mathbf{x}=\mathbf{b}$，那么一定是强对偶；如果存在不等式约束，那么满足slater条件时，是强对偶；但是需要注意的是：不满足slater条件，不代表一定不是强对偶问题。

2.6 从对偶问题解主问题

• 假定强对偶问题成立，$\left({\mathrm{x}}^{\ast },{\lambda }^{\ast },v^{\ast }\right)$是主问题和对偶问题的最优解，那么
  $$\begin{array}{rl}{p}^{\ast }=f_0\left({\mathrm{x}}^{\ast }\right)& =d^{\ast }=g\left({\lambda }^{\ast },v^{\ast }\right)\\ & =\underset{\mathbf{x}}{\min }\left(f_0(\mathrm{x})+\sum _{i=1}^m{\lambda }_i^{\ast }{f}_i(\mathrm{x})+\sum _{i=1}^p{v}_i^{\ast }{h}_i(\mathrm{x})\right)\\ & \text{最小值肯定小于等于任意一个x对应的函数值，因此}\\ & \le f_0\left({\mathrm{x}}^{\ast }\right)+\sum _{i=1}^m{\lambda }_i^{\ast }{f}_i\left({\mathrm{x}}^{\ast }\right)+\sum _{i=1}^p{v}_i^{\ast }{h}_i\left({\mathrm{x}}^{\ast }\right)\\ & \text{因为x星肯定在函数的可行域内，因此后边两项均为非正值，因此}\\ & \le f_0\left({\mathrm{x}}^{\ast }\right)\end{array}$$

• 观察上式首尾两项，可得$f_0({\mathrm{x}}^{\ast })\le f_0({\mathrm{x}}^{\ast })$，因此小于等于号可变为等号。因此也就可以得到：

  • 结论1：${\lambda }_i^{\ast }{f}_i\left({\mathrm{x}}^{\ast }\right)=0$
  • 结论2：$L\left(\mathrm{x},{\lambda }^{\ast },v^{\ast }\right)$关于${\mathbf{x}}^{\ast }$处取极小值，有${\nabla }_{\mathrm{x}}L\left({\mathrm{x}}^{\ast },{\lambda }^{\ast },v^{\ast }\right)=0$
    • $g\left({\lambda }^{\ast },v^{\ast }\right)=L\left({\mathrm{x}}^{\ast },{\lambda }^{\ast },v^{\ast }\right)$；对偶函数的最优解就在拉格朗日函数取极值的时候
    • $g\left({\lambda }^{\ast },v^{\ast }\right)={\min }_{x}L\left(\mathrm{x},{\lambda }^{\ast },v^{\ast }\right)$

2.7 KKT条件

• 凸优化问题：
  $$\begin{gathered} minmize{f}_0(\mathbf{x}) \\ subjectto{f}_i(\mathbf{x})\le 0fori=1,2,...m \\ {h}_i(\mathbf{x})=0fori=1,2,...p \end{gathered}$$

• 拉格朗日函数
  $$L(\mathrm{x},\lambda ,v)=f_0(\mathrm{x})+\sum _{i=1}^m{\lambda }_i{f}_i(\mathrm{x})+\sum _{i=1}^p{v}_i{h}_i(\mathrm{x})$$

• 凸优化问题强对偶成立的充要条件：

  • $f_i\left({\mathrm{x}}^{\ast }\right)\le 0,i=1,\cdots ,m\left({\nabla }_{\lambda }L\left({\mathrm{x}}^{\ast },\lambda ,v\right)\le 0\right)$
  • $h_i\left({\mathrm{x}}^{\ast }\right)=0,i=1,\cdots ,p\left({\nabla }_{\mathrm{v}}L\left({\mathrm{x}}^{\ast },\lambda ,v\right)=0\right)$
  • ${\lambda }_i^{\ast }\ge 0,i=1,\cdots ,m$
  • ${\lambda }_i^{\ast }{f}_i\left({\mathrm{x}}^{\ast }\right)=0,i=1,\cdots ,m$
  • $\nabla f_0\left({\mathrm{x}}^{\ast }\right)+{\sum }_i{\lambda }_i^{\ast }\nabla f_i\left({\mathrm{x}}^{\ast }\right)+{\sum }_i{v}_i^{\ast }\nabla h_i\left({\mathrm{x}}^{\ast }\right)=0\left({\nabla }_{\mathrm{x}}L\left({\mathrm{x}}^{\ast },{\lambda }^{\ast },v^{\ast }\right)=0\right)$

• KKT问题的几何解释（知乎解释）：https://www.zhihu.com/question/58584814/answer/159863739.

2.8 主对问题思考

• 主问题：
  $$p^{\ast }=\underset{\mathbf{x}}{\min }\left(\underset{\lambda \ge 0,v}{\max }L(\mathbf{x},\mathbf{\lambda },\mathbf{v})\right)$$

• 对偶问题
  $$d^{\ast }=\underset{\lambda \ge 0,\mathrm{v}}{\max }\left(\underset{\mathbf{x}}{\min }L(\mathbf{x},\mathbf{\lambda },\mathbf{v})\right)$$

• 主对关系（强对偶成立时，max和min可以互换，即可以取等号）
  $$\underset{\lambda \ge 0,\mathrm{v}}{\max }\left(\underset{\mathbf{x}}{\min }L(\mathbf{x},\mathbf{\lambda },\mathbf{v})\right)\le \underset{\mathbf{x}}{\min }\left(\underset{\mathbf{\lambda }\ge 0,\mathbf{v}}{\max }L(\mathbf{x},\mathbf{\lambda },\mathbf{v})\right)$$

三：具体计算案例

3.1最小二范数问题

• 求解下列问题

$$\begin{array}{c}{p}^{\ast }={\min }_{\mathbf{x}}\Vert \mathbf{x}{\Vert }_2^2\\ \text{ s.t. }\mathbf{A}\mathbf{x}=\mathbf{b}\end{array}$$

分析一下问题：首先目标函数是一个二范数，可以看作${\mathbf{x}}^{\mathbf{T}}\mathbf{I}\mathbf{x}$，其中$\mathbf{I}$为正定矩阵。所以是一个凸函数。另外，约束条件为等式约束，是超平面的集合，是凸集。因此问题是一个凸优化问题。

解法：

1. 写出拉格朗日函数：
   $$L(\mathrm{x},\mathrm{v})={\mathrm{x}}^T\mathrm{x}+{\mathrm{v}}^T(\mathrm{A}\mathrm{x}-\mathrm{b})$$

2. 写出对偶函数：
   $$g(\mathbf{v})=\underset{\mathbf{x}}{\min }L(\mathbf{x},\mathbf{v})$$

则：
$$\begin{array}{l}{\nabla }_{\mathbf{x}}L(\mathbf{x},\mathbf{v})=0\Rightarrow 2\mathbf{x}+{\mathbf{A}}^T\mathbf{v}=0\Rightarrow {\mathbf{x}}^{\ast }(\mathbf{v})=-\frac{1}{2}{\mathbf{A}}^T\mathbf{v}\\ g(\mathbf{v})=L\left({\mathbf{x}}^{\ast }(\mathbf{v}),\mathbf{v}\right)=-\frac{1}{4}{\mathbf{v}}^T\left(\mathbf{A}{\mathbf{A}}^T\right)\mathbf{v}-{\mathbf{v}}^T\mathbf{b}\end{array}$$
g(v)是一个凹函数

3. 对偶问题：
   $$d^{\ast }=\underset{\mathbf{v}}{\max }-\frac{1}{4}{\mathbf{v}}^T\left(\mathbf{A}{\mathbf{A}}^T\right)\mathbf{v}-{\mathbf{v}}^T\mathbf{b}$$

可求得：
$$\begin{array}{rl}\mathbf{v}\ast & =-2{\left(\mathbf{A}{\mathbf{A}}^T\right)}^{-1}\mathbf{b}\\ d^{\ast }& ={\mathbf{b}}^T{\left(\mathbf{A}{\mathbf{A}}^T\right)}^{-1}\mathbf{b}\end{array}$$
由于$p^{\ast }=d^{\ast }$,则
$${\mathbf{x}}^{\ast }={\mathbf{x}}^{\ast }\left({\mathbf{v}}^{\ast }\right)={\mathbf{A}}^T{\left(\mathbf{A}{\mathbf{A}}^T\right)}^{-1}\mathbf{b}$$

$$p^{\ast }\ge -\frac{1}{4}{\mathbf{v}}^T\left(\mathbf{A}{\mathbf{A}}^T\right)\mathbf{v}-{\mathbf{v}}^T\mathbf{b}\text{ for all }\mathbf{v}$$

四：参考资料

1. https://www.zhihu.com/question/58584814/answer/159863739
2. 网易云课堂《人工智能数学基础》