- LabVIEW MathScript薄板热流模拟
LabVIEW开发
LabVIEW参考程序LabVIEW知识LabVIEW知识LabVIEW程序LabVIEW功能labview
热流模拟是热设计关键环节,传统工具精准但开发周期长,本VI利用LabVIEW优势,面向工程师快速验证需求,在初步方案迭代、教学演示等场景更具效率,为热分析提供轻量化替代路径,后续可结合专业工具,先通过本VI快速定性分析,再用传统工具精准求解,提升研发流程效率。此VI用于模拟单点热源下薄板的热流,求解带周期边界条件的椭圆型偏微分方程,借助LabVIEWMathScriptNode实现自定义函数,结合
- 人形机器人运动控制技术演进:从强化学习到神经微分方程的前沿解析
1.引言:人形运动控制的挑战与范式迁移人形机器人需在非结构化环境中实现双足行走、跑步、跳跃等复杂动作,其核心问题可归结为高维连续状态-动作空间的实时优化。传统方法(如基于模型的预测控制MPC)依赖精确的动力学建模,但在实际系统中面临以下瓶颈:模型失配:复杂接触动力学(如足-地交互)难以显式建模;计算瓶颈:高维非线性优化难以满足实时性需求;环境扰动敏感:传统控制器对未知干扰的鲁棒性不足。近年来,以强
- MIT 6.S184 Lec01 Flow and Diffusion Models
克斯维尔的明天_
机器学习人工智能
MIT6.S184Lec01FlowandDiffusionModels本节中,我们将描述如何通过模拟一个适当构造的微分方程来获得所需的转换。例如,流匹配和扩散模型分别涉及模拟常微分方程(ODE)和随机微分方程(SDE)。因此,本节的目标是定义和构建这些生成模型。具体来说,我们首先定义ODE和SDE,并讨论它们的模拟。其次,我们描述如何使用深度神经网络对ODE/SDE进行参数化。从中推导出流模型和
- 求解偏微分方程的Fourier展开式
解答:(1)求解的Fourier展开式考虑边值问题:∂2u∂t2=∂∂x((cosx+2)∂u∂x)−(sinπxl)u,(x,t)∈(0,l)×(0,T),\frac{\partial^2u}{\partialt^2}=\frac{\partial}{\partialx}\left((\cosx+2)\frac{\partialu}{\partialx}\right)-\left(\sin\
- 2023考研数一真题及答案
猿六凯
考研
历年数一真题及答案下载直通车曲线y=xln(e+1x−1)y=x\ln(e+\frac{1}{x-1})y=xln(e+x−11)的渐近线方程为()(A)y=x+ey=x+ey=x+e(B)y=x+1ey=x+\frac{1}{e}y=x+e1©y=xy=xy=x(D)y=x−1ey=x-\frac{1}{e}y=x−e1若微分方程y′′+ay′+by=0y''+ay'+by=0y′′+ay′+
- 云计算在可视化非线性偏微分方程动力学中的应用:拟线性和半线性示例-AI云计算数值分析和代码验证
亚图跨际
AI云计算人工智能
“拟线性”和“半线性”代表了非线性偏微分方程(PDEs)这一大类中的重要分类。其区别主要在于非线性的表现形式,特别是与未知函数的最高阶导数之间的关系。在偏微分方程的研究中,将其分为线性、半线性、拟线性和完全非线性至关重要,因为用于分析和求解它们(例如,解的存在性、唯一性、正则性、数值方法)的数学技术根据其线性性质而显著不同。非线性偏微分方程通常比线性偏微分方程更难求解和分析,即使在非线性类别中,由
- 模拟多维物理过程与基于云的数值分析-AI云计算数值分析和代码验证
亚图跨际
AI人工智能云计算
高维输运与扩散方程,涵盖了严格的扩散极限、多维扩散理论、先进的数值和基于粒子的模拟方法,以及分数阶/电报式推广,为广泛的科学和工程领域中复杂输运现象的建模、分析和模拟提供了强大的工具。高维输运和扩散方程涵盖了输运方程的严格扩散极限、结合随机和偏微分方程工具的多维扩散理论、先进的数值和基于粒子的模拟方法、分数阶和电报式输运的推广,以及在地球物理和工程系统中的应用。这些框架为建模、分析和模拟许多科学和
- 《高等数学》(同济大学·第7版)第十二章 无穷级数 第五节函数的幂级数展开式的应用
没有女朋友的程序员
高等数学
一、幂级数展开的核心作用幂级数展开不仅是理论工具,更是解决实际问题的计算利器,主要应用包括:近似计算:用多项式逼近复杂函数(如计算函数值、积分值)。求解微分方程:将解表示为幂级数形式,逐项代入方程求解。求和与积分:将难以处理的级数转化为已知函数的展开式。分析函数性质:通过展开式研究函数的极值、拐点等。二、典型应用详解近似计算函数值原理:用泰勒多项式的前几项近似代替原函数。关键步骤:写出函数的麦克劳
- 《高等数学》(同济大学·第7版)第七章 微分方程 第四节一阶线性微分方程
没有女朋友的程序员
高等数学
好的,这是将您提供的高等数学教案内容中的LaTeX公式转换为纯文本格式后的版本:同学们好!今天我们学习《高等数学》第七章第四节“一阶线性微分方程”。这是一阶微分方程中最重要、应用最广泛的一类方程,掌握它的解法对后续学习(如微分方程的应用、高阶线性微分方程)至关重要。我会用最通俗的语言,结合大量例子,帮你彻底掌握“一阶线性微分方程”的定义、解法和核心思想。一、一阶线性微分方程的定义:长什么样?1.标
- 蔡高厅老师 - 高等数学-阅读笔记 - 01 - 前言、函数【视频第01、02、03、】
Franklin
数学线性代数
高等数学前言;196学时,每周6课主要内容:上册一元、多元函数数,微分学、积分学、矢量代数、空间解析几何无穷级数、微分方程,多元函数微分学和积分学目的:高等数学3基:1高等数学的基本知识2高度数学的基本理论3高等数学的基本计算方法提高数学素养培养:抽象思维、逻辑推理、辩证的思想方法、空间想象能力、分析问题、解决问题的能力为进一步学习打下必要的学习基础和初等数学不同,研究的不是常量而是变量,变量和变
- 高等数学》(同济大学·第7版)第七章 微分方程 第五节可降阶的高阶微分方程
没有女朋友的程序员
高等数学
好的,这是将您提供的高等数学第七章第五节教案内容中的LaTeX公式转换为纯文本格式后的版本:同学们好!今天我们学习《高等数学》第七章第五节“可降阶的高阶微分方程”。高阶微分方程(如二阶、三阶)直接求解困难,但许多方程可以通过“降阶”转化为低阶方程(如一阶方程)来求解。本节重点讲解三类可降阶的高阶微分方程,掌握它们的解法对后续学习至关重要。我会用最通俗的语言,结合大量例子,帮你彻底掌握。一、可降阶高
- 高等数学》(同济大学·第7版)第七章 微分方程 第三节齐次方程
没有女朋友的程序员
高等数学
同学们好!今天我们学习《高等数学》第七章第三节“齐次方程”。这是微分方程中一类重要的可转化方程,掌握它的解法对后续学习(如线性微分方程)有重要意义。我会用最通俗的语言,结合大量例子,帮你彻底掌握“齐次方程”的定义、特点和解法。一、齐次方程的定义:什么是“齐次”?1.齐次方程的两种含义在微积分中,“齐次”有两种常见含义,但这里我们特指一阶微分方程中的齐次方程:若一阶微分方程可以写成以下形式:dydx
- 线性代数和c语言先学哪个,线性代数和哪个更有用?
段丞博
线性代数和c语言先学哪个
一、从数学与应用数学这个专业来分析下“线性代数”和“高等数学”这两块的内容,无论哪块知识在“考研究生数学科目中的考试”都会涉汲到的,而且有些专业的考试也包括概率论与数理统计这块知识。线性代数和哪个更有用?1、线性代数内容:行列式、矩阵、向量、线性方程组、特征值和特征向量、二次型。2、高等数学内容:函数·极限·连续、导数与微分、不定积分、定积分及广义积分、中值定理的证明、常微分方程、一元微积分的应用
- 结构力学数值方法:谐波平衡法:高级谐波平衡法技术_2024-08-05_22-46-19.Tex
chenjj4003
材料力学2算法线性代数矩阵决策树人工智能
结构力学数值方法:谐波平衡法:高级谐波平衡法技术绪论谐波平衡法简介谐波平衡法(HarmonicBalanceMethod,HBM)是一种用于求解非线性振动系统周期解的数值方法。它通过将系统的响应表示为一系列谐波函数的线性组合,然后利用傅里叶级数展开,将非线性微分方程转换为一组代数方程,从而简化了求解过程。这种方法特别适用于分析具有周期性激励的非线性系统,如机械振动、电路振荡等。高级谐波平衡法技术的
- Flux Reconstruction(FR,通量重构)方法
东北豆子哥
重构算法人工智能
文章目录FluxReconstruction(FR,通量重构)方法**核心思想****关键步骤****优势****文献推荐****注意事项**FluxReconstruction(FR,通量重构)方法FluxReconstruction(FR,通量重构)方法是一种高阶精度的数值计算框架,主要用于求解偏微分方程(尤其是双曲守恒律方程),在计算流体力学(CFD)等领域有广泛应用。它结合了间断有限元法(
- python scipy简介
凤枭香
Python图像处理pythonscipy开发语言图像处理
scipyscipy是一个python开源的数学计算库,可以应用于数学、科学以及工程领域,它是基于numpy的科学计算库。主要包含了统计学、最优化、线性代数、积分、傅里叶变换、信号处理和图像处理以及常微分方程的求解以及其他科学工程中所用到的计算。scipy模块介绍scipy主要通过下面这些包来实现数学算法和科学计算,后面对于scipy的讲解主要也是基于这些包来实现的cluster:包含聚类算法co
- Python之scipy(算法/数学工具)用法
薛毅轩
python
scipy是一个开源的Python算法库和数学工具包,它基于NumPy,提供了许多用于数学、科学和工程的算法。scipy包含了统计、优化、积分、插值、特殊函数、快速傅里叶变换、信号处理、图像处理、常微分方程求解等模块。以下是一些scipy库的基本用法示例:1.特殊函数scipy.special模块提供了许多数学上的特殊函数。fromscipyimportspecial#计算阶乘和组合数factor
- 偏微分方程通解与初值问题求解2
weixin_30777913
算法
题目问题1.(a)求下列各方程的通解:ut+3ux−2uy=0;ut+xux+yuy=0;ut+xux−yuy=0;ut+yux+xuy=0;ut+yux−xuy=0.u_t+3u_x-2u_y=0;\quadu_t+xu_x+yu_y=0;\\u_t+xu_x-yu_y=0;\quadu_t+yu_x+xu_y=0;\\u_t+yu_x-xu_y=0.ut+3ux−2uy=0;ut+xux+yu
- [ 常微分方程 ] 01 ODE积分曲线和方向场可视化(Python)
有梦想的西瓜
数学python
今天老师布置了个一阶线性微分方程的python可视化作业,由于作者本人水平有限(爆哭),之后再把非线性和高阶微分方程学会了再一并补充进来。文章目录一阶微分方程一阶线性微分方程基本概念积分曲线:方向场图:等倾斜线图:例子1:dydx=x2−y\frac{dy}{dx}=x^2-ydxdy=x2−y例子2:dydx=x−y\frac{dy}{dx}=x-ydxdy=x−y一阶微分方程一阶线性微分方程基
- matlab求解常微分方程的实验,实验五 - - 用matlab求解常微分方程
胡千山
实验五用matlab求解常微分方程1.微分方程的概念未知的函数以及它的某些阶的导数连同自变量都由一已知方程联系在一起的方程称为微分方程。如果未知函数是一元函数,称为常微分方程。常微分方程的一般形式为F(t,y,y',y\,?,y(n))?0如果未知函数是多元函数,成为偏微分方程。联系一些未知函数的一组微分方程组称为微分方程组。微分方程中出现的未知函数的导数的最高阶解数称为微分方程的阶。若方程中未知
- matlab方程求解的实验,实验七用matlab求解常微分方程
蔡振原
matlab方程求解的实验
《实验七用matlab求解常微分方程》由会员分享,可在线阅读,更多相关《实验七用matlab求解常微分方程(7页珍藏版)》请在人人文库网上搜索。1、实验七用matlab求解常微分方程一、实验目的:1、熟悉常微分方程的求解方法,了解状态方程的概念;2、能熟练使用dsolve函数求常微分方程(组)的解析解;3、能熟练应用ode45ode15s函数分别求常微分方程的非刚性、刚性的数值解;4、掌握绘制相图
- 基于云计算的振动弦分析:谐波可视化与波动方程参数理解-AI云计算数值分析和代码验证
亚图跨际
AI云计算人工智能
振动弦方程是一个基础的偏微分方程,它描述了弹性弦的横向振动。其应用范围广泛,不仅可用于模拟乐器和一般的波动现象,更是数学物理以及深奥的弦理论中的重要基石。☁️AI云计算数值分析和代码验证振动弦方程是描述固定两端弹性弦横向振动的基本偏微分方程(PDE),其典型表达式为:∂2u∂t2=c2∂2u∂x2\frac{\partial^2u}{\partialt^2}=c^2\frac{\partial^2
- Python实例题:使用Python 解数学方程
狐凄
实例python开发语言
目录Python实例题题目1.解代数方程(如一元二次方程)2.使用SymPy解符号方程3.使用NumPy解线性方程组4.使用SciPy解非线性方程5.解微分方程总结Python实例题题目使用Python解数学方程1.解代数方程(如一元二次方程)对于简单的代数方程,可以直接使用求根公式:importmathdefsolve_quadratic(a,b,c):"""解一元二次方程ax²+bx+c=0"
- 《高等数学 第7版(同济大学 上册).pdf》资源介绍
孟津葵Gilda
《高等数学第7版(同济大学上册).pdf》资源介绍【下载地址】高等数学第7版同济大学上册.pdf资源介绍本资源提供《高等数学第7版(同济大学上册)》电子书,内容涵盖函数与极限、导数与微分、微分方程等核心章节,适合工科和理科学生系统学习。书中包含详细的理论讲解、丰富实例及习题答案,帮助读者深入理解高等数学知识。章节划分清晰,便于查找和学习。资源仅供学习研究使用,请合理利用,尊重知识产权。项目地址:h
- 振动力学:弹性杆的纵向振动(固有振动和固有频率的概念)
Wang的王
经典力学笔记笔记
文章1、2、3中讨论的是离散系统的振动特性,然而实际系统的惯性质量、弹性、阻尼等特性都是连续分布的,因而成为连续系统或分布参数系统。确定连续介质中无数个点的运动需要无限个广义坐标,因此也称为无限自由度系统,典型的结构例如:弦、杆、膜、环、梁、板、壳等,也称为弹性体。弹性体的微振动通常由偏微分方程描述。本文研究弹性杆的纵向振动特性。1.弹性杆纵向振动方程1.1振动方程某一直杆长为lll,沿杆件的轴线
- COMSOL Multiphysics软件二次开发:COMSOL软件在固体力学中的应用
kkchenjj
仿真模拟工业软件仿真模拟工业软件二次开发开发语言
COMSOLMultiphysics软件二次开发:COMSOL软件在固体力学中的应用COMSOLMultiphysics概述COMSOLMultiphysics是一款强大的多物理场仿真软件,它允许用户通过数值方法求解偏微分方程,从而模拟各种物理现象。软件的核心功能在于其灵活的建模环境和多物理场耦合能力,使得用户能够在一个统一的界面下,对涉及多种物理场的复杂问题进行仿真和分析。特点与应用多物理场耦合
- MATLAB实战:传染病模型仿真实现
三三十二
matlab开发语言
以下是一个使用MATLAB实现传染病模型(SIR和SEIR)仿真的完整解决方案,包含参数分析和干预措施模拟:%%传染病模型仿真工具箱%包含SIR、SEIR模型,支持参数调整和干预措施模拟%使用ode45求解微分方程functionepidemic_modeling()%主控制界面fig=uifigure('Name','传染病模型仿真','Position',[100100800600]);%模型
- 二阶线性微分方程的通解与特解
debug_running_Hu
线性代数算法机器学习学习
二阶线性微分方程的通解与特解二阶线性微分方程的一般形式为:a(x)y′′+b(x)y′+c(x)y=f(x)a(x)y''+b(x)y'+c(x)y=f(x)a(x)y′′+b(x)y′+c(x)y=f(x)其中,a(x),b(x),c(x)为系数函数,f(x)为非齐次项。1.齐次方程(f(x)=0):当f(x)=0时,方程变为齐次方程:a(x)y′′+b(x)y′+c(x)y=0a(x)y''+
- 泛函分析基础11-线性算子的谱1:谱的概念
u013250861
泛函分析基础泛函分析
谱论是泛函分析的重要分支之一.线性代数告诉我们:有限维空间上的线性算子由它的特征值和最小多项式完全确定.将这一结论推广到有界线性算子的情况,研究它的结构,就是算子的谱理论所谓算子的"谱",类似于有限维空间上算子—一矩阵的特征值.而无限维空间上的算子谱论,也就相当于把矩阵化为若尔当标准形.由于特征值和逆算子有密切关系,谱论也大量涉及逆算子的问题.将算子求逆应用到微分算子和积分算子上,推动了微分方程和
- matlab解高阶非齐次方程并作图,2x2齐次线性方程组作图
阿橘要努力上清华
主题:不同于一般常微分方程课程千篇一律地从分离变量和一阶线性方程讲起,MIT《微分方程》第一讲就以独特的视角从全局的角度诠释了微分方程的内涵。课程从方向场和积分曲线入手,深入透彻地剖析了微分方程的实质。一上来,撇开那些有解的特殊的微分方程不谈,却从几何方向通俗易懂,而又全面深入地告诉我们什么是微分方程,解微分方程其实是什么。主题:老头爽约了,他没有按之前说的,讲线性方程的解法,而是开始讲数值方法。
- java线程Thread和Runnable区别和联系
zx_code
javajvmthread多线程Runnable
我们都晓得java实现线程2种方式,一个是继承Thread,另一个是实现Runnable。
模拟窗口买票,第一例子继承thread,代码如下
package thread;
public class ThreadTest {
public static void main(String[] args) {
Thread1 t1 = new Thread1(
- 【转】JSON与XML的区别比较
丁_新
jsonxml
1.定义介绍
(1).XML定义
扩展标记语言 (Extensible Markup Language, XML) ,用于标记电子文件使其具有结构性的标记语言,可以用来标记数据、定义数据类型,是一种允许用户对自己的标记语言进行定义的源语言。 XML使用DTD(document type definition)文档类型定义来组织数据;格式统一,跨平台和语言,早已成为业界公认的标准。
XML是标
- c++ 实现五种基础的排序算法
CrazyMizzz
C++c算法
#include<iostream>
using namespace std;
//辅助函数,交换两数之值
template<class T>
void mySwap(T &x, T &y){
T temp = x;
x = y;
y = temp;
}
const int size = 10;
//一、用直接插入排
- 我的软件
麦田的设计者
我的软件音乐类娱乐放松
这是我写的一款app软件,耗时三个月,是一个根据央视节目开门大吉改变的,提供音调,猜歌曲名。1、手机拥有者在android手机市场下载本APP,同意权限,安装到手机上。2、游客初次进入时会有引导页面提醒用户注册。(同时软件自动播放背景音乐)。3、用户登录到主页后,会有五个模块。a、点击不胫而走,用户得到开门大吉首页部分新闻,点击进入有新闻详情。b、
- linux awk命令详解
被触发
linux awk
awk是行处理器: 相比较屏幕处理的优点,在处理庞大文件时不会出现内存溢出或是处理缓慢的问题,通常用来格式化文本信息
awk处理过程: 依次对每一行进行处理,然后输出
awk命令形式:
awk [-F|-f|-v] ‘BEGIN{} //{command1; command2} END{}’ file
[-F|-f|-v]大参数,-F指定分隔符,-f调用脚本,-v定义变量 var=val
- 各种语言比较
_wy_
编程语言
Java Ruby PHP 擅长领域
- oracle 中数据类型为clob的编辑
知了ing
oracle clob
public void updateKpiStatus(String kpiStatus,String taskId){
Connection dbc=null;
Statement stmt=null;
PreparedStatement ps=null;
try {
dbc = new DBConn().getNewConnection();
//stmt = db
- 分布式服务框架 Zookeeper -- 管理分布式环境中的数据
矮蛋蛋
zookeeper
原文地址:
http://www.ibm.com/developerworks/cn/opensource/os-cn-zookeeper/
安装和配置详解
本文介绍的 Zookeeper 是以 3.2.2 这个稳定版本为基础,最新的版本可以通过官网 http://hadoop.apache.org/zookeeper/来获取,Zookeeper 的安装非常简单,下面将从单机模式和集群模式两
- tomcat数据源
alafqq
tomcat
数据库
JNDI(Java Naming and Directory Interface,Java命名和目录接口)是一组在Java应用中访问命名和目录服务的API。
没有使用JNDI时我用要这样连接数据库:
03. Class.forName("com.mysql.jdbc.Driver");
04. conn
- 遍历的方法
百合不是茶
遍历
遍历
在java的泛
- linux查看硬件信息的命令
bijian1013
linux
linux查看硬件信息的命令
一.查看CPU:
cat /proc/cpuinfo
二.查看内存:
free
三.查看硬盘:
df
linux下查看硬件信息
1、lspci 列出所有PCI 设备;
lspci - list all PCI devices:列出机器中的PCI设备(声卡、显卡、Modem、网卡、USB、主板集成设备也能
- java常见的ClassNotFoundException
bijian1013
java
1.java.lang.ClassNotFoundException: org.apache.commons.logging.LogFactory 添加包common-logging.jar2.java.lang.ClassNotFoundException: javax.transaction.Synchronization
- 【Gson五】日期对象的序列化和反序列化
bit1129
反序列化
对日期类型的数据进行序列化和反序列化时,需要考虑如下问题:
1. 序列化时,Date对象序列化的字符串日期格式如何
2. 反序列化时,把日期字符串序列化为Date对象,也需要考虑日期格式问题
3. Date A -> str -> Date B,A和B对象是否equals
默认序列化和反序列化
import com
- 【Spark八十六】Spark Streaming之DStream vs. InputDStream
bit1129
Stream
1. DStream的类说明文档:
/**
* A Discretized Stream (DStream), the basic abstraction in Spark Streaming, is a continuous
* sequence of RDDs (of the same type) representing a continuous st
- 通过nginx获取header信息
ronin47
nginx header
1. 提取整个的Cookies内容到一个变量,然后可以在需要时引用,比如记录到日志里面,
if ( $http_cookie ~* "(.*)$") {
set $all_cookie $1;
}
变量$all_cookie就获得了cookie的值,可以用于运算了
- java-65.输入数字n,按顺序输出从1最大的n位10进制数。比如输入3,则输出1、2、3一直到最大的3位数即999
bylijinnan
java
参考了网上的http://blog.csdn.net/peasking_dd/article/details/6342984
写了个java版的:
public class Print_1_To_NDigit {
/**
* Q65.输入数字n,按顺序输出从1最大的n位10进制数。比如输入3,则输出1、2、3一直到最大的3位数即999
* 1.使用字符串
- Netty源码学习-ReplayingDecoder
bylijinnan
javanetty
ReplayingDecoder是FrameDecoder的子类,不熟悉FrameDecoder的,可以先看看
http://bylijinnan.iteye.com/blog/1982618
API说,ReplayingDecoder简化了操作,比如:
FrameDecoder在decode时,需要判断数据是否接收完全:
public class IntegerH
- js特殊字符过滤
cngolon
js特殊字符js特殊字符过滤
1.js中用正则表达式 过滤特殊字符, 校验所有输入域是否含有特殊符号function stripscript(s) { var pattern = new RegExp("[`~!@#$^&*()=|{}':;',\\[\\].<>/?~!@#¥……&*()——|{}【】‘;:”“'。,、?]"
- hibernate使用sql查询
ctrain
Hibernate
import java.util.Iterator;
import java.util.List;
import java.util.Map;
import org.hibernate.Hibernate;
import org.hibernate.SQLQuery;
import org.hibernate.Session;
import org.hibernate.Transa
- linux shell脚本中切换用户执行命令方法
daizj
linuxshell命令切换用户
经常在写shell脚本时,会碰到要以另外一个用户来执行相关命令,其方法简单记下:
1、执行单个命令:su - user -c "command"
如:下面命令是以test用户在/data目录下创建test123目录
[root@slave19 /data]# su - test -c "mkdir /data/test123"
- 好的代码里只要一个 return 语句
dcj3sjt126com
return
别再这样写了:public boolean foo() { if (true) { return true; } else { return false;
- Android动画效果学习
dcj3sjt126com
android
1、透明动画效果
方法一:代码实现
public View onCreateView(LayoutInflater inflater, ViewGroup container, Bundle savedInstanceState)
{
View rootView = inflater.inflate(R.layout.fragment_main, container, fals
- linux复习笔记之bash shell (4)管道命令
eksliang
linux管道命令汇总linux管道命令linux常用管道命令
转载请出自出处:
http://eksliang.iteye.com/blog/2105461
bash命令执行的完毕以后,通常这个命令都会有返回结果,怎么对这个返回的结果做一些操作呢?那就得用管道命令‘|’。
上面那段话,简单说了下管道命令的作用,那什么事管道命令呢?
答:非常的经典的一句话,记住了,何为管
- Android系统中自定义按键的短按、双击、长按事件
gqdy365
android
在项目中碰到这样的问题:
由于系统中的按键在底层做了重新定义或者新增了按键,此时需要在APP层对按键事件(keyevent)做分解处理,模拟Android系统做法,把keyevent分解成:
1、单击事件:就是普通key的单击;
2、双击事件:500ms内同一按键单击两次;
3、长按事件:同一按键长按超过1000ms(系统中长按事件为500ms);
4、组合按键:两个以上按键同时按住;
- asp.net获取站点根目录下子目录的名称
hvt
.netC#asp.nethovertreeWeb Forms
使用Visual Studio建立一个.aspx文件(Web Forms),例如hovertree.aspx,在页面上加入一个ListBox代码如下:
<asp:ListBox runat="server" ID="lbKeleyiFolder" />
那么在页面上显示根目录子文件夹的代码如下:
string[] m_sub
- Eclipse程序员要掌握的常用快捷键
justjavac
javaeclipse快捷键ide
判断一个人的编程水平,就看他用键盘多,还是鼠标多。用键盘一是为了输入代码(当然了,也包括注释),再有就是熟练使用快捷键。 曾有人在豆瓣评
《卓有成效的程序员》:“人有多大懒,才有多大闲”。之前我整理了一个
程序员图书列表,目的也就是通过读书,让程序员变懒。 写道 程序员作为特殊的群体,有的人可以这么懒,懒到事情都交给机器去做,而有的人又可
- c++编程随记
lx.asymmetric
C++笔记
为了字体更好看,改变了格式……
&&运算符:
#include<iostream>
using namespace std;
int main(){
int a=-1,b=4,k;
k=(++a<0)&&!(b--
- linux标准IO缓冲机制研究
音频数据
linux
一、什么是缓存I/O(Buffered I/O)缓存I/O又被称作标准I/O,大多数文件系统默认I/O操作都是缓存I/O。在Linux的缓存I/O机制中,操作系统会将I/O的数据缓存在文件系统的页缓存(page cache)中,也就是说,数据会先被拷贝到操作系统内核的缓冲区中,然后才会从操作系统内核的缓冲区拷贝到应用程序的地址空间。1.缓存I/O有以下优点:A.缓存I/O使用了操作系统内核缓冲区,
- 随想 生活
暗黑小菠萝
生活
其实账户之前就申请了,但是决定要自己更新一些东西看也是最近。从毕业到现在已经一年了。没有进步是假的,但是有多大的进步可能只有我自己知道。
毕业的时候班里12个女生,真正最后做到软件开发的只要两个包括我,PS:我不是说测试不好。当时因为考研完全放弃找工作,考研失败,我想这只是我的借口。那个时候才想到为什么大学的时候不能好好的学习技术,增强自己的实战能力,以至于后来找工作比较费劲。我
- 我认为POJO是一个错误的概念
windshome
javaPOJO编程J2EE设计
这篇内容其实没有经过太多的深思熟虑,只是个人一时的感觉。从个人风格上来讲,我倾向简单质朴的设计开发理念;从方法论上,我更加倾向自顶向下的设计;从做事情的目标上来看,我追求质量优先,更愿意使用较为保守和稳妥的理念和方法。
&
![]() 的拉氏变换存在的条件:
的拉氏变换存在的条件: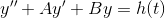
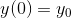 ,
,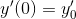
![\mathcal {L}[{y}''(t)]=s\cdot \mathcal {L}[{y}'(t)]-{y}'(0)=s[s\cdot \mathcal {L}[y(t)]-y(0)]-{y}'(0)](http://img.e-com-net.com/image/info8/ddd0cd21af0f4bcfa6b0dcb8ac5f8a51.gif)
![\mathcal {L}[{y}''(t)]=s^{2}\cdot \mathcal {L}[y(t)]-s\cdot y(0)-{y}'(0)](http://img.e-com-net.com/image/info8/690c6a90280c42298e39d4eee5a9e84a.gif)
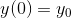 ,
,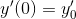
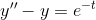
 ,
,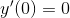
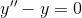
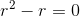
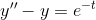
![\mathcal {L}[y]](http://img.e-com-net.com/image/info8/33ad7dc7e86f433093e7bff66e9a44b2.gif) :
:![\mathcal {L}^{-1}[\mathcal {L}[y]]=y(t)](http://img.e-com-net.com/image/info8/7c102b24a88f4284b1ded02434537b85.gif) :
: