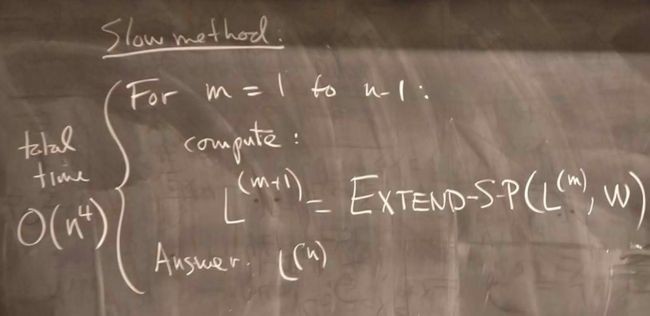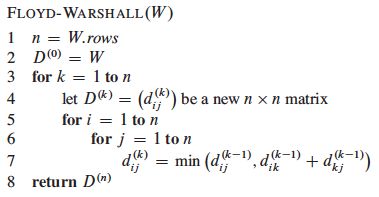最短路径问题算法（Shortest Path Problems' Algorithms）

最短路径问题算法

作者：Bluemapleman([email protected])

麻烦不吝star和fork本博文对应的github上的技术博客项目吧！谢谢你们的支持！

知识无价，写作辛苦，欢迎转载，但请注明出处，谢谢！

---

前言：最短路径问题可以根据要解决的具体问题类型，分为单源单目标最短路径(single pair)，单源最短路径(single source)，单目标最短路径(single destination),和多源多目标最短路径问题（all pairs）。我们从单源最短路径问题入手，单目标最短路径问题等价于反向的单源最短路径问题，单源单目标最短路径问题则是一个顺便解决的问题，而多源多目标最短路径问题的解决方案也是基于单源最短路径问题的。

本博文谈论最短路径问题中，除非特别说明，否则默认都是有向图（Digraph）:G=(V,E)，V表示顶点集合，E表示边集合。

单源最短路径问题

设定

• 有向图
• 单一起始点
• 每条边都是加权有向边（Weighted directed edges），连接顶点a和顶点b之间的边的权重用w(a,b)表示
• 每个顶点都有一个key，名为d，表示从源点s到达该顶点的最短距离.(s.d=0)；并且每个点有一个属性prev来记录最短路径上的前继顶点(s.prev=s)。

引入

• 最短路径与最短子路径

容易观察到的一个最短路径相关的性质是：若有一条从任意a点到b点的最短路径，则该路径上任意两点之间的路径也是这两点之间的最短路径。（容易通过反证法证明）

• 最短路径存在性质

显然，如果图中没有负值回路（negative cycles，即所有边的权值和为负数的回路），并且如果从点s到点t之间有至少一条路径可达，则一定存在一个从s到t的最短路径，并且该路径一定是简单（simple，即没有重复走过的顶点）的。

如果有负值回路，会造成的情况是：某最短路径可以通过不断走负值回路降低路径总长度，所以导致最短路径可以无限短，也就没有了真正意义上的最短路径。

• 松弛操作(RELAX)

松弛操作接受点a，点b，以及从点a指向b的边的权重w三个参数，并进行如下操作：

RELAX(a,b,w)
IF b.d>a.d+w:
    b.d=a.d+w;
    b.prev=a.prev;

该操作的含义就是，若目标点的key当前大于【某边的源点的key+边的权重的和】，则将该目标点的key设置为这个和，即表示点b可以通过将点a设为前缀顶点，并走边w(a,b)，以实现更短的到达路径。

Bellman-Ford算法

Bellman-Ford算法是解决单元最短路径的一个算法，其做法是：重复V-1次，对图的所有的E条边进行松弛操作。并且，Bellman-Ford算法中允许边的权重为负数，即w(a,b)<0

• 伪代码

BELLMAN-FORD(G,w,s)
1 INITIALIZE-SINGLE-SOURCE(G,s) // 初始化步骤：设置所有顶点的key
2 for i=1 to |G.V| - 1          // 重复V-1次：对所有的边进行松弛操作
3   for each edge (u,v) in G.E
4     RELAX (u,v,w)
5   for each edge(u,v) in G:E   // 5-7行检查是否有负值回路，有则不存在最短路径
6     if v.d > u.d + w(u,v)
7       return FALSE
8   return TRUE

时间复杂度：O(VE)

一种直观的改进思路是：在每轮循环中用一个标记变量记录本轮是否有有松弛操作生效，若没有，说明已经到达最终情况，可以退出松弛的循环。（类似布尔排序的改进。）

而如果存在负值回路，在算法跑完后，我们也可以通过前继结点的回溯发现一个环。

DAG的单源最短路径算法

DAG（Directed acyclic graph）即有向无环图，相比Bellman-Fold算法还必须注意负值回路的问题，DAG则通过限定无环避免了这个问题。而我们针对这类常见的图，就可以用拓扑排序的方法在O(V+E)的时间复杂度内解决图内的单源最短路径问题：

DAG-SHORTEST-PATHS(G,w,s)
1 topologically sort the vertices of G // 拓扑排序，O(V+E)
2 INITIALIZE-SINGLE-SOURCE(G,s)  // 初始化 O(V)
3 for each vertex u, taken in topologically sorted order // 3-5行对按照拓扑排序的顺序，对每个顶点的边逐一进行松弛操作，O(V)
4   for each vertex v in G.Adj(u)
5     RELAX(u,v,w)

Dijkstra算法（迪杰斯特拉算法）

在Bellman-Fold和DAG单元最短路径算法中，都允许权重为负数的边存在，而Dijkstra最短路径算法则不允许权重为负数的边存在。

DIJKSTRA(G,w,s)
1 INITIALIZE-SINGLE-SOURCE(G,s)
2 S = null set
3 Q = G.V   // 建立优先队列, O(VlgV)时间复杂度，O(V)空间复杂度
4 while Q != null set ;
5   u = EXTRACT-MIN(Q)  // 优先队列的提取key最小的顶点的操作
6   S = S union {u}
7   for each vertex v in G.Adj[u]
8     RELAX(u,v,w)      // DecreaseKey操作

Dijkstra算法用到了优先队列来实现，先将所有顶点通通入队，然后按照key从小到大的顺序出队并进行松弛操作，而先出队的顶点的松弛操作可能影响尚未出队的顶点的key值大小，因此我们用DecreaseKey操作保证尚未出队的顶点在队列中的正确相对顺序。

Dijkstra的时间复杂度主要取决于我们如何实现优先队列，甚至我们可以不用优先队列，而只用一个数组来存顶点的key值，并通过遍历数组来找key最小的顶点。以下几种实现方式分别的复杂度：

• 数组存key代替优先队列: O(V^2+E)
• 最小二叉堆实现的优先队列: O(VlgV+ElgV)
• Fibonacci堆实现的优先队列：O(VlgV+E) (Fibonacci的DecreaseKey操作的时间复杂度是O(1))

空间复杂度则都是O(V)。

(从利用了优先队列和复杂度来看，Dijkstra和MST的Prim算法很像。)

多源多目标最短路径问题

设定

• 有向图
• 每条边都是加权有向边（Weighted directed edges）
• 每个顶点都有一个key，名为d，表示从源点s到达该顶点的最短距离.(s.d=0)；并且每个点有一个属性prev来记录最短路径上的前继顶点(s.prev=s)。

稀疏图——Johnson算法

• 适合解决稀疏图（E<
• 允许存在负数权重边

Johnson算法的整体思路是：先运行Bellman-Fold算法一遍，然后分别以各个顶点为源点，运行Dijkstra算法N遍。

但是首先注意，我们说过，Dijkstra算法是不允许存在负数边的，因此我们需要做一个reweighting操作，以重新构建整个图的边的权重，但不能影响最终结果。

reweighting的做法是这样的：

假设我们有一个“高度”函数（height function）：

  h: V -> R

我们可以定义reweighting:

  w'(u,v)=w(u,v)+h(u)-h(v)

假设P是这样一条路径：v0->v1->v2->...->vk

则reweighting前的路径权重和为：w(P)=w(v0,v1)+w(v1,v2)+...+w(vk-1,vk)

而reweighting后的路径权重和为：w'(P)=w(P)+h(v0)-h(vk)

我们希望尽量找到这样的一个h函数，使得所有的reweighting过的边的权重都为非负数。

• Johnson算法的具体步骤

Step 1: 添加一个新结点s，并添加从s到所有图G中的顶点的边，这些边的权重都初始化为0.这个新图，我们称之为G’.

Step 2: 运行一次Bellman-Ford算法；如果发现了负值回路，则退出；否则，令高度函数h(v)=$\delta (s,t$，即从s到v的最短路径长，并定义w’(u,v)=w(u,v)+h(u)-h(v). (通过Bellman-Fold的算法可知，w(u,v)+h(u)>=h(v)，所以w’(u,v)>=0)

Step 3: 基于w’，对每个V中的顶点运行一次Dijkstra算法。

Step 4: 输出所有s到所有t的最短路径$\delta (s,t)=\hat{\delta }(s,t)-h(s)+h(t)$

时间复杂度：$O(VE+VE+V^{2}lgV)=O(VE+V^{2}lgV)$ (基于Fibonacci Heap的优先队列实现)

空间复杂度：$O(V^2+V+V)=O(V^2)$

稠密图——矩阵乘法/Floyd-Warshall算法

如果我们的图是个稠密图（dense），即$E=\Theta (V^2)$：

矩阵乘法（Matrix Multiplication）算法

若图的边的权重以矩阵的形式给出：

n*n矩阵:W=($w_{ij}$), n=|V|,

$w_{ij}=$

• 0, 若i=j
• w(i,j)，若(i,j)$\in$E
• 无穷大，otherwise

定义另一个矩阵$L^{(m)}=(l_{ij}^{(m)})$:

l_{ij}^{(m)}=用小于m个边实现的从顶点i到顶点j的最短路径的长度。

而我们的最终目标就是计算$L^{(n)}$，而我们初始状态下拥有的是$L^{(1)}=W，即权重矩阵。$

• 时间复杂度为$O(n^4)的方法(Slowmethod)：$

EXTEND-S-P操作具体如下，它的含义就是基于当前的矩阵$L^{(i-1)}$，为每个最短路径多延伸一条边，得到$L^{(i)}$。

• 更好的$O(n^{3}lgn)$方法

“重复平方”：利用平方更快地得到$L^{(n)}$

Floyd-Warshall算法

初始状态下，我们有权重矩阵W,V={1,2,3,…,n}（给所有顶点编号），权重矩阵的元素$w_{ij}$为从点i到点j的边的权重，同时也可以看作是从点i到点j的、要求一步以内就能到达的最短路径。

定义$d_{ij}^{(k)}=$从i到j的最短路径，要求路径上所有途径点的编号都不大于k。

定义$D^{(k)}=(d_{ij}^{(k)})$，而我们最终想要的就是$D^{(n)}$.

• 算法描述

时间复杂度：$\Theta (n^3)$ (每个$D^{(i-1)}到D^{(i)}$的运算花费$O(n^2)$)

空间复杂度：$\Theta (n^3)$（如果存储所有的$D^{(i)}$）,$\Theta (n^2)$(如果只存储当前需要用到的$D^{(i)}$)

比较多源多目标最短路径算法

算法	时间复杂度
矩阵相乘算法	$O(n^{3}lgn)$
Floyd-Warshall算法	O($n^3$)
Johnson算法	O(nm+$n^{2}lgn$)

另外，矩阵相乘算法和Floyd-Warshall算法也需要做负值回路检测，以确保存在解。检测的方法时：只要在算法进行过程中发现任何$l_{ij}^{(m)}$或者$d_{ij}^{(k)}$为负值，就说明有负值回路。

单源单目标最短路径算法

我们重新回头看单源单目标最短路径算法问题：我们当然可以用单源最短路径算法像Bellman-Fold,DAG最短路径或者Dijkstra来解决，但是当然也没必要这样”高射炮打蚊子“，其实有专门针对这种问题的算法A*搜索，这里就不细讲了。

参考文献

[1] Introduction to Algorithms: Third Edition, Thomas et al.