《深度学习入门:基于Python的理论与实现》学习与总结（一）

一、博主有话要说

        此书是无意间在图书馆找深度学习的书籍时查询到的。对于一个刚刚接触深度学习，想要往图像识别这方向入门学习的新手而言，这本书很适合。

        由简入深，深而有度。认真地慢慢地阅读可以发现，此书讲解的知识点有序，可让读者很好理解。更多优点，大家可以自行去探索。

       在此，博主只简单总结（回顾）一些自己还需好好理解的内容。

 

二、学习ing

（一）NumPy

1、介绍：其为外部库（即需要 import），提供和处理 N 维数组对象 array，用来存储和处理大型矩阵。

2、导入 numpy 库，并生成 numpy数组，及简单的运算，输出结果如下图：

import numpy as np   # 导入库

x = np.array([1.0, 2.0, 3.0])   # 生成一维数组，即向量x
y = np.array([2.0, 4.0, 5.0])   # 向量y

    

3、numpy 生成 N 维数组：

# 注意：“张量” 或 “多维数组”，为三维数组及三维以上的数组
A = np.array([[1, 2], [3, 4]])   # 生成二维数组（矩阵），即 2 * 2 的矩阵A
B = np.array([[3, 0], [0, 6]])   # 2 * 2 的矩阵B

4、 访问元素：

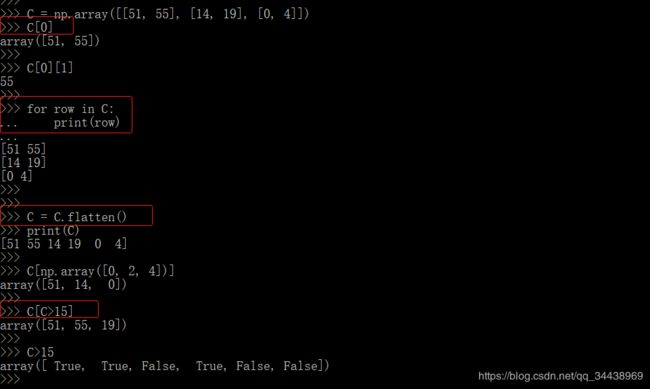
C = np.array([[51, 55], [14, 19], [0, 4]])   # 张量C

# 访问元素可用三种方法：
# 法一：
C[0]   # 元素的索引从0开始
C[0][1]

# 法二：
for row in C:
    print(row)

# 法三：
C = C.flatten()   # 将 C 转换为一维数组
C[np.array([0, 2, 4])]   # 获取索引为0，2，4的元素

'''
抽取 C > 15 的元素
'''
C[C>15]

 

(二）Matplotlib

1、介绍：用于绘制图形（如直方图，功率谱，条形图，错误图，散点图等）的 2D 库，实现数据的可视化。

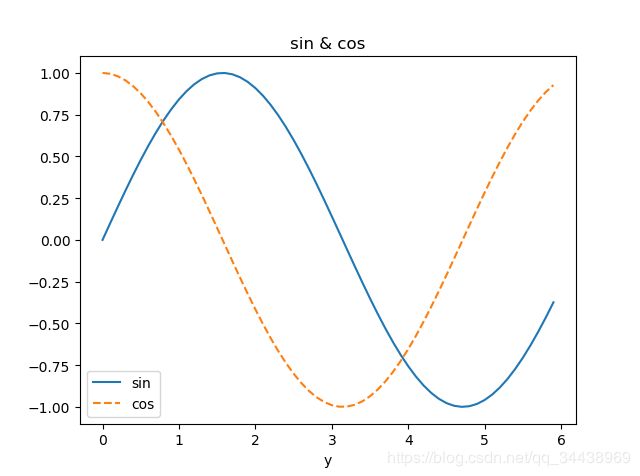
2、绘制简单图形：

import numpy as np
import matplotlib.pyplot as plt   # 导入 matplotlib 的 pyplot 模块

# 生成数据
x = np.arange(0, 6, 0.1)   # 以0.1为单位，生成0到6的数据
y1 = np.sin(x)
y2 = np.cos(x)

# 绘制图形
plt.plot(x, y1, label="sin")   # 默认用实线
plt.plot(x, y2, linestyle="--", label="cos")   # 用虚线绘制
plt.xlabel("x")   # x轴标签
plt.xlabel("y")   # y轴标签
plt.title('sin & cos')   # 标题
plt.legend()
plt.show()   # 显示图形

# plt.plot(x, y1) # 画出 y1 函数

3、（重点）显示图像

import matplotlib.pyplot as plt   # 导入 matplotlib 的 pyplot 模块
from matplotlib.image import imread   # 使用 matplotlib.image 的 imread() 方法读入图像

img = imread('mydog.JPG')   # 读入图像（此图像与当前文件的目录下）
plt.imshow(img)
plt.show()   # 显示图形

 

（三）感知器（perceptron）

1、介绍：神经网络的组成单元——神经元。神经元也叫做感知器，其是具有输入和输出的算法。给定一个输入后，将输出一个既定的值。

① 单层感知器（如与门、或门）只能表示线性空间，多层感知器（在理论上可表示计算机）可表示非线性空间；

② 使用 2 层感知机才可表示异或门。

③ 欲继续深入了解，可查看 https://www.zybuluo.com/hanbingtao/note/433855

2、实现与门（AND）、非门（NAND）、或门（OR）、异或门（XOR）函数

import numpy as np

# 与门
def AND(x1, x2):
    x = np.array([x1, x2])   # 输入
    w = np.array([0.5, 0.5])   # 权重，控制输入信号的重要性参数
    b = -0.7   # 偏置，调整神经元被激活的容易程度（输出信号为1的程度）的参数
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

# 非门
def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])   # 仅权重和偏置和 AND 不同
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

# 或门
def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])  # 仅权重和偏置和 AND 不同
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

# 异或门
def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y