经典遗传算法(SGA)解非线性最优化问题的原理及其python(python3.6)代码实现
1.多峰非线性最优化问题
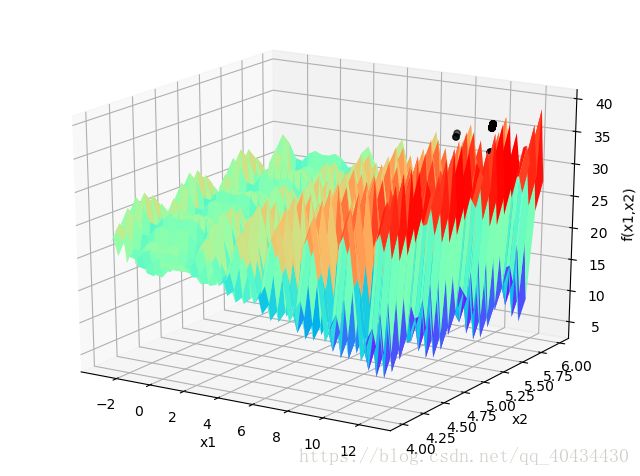
非线性最优化问题一直是学者研究的热点问题之一。下面考虑两个变量的非线性最优化问题,这个问题具有多个局部解,是多峰问题。下图是采用经典遗传算法找到的最优解在目标函数的三维图形中的分布情况,由于多峰最优化问题具有多个局部解的特性,使用传统的方法非常难获得最优解。
s . t . m a x f ( x 1 , x 2 ) = 21.5 + x 1 s i n ( 4 ∗ p i ∗ x 1 ) + x 2 s i n ( 20 ∗ p i ∗ x 2 ) − 3.0 ⩽ x 1 ⩽ 12.1 4.1 ⩽ x 2 ⩽ 5.8 s.t. \begin{matrix} max f(x_1,x_2)=21.5+x_1sin(4*pi*x_1)+x_2sin(20*pi*x_2) \\-3.0\leqslant x_1\leqslant 12.1 \\4.1\leqslant x_2\leqslant 5.8 \end{matrix} s.t.maxf(x1,x2)=21.5+x1sin(4∗pi∗x1)+x2sin(20∗pi∗x2)−3.0⩽x1⩽12.14.1⩽x2⩽5.8
目标函数的python代码如下:
#目标函数
def aimfun(x):
y=21.5+x[0]*math.sin(4*math.pi*x[0])+x[1]*math.sin(20*math.pi*x[1])
return y
下面我们根据此问题介绍经典的遗传算法。
2. 经典遗传算法
2.1 遗传算法概述
遗传算法是一种基于生物遗传机理,即生物进化(自然淘汰,交叉,变异等)现象的随机搜索算法,它通过计算机模拟生物进化过程来进行搜索和进化,最后寻求最优解,是一种超启发式算法,其中被称为个体的染色体(即研究对象的候选解)的集合能适应外部环境(研究对象的评价函数),并基于下面的规则在每代中生成新个体集合:
(1)越是适应性强的个体,其生存几率越高(自然选择);
(2)以原有个体为基础通过遗传操作生成新个体(遗传现象)。
其中(1)可看做是概率搜索法,(2)是经验搜索法。
2.2 染色体设计(编码和解码)
这里采用二进制字符编码法(binary-string encoding)来表示非线性优化的编码,以下是算法的伪代码,random[0,1]表示在[0,1]区间内随机产生0或者1。
procedure:binary-string encoding
input:no.of required bits m
output:chromosome vk
begin
for i=1 to m
vk(i)<--random[0,1];
output:chromosome vk;
end
编码(种群初始化)的python代码如下:
#初始化种群
def init(pop_num,chromo_len):
population=[]
for i in range(pop_num):
pop=''
for k in chromo_len:
for j in range(k):
pop=pop+str(np.random.randint(0,2))
population.append(pop)
return population
这里以二进制字符串来表示决策变量 x 1 , x 2 x_1,x_2 x1,x2。例如 x j x_j xj的定义域为 [ a j , b j ] [a_j,b_j] [aj,bj],而要求精度的小数点后5位,这就要求 x j x_j xj的定义域至少要划分为 ( b j − a j ) ∗ 1 0 5 (b_j-a_j)*10^5 (bj−aj)∗105个空间。设变量 x j x_j xj所需要的二进制字符串长为 m j m_j mj,则应满足:
2 m j − 1 < ( b j − a j ) ∗ 1 0 5 < 2 m j − 1 2^{m_j-1}<(b_j-a_j)*10^5<2^{m_j}-1 2mj−1<(bj−aj)∗105<2mj−1
例如精度都设置为小数点后5位,则两个变量所需的串长分别为18和15,总串长为33,则设置初始染色体的长度为33位。
获得染色体长度的python代码如下:
#获得染色体长度
def getchromolen(delta, upper,lower):
maxlen=25
chromo_len=[]
for j in range(len(upper)):
a=(upper[j]-lower[j])/delta[j]
for i in range(maxlen):
if (2**i < a) and (a < (2**(i+1))):
chromo_len.append(i+1)
break
return chromo_len
要想将变量 m j m_j mj由二进制转为十进制,可根据定义域范围内 2 m j − 1 2^{m_j}-1 2mj−1个划分点的位置,按下式计算:
x j = a j + d e c i m a l ( s u b s t r i n g j ) ∗ ( b j − a j ) / ( 2 m j − 1 ) x_j=a_j+decimal(substring_j)*(b_j-a_j)/(2^{m_j}-1) xj=aj+decimal(substringj)∗(bj−aj)/(2mj−1)
这里 d e c i m a l ( s u b s t r i n g j ) decimal(substring_j) decimal(substringj)表示变量 x j x_j xj的子串 s u b s t r i n g j substring_j substringj的十进制值。
解码的伪代码如下:
procedure:binary-string decoding
input:no.of bariables n,
no.of bits mj(j=1,2,...,n)
range[aj,bj] of variable xj(j=1,2,...,n)
chromosome vk
output:real number xj(j=1,2,...,n)
begin
s<--0,t<--0;
for j=1 to n
s<--t+1;
t<--t+mj;
xj=aj+((bj-aj)/(2^mj-1))*sum_{i=s->t}(2^(mj-i)*vk(i));
end
output:real number xj(j=1,2,...,n);
end
解码的python代码如下:
#解码
def decode(x,chromo_len,upper,lower):
y=[]
index=0
for i in range(len(chromo_len)):
a = lower[i]+(int(x[index:(index+chromo_len[i])],2))*(upper[i]-lower[i])/(2**chromo_len[i]-1)
y.append(a)
index = index+chromo_len[i]
return y
2.3 遗传操作
2.3.1轮盘赌模型
轮盘赌模型的基本原理是根据每个染色体的适值比例来确定该个体的选择概率或生存概率。如下面的伪代码那样,个体适应度按比例转换为轮盘的面积并旋转轮盘,最后选择球落点位置所对应的个体。(此处输入可以为父代加子代,也可直接输入子代,具体区别见后面的2.4算法流程)
这里有一些参数说明:
l:染色体索引号
F:所有染色体的适值和
vk:第k个染色体
pk:第k个染色体的选择概率
qk:前k个染色体的累计概率
procedure:roulette wheel selection
input:chromosome Pk,k=1,2,...,popsize+offsize
output:chromosome Pk in next generation
begin
计算适应度函数值eval(Pk);
计算累计适应度F=sum_{k=1->popsize+offsize}eval(Pk);
计算选择概率pk=eval(Pk)/F(k=1,2,...,popsize+offsize);
计算累计概率qk=sum_{i=1->k}pi(k=1,2,...,popsize+offsize);
for k=1 to popsize
r<--random[0,1]
if r<=q1 then
Pl'<--Pk;
else if qk-1适应度值计算和轮盘赌的python代码如下;
#适应度函数
def fitnessfun(population,aimfun,chromo_len,upper,lower,fun):
value=[]
for i in range(len(population)):
valuea=aimfun(decode(population[i],chromo_len,upper,lower))
value.append(valuea)
if fun==0:
minvalue=min(value)
value=[(i-minvalue+0.0000001) for i in value]
elif fun==1:
maxvalue=max(value)
value=[(maxvalue-i+0.0000001) for i in value]
return value
#轮盘赌选择
def roulettewheel(population,value,pop_num):
fitness_sum=[]
value_sum=sum(value)
fitness=[i/value_sum for i in value]
for i in range(len(population)):##
if i==0:
fitness_sum.append(fitness[i])
else:
fitness_sum.append(fitness_sum[i-1]+fitness[i])
population_new=[]
for j in range(pop_num):###
r=np.random.uniform(0,1)
for i in range(len(fitness_sum)):###
if i==0:
if r>=0 and r<=fitness_sum[i]:
population_new.append(population[i])
else:
if r>=fitness_sum[i-1] and r<=fitness_sum[i]:
population_new.append(population[i])
return population_new
2.3.2单点交叉
随机选择父母双方染色体上的一个点,并指定为“交叉点”。在该点右侧的位在两个亲本染色体之间进行交换。这样导致每个后代都携带了来自父母的一些遗传信息。此算法父代的双亲个体有可能被多次选择,也可能一次都未选到,即不满足完备性(父代中的个体不是所有都被选择)。此算法也可以让父代的双亲个体都被选择,即满足完备性。以下的算法伪代码为前者,实现的python代码为后者。
参数说明:
pc:交叉概率
p:交叉点
L:为染色体长度
input: pc, parent Pk, k=1, 2, ..., popsize
output: offspring Ck
begin
for k <-- 1 to popsize/2 do
if pc≥random[0,1] then
i<--0;
j<--0;
repeat
i<--random[1,popsize];
j<--random[1,popsize];
until(i≠j)
p<--random[1,L-1];
Ck<--Pi[1:p-1]//Pj[p:L];
C(k+popsize/2)<--Pj[1:p-1]//Pi[p:L];
end
end
output:offspring Ck;
end
单点交叉的python代码如下:
#单点交叉
def crossover(population_new,pc,ncross):
a=int(len(population_new)/2)
parents_one=population_new[:a]
parents_two=population_new[a:]
np.random.shuffle(parents_one)
np.random.shuffle(parents_two)
offspring=[]
for i in range(a):
r=np.random.uniform(0,1)
if r<=pc:
point=np.random.randint(0,int(len(parents_one[i])/2))
off_one=parents_one[i][:point]+parents_two[i][point:]
off_two=parents_two[i][:point]+parents_one[i][point:]
ncross = ncross+1
else:
off_one=parents_one[i]
off_two=parents_two[i]
offspring.append(off_one)
offspring.append(off_two)
return offspring
2.3.3反转变异(单点变异)
实现单点变异算子的常用方法1为每条染色体随机生成一个数,此数指示该染色体是否需要变异。如果该染色体需要变异,为其生成一个随机变量,此随机变量指示修改该染色体的哪一位。其算法的伪代码如下:
procedure:mutation1
input: pm, parent Pk, k=1, 2, ..., popsize // pm:变异概率
output: offspring Ck
begin
for k <-- 1 to popsize do
if pm <-- random [0, 1] then
point<--random[0,L-1] // L: 染色体长度
if point = 0
Pk <-- 1-Pk [ 0 ] // Pk[ 1: L ];
else
Pk <-- Pk [1: point-1] // 1-Pk [ point ] // Pk[ point+1: L ];
end
end
Ck =Pk;
end
output:offspring Ck;
end
反转变异1的python代码如下:
#单点变异1
def mutation1(offspring,pm,nmut):
for i in range(len(offspring)):
r=np.random.uniform(0,1)
if r<=pm:
point=np.random.randint(0,len(offspring[i]))
if point==0:
if offspring[i][point]=='1':
offspring[i]='0'+offspring[i][1:]
else:
offspring[i]='1'+offspring[i][1:]
else:
if offspring[i][point]=='1':
offspring[i]=offspring[i][:(point-1)]+'0'+offspring[i][point:]
else:
offspring[i]=offspring[i][:(point-1)]+'1'+offspring[i][point:]
nmut = nmut+1
return offspring
实现单点变异算子的常用方法2为染色体数组中的每个位生成随机变量。此随机变量指示是否将修改特定位。其算法的伪代码如下:
procedure:mutation2
input: pm, parent Pk, k=1, 2, ..., popsize // pm:变异概率
output: offspring Ck
begin
for k <-- 1 to popsize do
for j <-- 1 to L do(基因串长度) // L: 染色体长度
if pm <-- random [0, 1] then
Pk <-- Pk [1: j-1] // 1-Pk [ j ] // Pk[ j+1: L ];
end
end
Ck =Pk;
end
output:offspring Ck;
end
反转变异2的python代码如下:
#单点变异2
def mutation2(offspring,pm,nmut):
for i in range(len(offspring)):
for j in range(len(offspring[i])):
r=np.random.uniform(0,1)
if r<=pm:
if j==0:
if offspring[i][j]=='1':
offspring[i]='0'+offspring[i][1:]
else:
offspring[i]='1'+offspring[i][1:]
else:
if offspring[i][j]=='1':
offspring[i]=offspring[i][:(j-1)]+'0'+offspring[i][j:]
else:
offspring[i]=offspring[i][:(j-1)]+'1'+offspring[i][j:]
nmut = nmut+1
return offspring
2.4 算法流程
应用经典遗传算法对多峰非线性问题求解的总体流程伪代码如下:(此处由于对轮盘赌操作的输入种群不同,因此列出两种代码,请读者加以区别。)
GA的算法流程为伪代码如下:
procedure:simple GA
input: GA parameters
output: the best solution
begin
t<-- 0 // t:遗传代数
initialize P(t) by encoding routine; //P(t):染色体种群
fitness eval(P) by decoding routine;
while (not termination condition) do
crossover P(t) to yield C(t); //C(t):offspring
mutation P(t) to yield C(t);
fitness eval(C) by decoding routine;
select P(t+1) from P(t) and C(t);
t<--t+1;
end
output:the best solution;
end
GA的python代码1如下(轮盘赌的输入为父代加子代):
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import math
#参数设置-----------------------------------------------------------------------
gen=1000#迭代次数
upper=[12.1,5.8]#自变量上界
lower=[-3.0,4.1]#自变量下界
pc=0.25#交叉概率
pm=0.01#变异概率
pop_num=10#种群大小
delta=[0.0001,0.0001]#编码精度
fun=0#0最大化,1最小化
#初始化-------------------------------------------------------------------------
#获得编码长度
chromo_len = getchromolen(delta,upper,lower)
#初始化种群
population=init(pop_num,chromo_len)
#初始化交叉个数
ncross=0
#初始化变异个数
nmut=0
#储存每代种群的最优值及其对应的个体
t=[]
best_ind=[]
last=[]#储存最后一代个体的函数值
realvalue=[]#储存最后一代解码后的值
#循环---------------------------------------------------------------------------
for i in range(gen):
print("迭代次数:")
print(i)
#交叉
offspring_c=crossover(population,pc,ncross)
#变异
#offspring_m=mutation1(offspring,pm,nmut)
offspring_m=mutation2(offspring_c,pm,nmut)
mixpopulation=population+offspring_m
#适应度函数计算
value = fitnessfun(mixpopulation,aimfun,chromo_len,upper,lower,fun)
#轮盘赌选择
population=roulettewheel(mixpopulation,value,pop_num)
#储存当代的最优解
result=[]
if i==gen-1:
for j in range(len(population)):
bb = decode(population[j],chromo_len,upper,lower)
result.append(aimfun(bb))
realvalue.append(bb)
last=result
else:
for j in range(len(population)):
result.append(aimfun(decode(population[j],chromo_len,upper,lower)))
maxre=max(result)
h=result.index(max(result))
#将每代的最优解加入结果种群
t.append(maxre)
best_ind.append(population[h])
GA的python代码2如下(轮盘赌的输入为子代):
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import math
#参数设置-----------------------------------------------------------------------
gen=1000#迭代次数
upper=[12.1,5.8]#自变量上界
lower=[-3.0,4.1]#自变量下界
pc=0.25#交叉概率
pm=0.01#变异概率
pop_num=10#种群大小
delta=[0.0001,0.0001]#编码精度
fun=0#0最大化,1最小化
#初始化-------------------------------------------------------------------------
#获得编码长度
chromo_len = getchromolen(delta,upper,lower)
#初始化种群
population=init(pop_num,chromo_len)
#初始化交叉个数
ncross=0
#初始化变异个数
nmut=0
#储存每代种群的最优值及其对应的个体
t=[]
best_ind=[]
last=[]#储存最后一代个体的函数值
realvalue=[]#储存最后一代解码后的值
#循环---------------------------------------------------------------------------
for i in range(gen):
print("迭代次数:")
print(i)
#适应度函数计算
value = fitnessfun(population,aimfun,chromo_len,upper,lower,fun)
#轮盘赌选择
population=roulettewheel(population,value,pop_num)
#交叉
offspring_c=crossover(population,pc,ncross)
#变异
#offspring_m=mutation1(offspring,pm,nmut)
offspring_m=mutation2(offspring_c,pm,nmut)
population=offspring_m
#储存当代的最优解
result=[]
if i==gen-1:
for j in range(len(population)):
bb = decode(population[j],chromo_len,upper,lower)
result.append(aimfun(bb))
realvalue.append(bb)
last=result
else:
for j in range(len(population)):
result.append(aimfun(decode(population[j],chromo_len,upper,lower)))
maxre=max(result)
h=result.index(max(result))
#将每代的最优解加入结果种群
t.append(maxre)
best_ind.append(population[h])
3. 实验结果
本实验参数设置如下:
1.gen=1000#迭代次数
2.upper=[12.1,5.8]#自变量上界
3.lower=[-3.0,4.1]#自变量下界
4.pc=0.25#交叉概率
5.pm=0.01#变异概率
6.pop_num=10#种群大小
7.delta=[0.0001,0.0001]#编码精度
根据上述参数设置和原理分析,我们编程得到最后一代解的分布如下图所示。
其每代最优的函数值随进化代数的变化如下图所示。
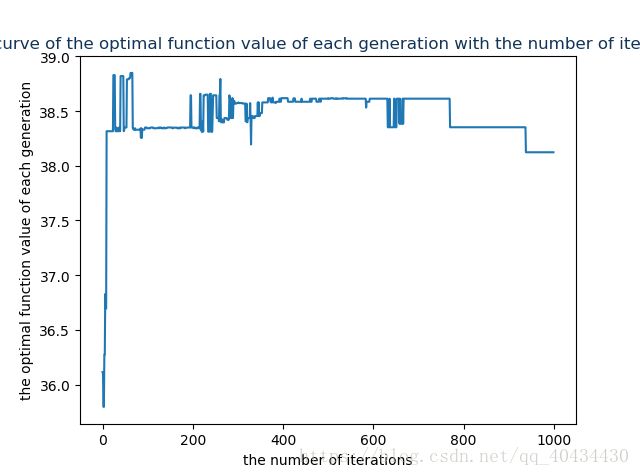
很明显算法最后可以收敛到一个较好的解,如果想要得到最优的解,还需要做大量的实验从而选择较合适的参数,建议读者可以多多进行尝试。
画图的python代码如下:(接到主程序后就行)
#输出结果-----------------------------------------------------------------------
best_value=max(t)
hh=t.index(max(t))
print(best_value)
print(decode(best_ind[hh],chromo_len,upper,lower))
#画出收敛曲线
plt.plot(t)
plt.title('The curve of the optimal function value of each generation with the number of iterations',color='#123456')
plt.xlabel('the number of iterations')
plt.ylabel('the optimal function value of each generation')
#画出函数与解的分布
fig = plt.figure()
ax = Axes3D(fig)
x1 = np.arange(-3,13,0.4)
x2 = np.arange(4,6,0.0460)
X, Y = np.meshgrid(x1,x2)#网格的创建,这个是关键
Z=21.5+X*np.sin(4*np.pi*X)+Y*np.sin(20*np.pi*Y)
plt.xlabel('x1')
plt.ylabel('x2')
ax.set_zlabel('f(x1,x2)')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
ax.scatter(np.array(realvalue)[:,0], np.array(realvalue)[:,1], np.array(last),marker='o', c='k')
plt.show()
完整的python代码如下:https://download.csdn.net/download/qq_40434430/10742475
由于作者水平有限,以上内容难免有错误之处,如果读者有所发现,请在下面留言告知我,鄙人将不胜感激!
[1]:(日)玄光男, 林林等著. 网络模型与多目标遗传算法[M]. 于歆杰, 梁承姬译. 北京: 清华大学出版社, 2017