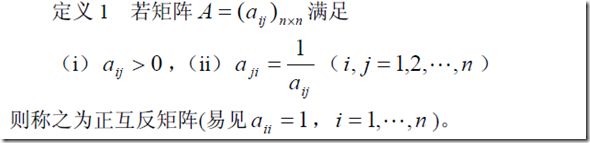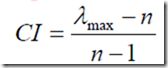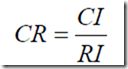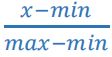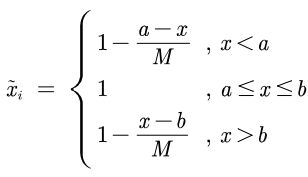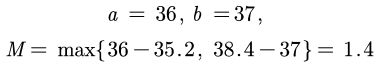数学建模day1 层次分析法与TOPSIS方法

原文链接：https://blog.csdn.net/qq_36384657/article/details/98188769

概念：

层次分析法（Analytic Hierarchy Process ，简称 AHP ）是对一些较为复杂、较为模糊的问题作出决策的简易方法，它特别适用于那些难于完全定量分析的问题。它是美国运筹学家T. L. Saaty 教授于上世纪 70 年代初期提出的一种简便、灵活而又实用的多准则决策方法

一、步骤

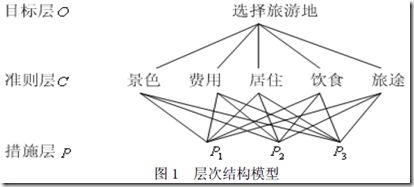
1、建立递阶层次结构模型

2、构造出各层次中的所有判断矩阵

3、层次单排序及一致性检验

4、层次总排序及一致性检验

二、递阶层次的建立与特点

1、分层：

（1）最高层：这一层次中只有一个元素，一般它是分析问题的预定目标和理想结果。

（2）中间层：这一层次中包含为了实现目标所涉及的中间环节，主要是一些考虑指标和一些准则。

（3）最底层：这一层次中包含为了实现目标可供选择的各种方案。

2、注意点：

一般不要1层不要超过9个因素

3、一个demo

是三个旅游景点

二、构造判断矩阵

由于准则层中的各准侧的权值可能不同，所以应该设置一个权重。

1、比较判别矩阵的元素意义

设现在要比较n个因子对某因素Z的影响大小，采用两两比较建立比较判别矩阵，xi与xj对Z的影响之比为aij。然后反过来xj与xi的影响之比为aji=1/aij。

2、比较判别矩阵的定义

3、关于比较判别矩阵元素的确定

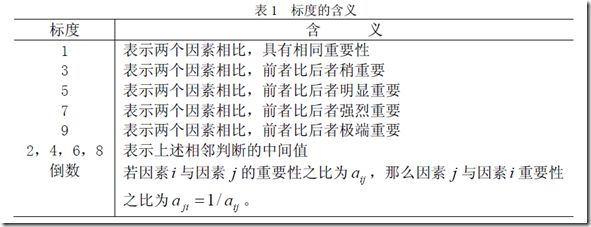
使用数字1-9以及其倒数作为标度。

三、层次单排序及一致性检验

1、原理

判断矩阵A对应于最大特征值得特征向量W，经归一化即为同一层次相应元素对于上一层次元素相对重要性的排序权值。称为层次单排序

因此，我们通过来检验A是否为一致矩阵，当比n大的越多，A的非一致性程度也就越严重，所以我们可以通过这种方法来检验一致性。

2、步骤

（1）计算一致性指标CI

（2）查询平均随机一致性指标RI，对应n=1到9，RI值分别为

这是通过随机的方法生成的一组标准指标。

（3）计算一致性比例CR

当CR<0.1，认为矩阵的一致性是可以接受的。

四、层次总排序及一致性检验

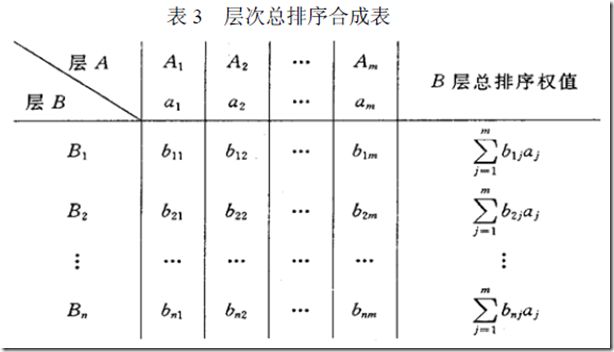
1、说明

（1）A为上一层次（高的层次），B为当前层次

（2）a1,a2,a3……am为A层次的总排序权重。

（3）b1j……bnj是B层对Aj的单排序权重。

（4）从最高层到最底层

现求B层中各因素关于总目标的权重，即求B层各因素的层次总排序权重b1,b2……bn。就按照上图中的方法进行计算。

2、然后对于层次总排序也要进行一致性检验。

当CR<0.10，认为层次总排序结果具有较满意的一致性并接受该分析结果。

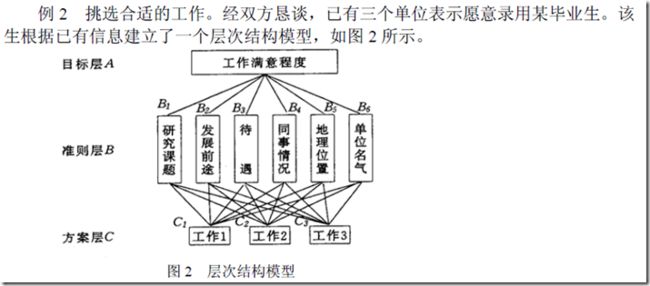
（二）层次分析法的应用

1、准则层的排序矩阵

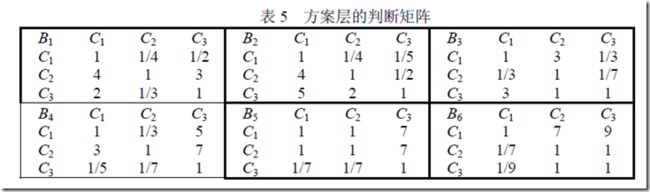
2、方案层的排序矩阵

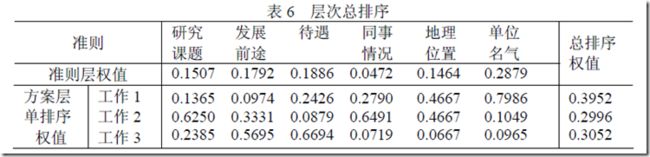
3、层次排序总结果

所以最满意的工作是1。

一、TOPSIS方法

TOPSIS法（Technique for Order Preference by Similarity to Ideal Solution） 可翻译为逼近理想解排序法，国内常简称为优劣解距离法 TOPSIS 法是一种常用的综合评价方法，其能充分利用原始数据的信息， 其结果能精确地反映各评价方案之间的差距。

基本过程为先将原始数据矩阵统一指标类型（一般正向化处理） 得到正向化的矩阵，再对正向化的矩阵进行标准化处理以消除各指标量纲的影响，并找到有限方案中的最优方案和最劣方案，然后分别计算各评价对象与最优方案和最劣方案间的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制，数据计算简单易行。

本部分的代码讲解部分参照第二篇博客：评价类模型——TOPSIS法（优劣解距离法）matlab代码实现 学习笔记（二）

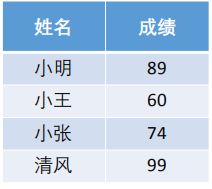
例题1：请你为以下四名同学进行评分，该评分能合理的描述其高数成绩的高低。

分析：此评价指标只有一项即“成绩”，评价对象为4个。topsis分析方法如下：

解：

1.取指标成绩中，最高成绩max ： 99 最低成绩min：60

构造计算评分的公式：

2.根据评分公式为每一评价对象进行打分，构建如下评分表格、并归一化

3.打分完成，接下来可以由评分确定谁的成绩最好，谁的最差。可见，清风的成绩最好，小王的最差

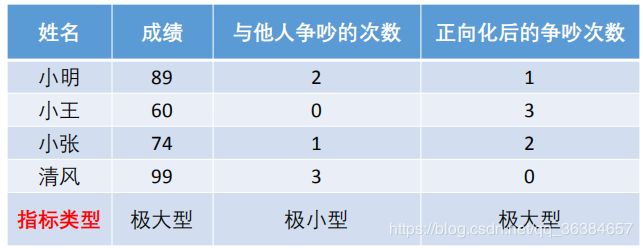
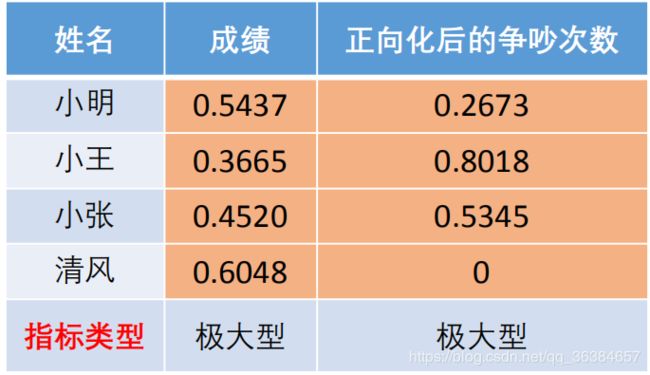
例题2：请你为以下四名同学进行评分，该评分能合理的描述其综合评价。

分析：例题1考虑的评价指标只有一个，例题2转化为两个评价指标，且评价时指标一（成绩）应该越大越好，指标二（与他人争吵次数）应该越小越好。这就引发矛盾，怎么确定评分使得兼顾两种不同取向的指标？

注：成绩是越高（大）越好，这样的指标称为极大型指标（效益型指标）。

与他人争吵的次数越少（越小）越好，这样的指标称为极小型指标（成本型指标）。

解：

1.将所有的指标转化为极大型指标，即指标正向化。

极小型指标转换为极大型指标的公式：max-x

正向化后得到的表格如下：

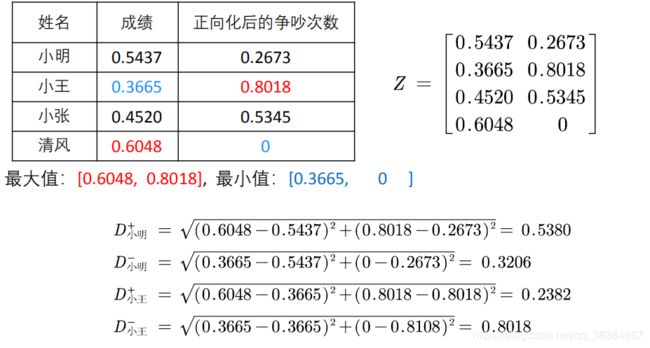
2. 为了消去不同指标量纲的影响， 需要对已经正向化的矩阵进行标准化处理。

标准化处理的计算公式

即每个元素除以其所在列各元素平方和的开方

3. 计算评分

首先看一下，两个指标的评分公式怎么推导的

类比只有一个指标计算得分

即：取各列元素的最大值，组成一个列向量Z+，取各列元素的最小值，组成一个列向量Z-，计算每列元素与最大值组成的列向量Z+的距离D+，与最小值组成的列向量Z-的距离D-，在根据评分公式：D-/(D+ + D-）为每个对象进行打分。

根据上面的评分公式，为各评价对象进行打分

4.打分完成，进行数据分析

由综合评分可以看出，小王的评分最高，其成绩和与他人争吵次数的综合评价指标中是最好的；清风最差，即使其成绩是最好的，但是在与他人争吵的评分这项指标中，其与他人差别过大，此项导致其综合评分最低，由此可见指标二的评分在整个评分中作用更关键。

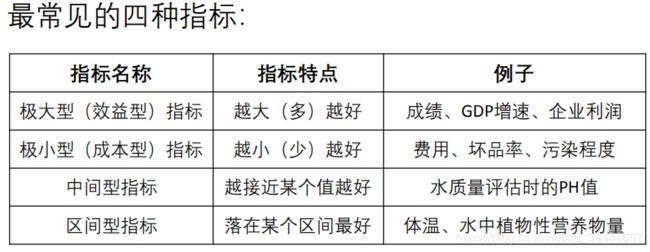
二、 其他指标正向化方法

前面介绍了评价指标只有一种、以及评价指标有两种，且一种是极小型指标的例子。在例题二中，极小型指标要转化为极大型指标才能参与运算，常见的还有其他两种非极大型指标：中间型和区间型指标。下面介绍其如何转为极大型，即指标正向化。

1）、中间型指标 ——>极大型指标

例如： 水质量评估 PH 值指标正向化，PH值取7时水质最好

2）、区间型指标——>极大型指标

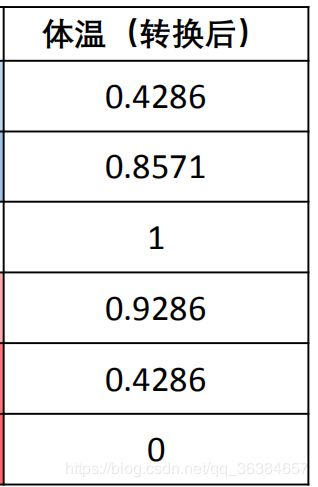
例如： 例如人的体温在36摄氏度~37摄氏度这个区间内最好

可以看出，在区间内的36.6度评分最高为1，距离其越远的评分越低

三、TOPSIS方法总结

1、如果有多个指标且不全是极大型指标，则进行指标正向化。

2、之后对正向化矩阵进行标准化，目的是消除不同指标量纲的影响。

正向化方法：

3. 计算得分

4.归一化评分

即每个分数除以所有分数和

综合例题4：评价下表中A-T共20条河流的水质情况

已知：含氧量越高越好；PH值越接近7越好；细菌总数越少越好；植物性营养物量介于10-20之间最佳，超

过20或低于10均不好。

解：1、将各项指标正向化

PH值（中间型转极大型）、细菌总数（极小型转极大型）、植物性营养物量（区间型转极大型）

2、正向化后的矩阵进行标准化

3、进行打分（20个评价对象，4个评价指标）

4、分数归一化

5、分析评分，最高得分的河流水质最好