半导体物理 第七章 金属半导体接触整流理论

二、金属半导体接触整流理论

A、前言概述（定性分析）

不知道大家还记不记上一个博客中的一个式子：

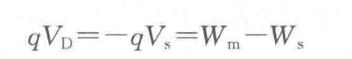
Vs是表面势，在我们经常讨论的那一个情况当中，Vs < 0；半导体一侧的势垒高度即为qVD = - qVs。若此时，我们外加电压V于紧密接触的金属和半导体之间，由于阻挡层是高阻区域，因此电压主要降落在阻挡层上，原本半导体的表面和内部之间的电势差，即表面势为Vs，现在应为Vs + V；

此时，我们又可以经典的分情况讨论问题啦！

一、V > 0
因为当下的Vs是小于0的，若V > 0， 则会导致Vs + V降低，便会导致半导体一侧势垒高度降低，这时，从半导体流到金属的电子便会增加，多于从金属流到半导体的电子，便会形成从金属流向半导体的正向电流。外加电压越大，势垒下降越多，正向电流也就越大。
二、V < 0
相反，若V < 0，则会导致Vs + V升高，便会导致半导体一侧势垒高度升高，从半导体流到金属的电子会减少，少于从金属流到半导体的电子，会形成从半导体流向金属的反向电流，随着电压的增大，势垒高度越来越高，从半导体流向金属的电子可以忽略不计，又因为金属的势垒高度基本不会受V的影响，所以反向电流渐渐趋于饱和值，且金属一侧的势垒高度是很高的，所以反向电流又是一个很小的值。

因此，我们可以看出金属半导体接触的整流特性，当然以上都仅仅只是基于理论来进行定性的分析，接下来我们便从定量的角度分情况去讨论一下金属半导体接触的整流特性曲线。

B、扩散理论（定量分析）

上面讲到了我们将进行分情况讨论，为什么需要分情况讨论呢？因为不同的情况所需要用到的理论是不一样的，我们这里用到的是势垒宽度Xd和电子的平均自由程的大小相比进行分情况讨论，而我们这里所要用到的扩散理论，是适用于势垒宽度Xd远大于电子的平均自由程的情况的。

在开始我们的理论定量分析之前，我们有必要去了解电子的平均自由程这个概念：

电子的平均自由程
电子的平均自由程指的是电子两次碰撞之间的时间内经过的路程的统计平均值，理想电子两次碰撞之间做匀速直线运动，电子的平均自由程与其自身的电子的直径，电子数密度成反比。

由于势垒宽度Xd远大于电子的平均自由程，所以电子通过势垒区需要发生多次的碰撞，这样的阻挡层被称为厚阻挡层

之后我们经过了一系列比较复杂的运算之后（还是需要后面自己去推算），这里直接给出我们几个重要的结果

势垒宽度Xd

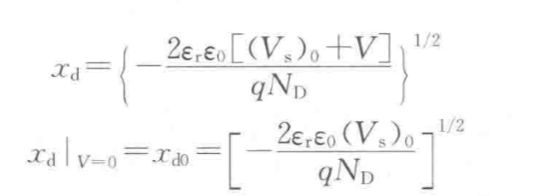
我们可以看出，我们若外加正向电压，V > 0 ，如此Vs + V便会降低，从而导致势垒宽度Xd降低；随着外加电压的增大，势垒宽度会越来越小；反之，则势垒宽度会越来越大。

扩散理论下的金属半导体接触电流

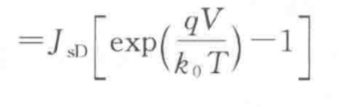
上图是电流密度的表达式

上图是电流密度当中的JsD的表达式

我们为了讨论更加的方便，不妨都假设在qV >> k0T 的情况之下：

V > 0
exp(qV / k0T)趋向于正无穷，可以忽略方程中的‘1’，电流密度方程是一个指数函数；
V < 0
qV / k0T趋向于负无穷，exp(qV / k0T)趋向于0，方程中剩下‘-1’，电流密度方程仅剩下-JsD；

综上，我们定型地得到扩散理论是满足我们的理论分析的。

C、热电子发射理论（定量分析）

对于我们的热电子发射理论的情况则和扩散理论的情况是相反的了，适用于电子平均自由程远大于势垒宽度的情况，在这种情况下，电子在势垒区的碰撞可以忽略，在这个时候，势垒的形状并不重要，起到决定作用的是势垒高度。半导体内部的电子只要有足够的能量越过势垒的顶点，就可以自由通过阻挡层进入金属；同样，金属中能超越势垒顶的电子也都能到达半导体内，所以呢，电流的计算就归结于计算超越势垒的载流子数目。

同样，在此处我们省略掉运算的过程直接给出最终的结果：

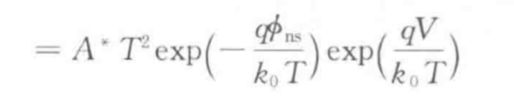
以上是由半导体到金属的电流密度

以上是有效理查逊常数A

而由金属到半导体的电流密度则是由外加电压为0的时候，与半导体到金属的电流密度在数值上相等，符号相反，原因是金属一侧的势垒高度不会随着外加电压的大小而发生变化，因此从金属流向半导体的电流密度是维持于一定的值的。

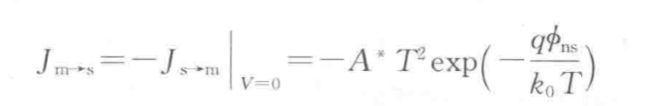
以上是由金属流到半导体的电流密度

因此，综上，我们便可以得到我们最终的电流密度：

以上是总的电流密度表达式

综上，两种情况的电流密度表达式基本上是一致的，只是在扩散理论下的JsD更加依赖于电压，而热电子发射理论下的JsT不依赖于外加电压，反而十分依赖于温度。

D、镜像力和隧道效应的影响

在我们之前的讨论当中，得到了其中一个伏安特性曲线，见下图：

从上图我们可以看出来，当加上反向电压的时候，半导体一侧的势垒高度会变高，随着反向电压的逐渐增大，从半导体一侧流到金属的电子基本可以忽略不计，而由于金属一侧的势垒高度基本不随外加电压的变化而变化，且反向电流的值十分的小，所以得到上图的伏安特性是基本处于一个截止的状态。但是实际上却并不是如此的，实验表明，如下图：

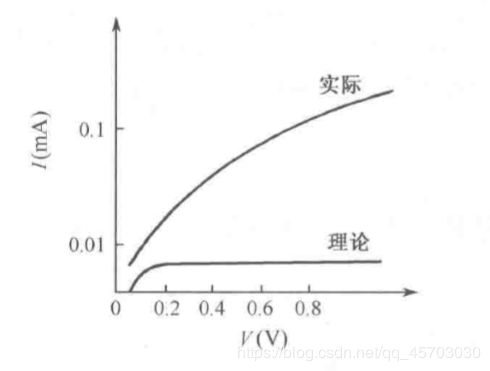
由图中我们可以得到实际上的电流变化是挺大的，这究竟是为什么呢？在此，我们讨论两个原因：镜像力和隧道效应

镜像力的影响
在金属——真空系统中，一个在金属外的电子，要在金属表面感应出正电荷，同时电子要收到正电荷的吸引。若电子距金属表面的距离为x，则它与感应正电荷之间的吸引力，相当于该电子与位于(-x)处的等量正电荷之间的吸引力，这个正电荷被称为镜像电荷，这个吸引力被称为镜像力。**（其中涉及到了许多的数值运算，在这次的博客当中我还未理解，抱歉！)**因此，这里我们直接给出我们的最后的结论分析。

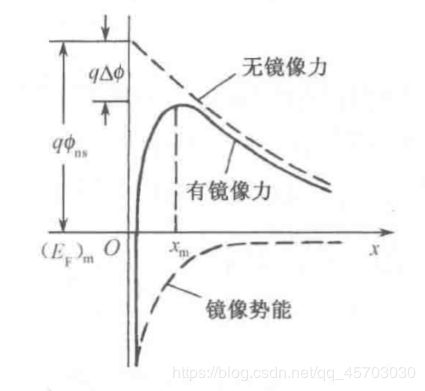
上图为有镜像力情况下的能级图表示

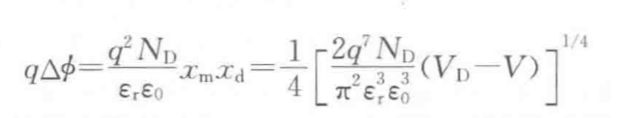
上图为势垒的下降度

从上式可以看出，镜像力所引起的势垒降低，是得在反向电压很大的情况下才显得明显；因此，由于势垒高度的下降十分明显则会反过去显著地影响到JsT和JsD的值，最终的效果则会使得反向电流不再处于饱和状态。

隧道效应的影响

根据隧道效应原理，能量低于势垒顶的电子有一定几率可以穿过这个势垒，穿透的概率与电子的能量和势垒的宽度有关；我们可以做这样的简化，对于一定能量的电子，存在一个临界势垒厚度Xc；若势垒厚度大于Xc，则电子完全不能穿过势垒；而如果势垒厚度小于Xc，则势垒对于电子而言完全透明，电子可以直接通过它，而不必越过势垒高度，也即势垒高度下降了。

上图是隧道效应所引起的势垒高度下降

综上，隧道效应所引起的势垒高度的下降也是与外加电压有关，外加电压越大，势垒高度下降得越多，基本与镜像力所导致得结果差不多。