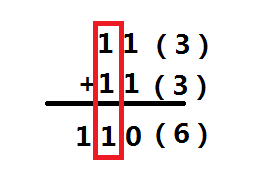FPGA从入门到精通(5) - 进位链
所使用EDA软件：VIVADO2019.1.3
FPGA型号：xc7a35tcsg325-2
看完这篇文章你将收获以下内容：
-
理解什么是加法器，内容包括半加器，全加器，多位加法器。
-
联系多位加法器来理解XILINX FPGA进位链的结构以及功能。
在讲加法器之前，我们先来看个有关二进制加法的例子
我们先关注两个1位二进制数进行相加的情况，它最后只有4中结果（图1）。0+0=0，0+1=1，1+0=0，1+1=10
标题图1：1位二进制数进行相加
我们可以观察得到以下3点：
-
两个加数都为0，相加的结果为0。
-
两个加数1个为0，另一个为1时，它们相加的结果为1。
-
两个加数都为1时，当前位的结果会为0，但它会给下一位进1，所以最后结果为10。
求当前输出位的结果，我们会用到数电中的异或逻辑，逻辑符号为⊕。
求当前进位的结果，我们会用到数电中的与逻辑，逻辑符号位·。
假设两个加数分别为A,B 。相加后，当前位的结果为S，是否产生进位用C来描述。
那么我们可以得出：
-
S=A⊕B
-
C=A·B
对两个输入数据位(A、B)相加，输出一个结果位(S)和进位(C)，没有进位输入的加法器电路我们将它称为半加器（图2）。上面的例子就是为了半加器中A,B,S,C是啥，以及他们之间的关系。千万别被半加器这个高大上的名字吓到，其实它就是拿来实现一个最最简单的二进制加法功能。
标图2：半加器符号题
接下来我们看一个2位二进制加法的例子（图3）
图3：2位二进制加法标题
对于第1位（从右往左）的1+1，由上面半加器的内容可知它相加后结果位(S1)为0，产生进位(COUT1)1。但是对于第2位的1+1来说（图3红框部分），它还需要接收由低位产生进位，才能计算当前位的结果位。多位二进制加法与十进制加法的规律是相似的，我们只需要将当前位相加，再加上低位的进位即为结果位，即1+1+1=1⊕1⊕1=1（从左往右计算，先算1⊕1=0，再算0⊕1=1）。如果当前的两个加数与进位里一共有两个或两个以上的1，那么它也会产生进位。
在第2位中我们用A2,B2,CIN2,S2,C2来分别表达两个加数，来自低位的进位，当前位的结果，当前位的进位,那么我们将得出：
-
S2=A2⊕B2⊕CIN2=1⊕1⊕1=1
-
C2=A2·B2+A2·CIN2+B2·CIN2+A2·B2·CIN2=A2·B2+A2·CIN2+B2·CIN2=1+1+1=1（注意这里的“+”指的是或操作）
-
同时C2也可以这样描述，C2=A2·B2+CIN2·(A2⊕B2),其实就是为了保证A2,B2,CIN2中有两个或两个以上的1。
在第3位中，两个加数A3=0,B3=0,来自低位的进位CIN3=1，用S3表示当前位的相加后的结果，C3表示当前位的进位我们可以得到
-
S3=A3⊕B3⊕CIN3=0⊕0⊕1=1
-
C3=A3·B3+A3·CIN3+B3·CIN3=0+0+0=0（注意这里的“+”代表着或）
由于最终没产生进位，第4位也没有相应的加数，最终的结果为{S3,S2,S1}=110
在数电中，我们用全加器(图4)来实现类似第2，3位这种加法操作。
图4：全加器符号标题
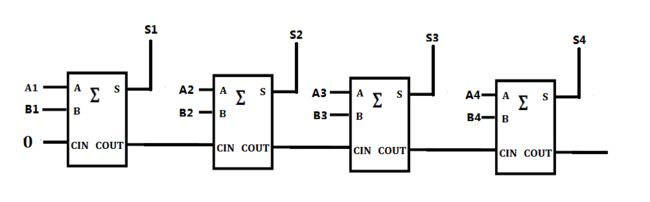
到这里可能有人会问，是不是每次做多位加法计算时，我的最低位都要用上个半加器。其实不然，事实上，全加器只不过是比半加器多了个来自低位进位的功能而已，我们只需要将CIN置0就可以了，就可以忽视它这一功能，即将全加器当作半加器来用，再与全加器级联即可做成多位加法器（图5）,A1~A4是一个加数的1到4位，B1~B4是另一个加数的1到4位，S4是结果的1到4位。（1是最低位，4是最高位）
标图5：用全加器级联成4位加法器题
那当我们将最第1个全加器的CIN置1，那么它与其他3个全加器级联将成为4位减法器（图6），A1~A4是被减数的1到4位，B1~B4是减数反码的1到4位，S4是结果的1到4位。（1是最低位，4是最高位）
图6：用全加器级联成4位减法器标题
此时的减法指的的补码形式的“减法”。不是指被减数 - 减数 ，而是指被减数的补码+减数负数形式的补码（即减数的反码+1）。所以图6中A[4:1]指的是被减数，B[4:1]指的是减数的反码，CIN1置1的目的就是为了减数的反码+1变成减数负数形式的补码。特别注意这里的A[4]、B[4]指的是符号位！！！。
拿0101-0010=0011（这里最高位（第4位）的0指的是符号位，0101的补码为0101，-0010的补码为1110，0011的补码为0011）作为个例子（图7）。最后的结果为0011（结果应为4位，忽略第5位，第5位“1”的作用就是为了告诉高位它要继续减，相当于第一位的CIN）。
图7：4位减法器的例子标题
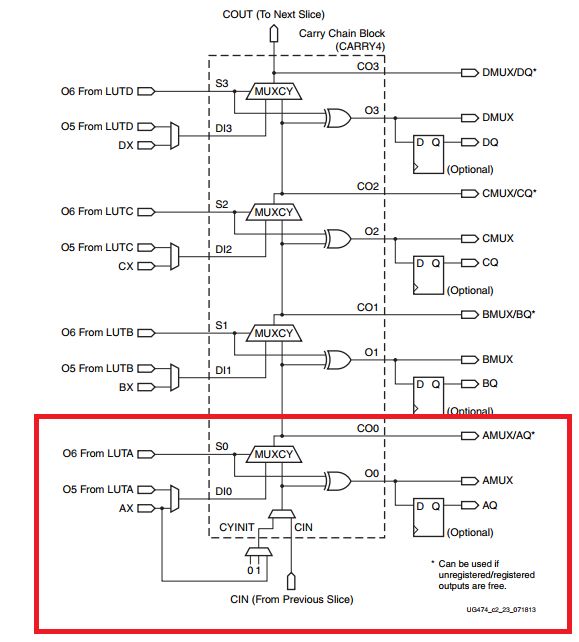
好的，哔哔了那么多，下面我开开始讲我们今天的主角进位链。首先我们看一下XILINX 7系中进位链的结构（图8）。
图8：XINLINX 7系中进位链的结构标题
红框框住的部分为它的1个基本单元（本质上是1个全加器）。
-
CIN=进位输入（当它在最低位时，置0做加法，置1做减法）
-
S0=A0⊕B0 （这里和全加器中的S有些区别），它来自LUTA的O6
-
O0=S0 ⊕CIN=A0⊕B0 ⊕CIN（这里的O才是全加器的S），它来自LUTA的O5或外面外部输入AX
-
DI0 = A0 或者 B0 （这里指的是两个加数中的一个，它的作用要配合S0）
-
AX 是预置数，这里我们不过多关注
我们知道产生进位的条件在A B以及 CIN中有两个或两个以上的1。
-
当S0=0时，有两种情况,即两个加数都为0和两个加数都为1。此时，MUXCY选择DI0作为数据输入，CO0的结果由DI0决定。因为S0=0时，DI0为0等价于A0，B0，COUT0都为0。DI0为1等价于A0，B0，COUT0都为1。
-
当S0=1时，即A0与B0中有1个为1。此时，MUXCY选择CIN0作为数据输入，CO0的结果由CIN0决定。因为S0=1时，A0与B0中只有1个1，还缺1个1才能进位，进位所需的那个1就看CIN1肯不肯施舍了。
然后我们看一下1个8位加法的例子（例1），综合后的结果如图9所示。
//以下是例1
module carrychain(
input [7:0] a,
input [7:0] b,
output[7:0] o
);
assign o=a+b;
endmodule
图9：例1综合后的原理图标题
图9我们可以看到
-
进位链1的CO[3]连到进位链2的CI，两者级联产生更大位宽的进位链。
-
两个加数的低四位异或后连入进位链1的S[3:0],两个加数的高四位异或后连入进位链2的S[3:0]。
-
其中一个加数低四位(a[3:0])连入进位链1的DIN[3:0],a[6:4]连到了进位链2的DIN[2:0]。此时进位链2的DIN[3]直接置0，因为我们输出位只有8位所以无需关注最高位进位(进位链2的CO3)，将DIN[3]置0来一来可以减小输入的翻转来降低功耗，二来可以减小输入数据的延迟不一致产生毛刺的概率。
-
进位链1 O[3:0]连到输出的低4位，进位链2的O[3:0]连到输出的高4位。
有关进位链的内容就大概说到这里，再补充两点。
-
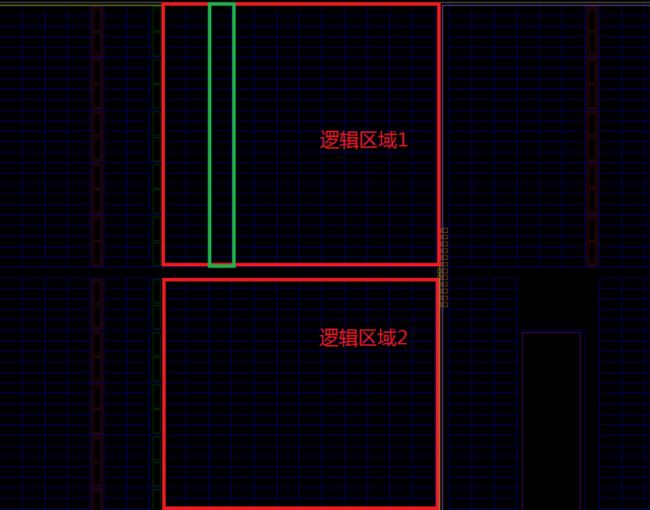
进位链级联数有限制，它取决于当前列SLICE的个数，而且不能跨逻辑区域。如图10所示，两个逻辑区域间是有条“楚河汉界”的，逻辑区域里进位链最大级数等于绿框中的SLICE的高度（如果是多位全加器的位宽就是SLICE的高度x4，因为1个SLICE里有4个级联的全加器）。
图10：最大进位链最大级联数示意标题
-
进位链级联数越多，造成的路径延迟就会越大，这样会让时序十分的紧张。所以在使用进位链时要综合考虑级联数与整个系统速率的关系。例如在设计位宽较大的计数器，可以选择用DSP替换，也可以选择将位宽分隔。（如32位计数器，可将它分成高16位，与低16位，低16位计数到16'hffff，高16位计数才+1）
好的本节就到这里，又到了一节一度的求赞求关注环节，谢谢老板们！！！
公众号关注 FPGA说，你的关注将引来更多的优质好文。
标题