统计学之三大相关性系数(pearson、spearman、kendall)
(转自 微信公众号克里克学苑)
三个相关性系数(pearson, spearman, kendall)反应的都是两个变量之间变化趋势的方向以及程度,其值范围为-1到+1,0表示两个变量不相关,正值表示正相关,负值表示负相关,值越大表示相关性越强。
1. person correlation coefficient(皮尔森相关性系数)
公式如下:
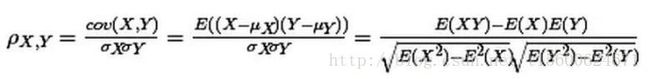
统计学之三大相关性系数(pearson、spearman、kendall)
重点关注第一个等号后面的公式,最后面的是推导计算,暂时不用管它们。看到没有,两个变量(X, Y)的皮尔森相关性系数(ρX,Y)等于它们之间的协方差cov(X,Y)除以它们各自标准差的乘积(σX, σY)。
公式的分母是变量的标准差,这就意味着计算皮尔森相关性系数时,变量的标准差不能为0(分母不能为0),也就是说你的两个变量中任何一个的值不能都是相同的。如果没有变化,用皮尔森相关系数是没办法算出这个变量与另一个变量之间是不是有相关性的。
就好比我们想研究人跑步的速度与心脏跳动的相关性,如果你无论跑多快,心跳都不变(即心跳这个变量的标准差为0),或者你心跳忽快忽慢的,却一直保持一个速度在跑(即跑步速度这个变量的标准差为0),那我们都无法通过皮尔森相关性系数的计算来判断心跳与跑步速度到底相不相关。
我们再拔高一点,来看个更具普遍性的例子吧,其中的计算我们使用广受欢迎的R语言来运行,如果你手边也装了R语言,可以一起来做做看:
假设你现在做了个生物学实验,喜得以下两个变量:
X1=c(1, 2, 3, 4, 5, 6)
Y1=c(0.3, 0.9, 2.7, 2, 3.5, 5)
X1<-c(1, 2, 3, 4, 5, 6)
Y1<-c(0.3, 0.9, 2.7, 2, 3.5, 5)
mean(X1) #平均值
[1] 3.5
mean(Y1)
[1] 2.4
var(X1) #方差
[1] 3.5
var(Y1)
[1] 2.976
sd(X1) #标准差
[1] 1.870829
sd(Y1)
[1] 1.725109
cov(X1,Y1) #协方差
[1] 3.06
cor(X1,Y1,method=”pearson”) #皮尔森相关性系数
[1] 0.9481367
其值在0.9以上,说明二者非常相关,比如验证了蛋白A表达量的变化,与蛋白B表达量的变化关系很大!拿到这种有统计学论证的结果你可能很开心。
然而,由于实验操作不慎或者处理数据不小心,得到了这样一个变量X2(1,1,1,1,1,1),那么计算X2与Y1之间的皮尔森相关性系数会发生什么呢?
X2<-c(1,1,1,1,1,1)
cor(X2,Y1,method=”pearson”)
[1] NA
Warning message:
In cor(X2, Y1, method = “pearson”) : the standard deviation is zero
R运行会得到一个缺失值(NA),并且代码给你提醒:标准差为零(自己试着计算下X2的标准差是多少),这时候明白上面说的意思了吧!也就是说,X2里面的取值根本没有任何波动,那它与Y1的相关性也就没法用这种方法来计算了。
此外,从上面的公式我们知道,皮尔森相关性系数是协方差与标准差的比值,所以它对数据是有比较高的要求的:
第一, 实验数据通常假设是成对的来自于正态分布的总体。为啥通常会假设为正态分布呢?因为我们在求皮尔森相关性系数以后,通常还会用t检验之类的方法来进行皮尔森相关性系数检验,而 t检验是基于数据呈正态分布的假设的。
统计学之三大相关性系数(pearson、spearman、kendall)
第二, 实验数据之间的差距不能太大,或者说皮尔森相关性系数受异常值的影响比较大。比如刚才心跳与跑步的例子,万一这个人的心脏不太好,跑到一定速度后承受不了,突发心脏病,那这时候我们会测到一个偏离正常值的心跳(过快或者过慢,甚至为0),如果我们把这个值也放进去进行相关性分析,它的存在会大大干扰计算的结果的。
2. spearman correlation coefficient(斯皮尔曼相关性系数)
斯皮尔曼相关性系数,通常也叫斯皮尔曼秩相关系数。“秩”,可以理解成就是一种顺序或者排序,那么它就是根据原始数据的排序位置进行求解,这种表征形式就没有了求皮尔森相关性系数时那些限制。下面来看一下它的计算公式:
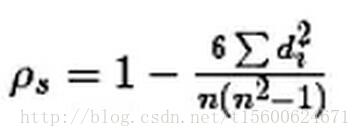
统计学之三大相关性系数(pearson、spearman、kendall)
计算过程就是:首先对两个变量(X, Y)的数据进行排序,然后记下排序以后的位置(X’, Y’),(X’, Y’)的值就称为秩次,秩次的差值就是上面公式中的di,n就是变量中数据的个数,最后带入公式就可求解结果。举个例子吧,假设我们实验的数据如下:
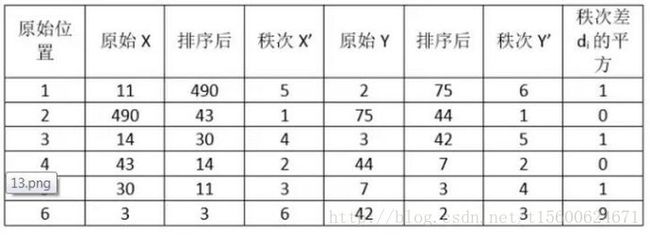
统计学之三大相关性系数(pearson、spearman、kendall)
带入公式,求得斯皮尔曼相关性系数:ρs= 1-6*(1+1+1+9)/6*35=0.657
也就是说,我们不用管X和Y这两个变量具体的值到底差了多少,只需要算一下它们每个值所处的排列位置的差值,就可以求出相关性系数了。这下理解起来是不是容易多了!还是用上面的数据,下面写下代码实现:
X<-c(11,490,14,43,30,3)
Y<-c(2,75,3,44,7,42)
cor(X,Y,method=”spearman”)
[1] 0.6571429
而且,即便在变量值没有变化的情况下,也不会出现像皮尔森系数那样分母为0而无法计算的情况。另外,即使出现异常值,由于异常值的秩次通常不会有明显的变化(比如过大或者过小,那要么排第一,要么排最后),所以对斯皮尔曼相关性系数的影响也非常小!
由于斯皮尔曼相关性系数没有那些数据条件要求,适用的范围就广多了。在我们生物实验数据分析中,尤其是在分析多组学交叉的数据中说明不同组学数据之间的相关性时,使用的频率很高。
3. kendall correlation coefficient(肯德尔相关性系数)
肯德尔相关性系数,又称肯德尔秩相关系数,它也是一种秩相关系数,不过它所计算的对象是分类变量。
分类变量可以理解成有类别的变量,可以分为
无序的,比如性别(男、女)、血型(A、B、O、AB);
有序的,比如肥胖等级(重度肥胖,中度肥胖、轻度肥胖、不肥胖)。
通常需要求相关性系数的都是有序分类变量。
举个例子。比如评委对选手的评分(优、中、差等),我们想看两个(或者多个)评委对几位选手的评价标准是否一致;或者医院的尿糖化验报告,想检验各个医院对尿糖的化验结果是否一致,这时候就可以使用肯德尔相关性系数进行衡量。
由于数据情况不同,求得肯德尔相关性系数的计算公式不一样,一般有3种计算公式,在这里就不繁琐地列出计算公式了,直接给出R语言的计算函数:
还是用cor函数求,这时候把method这个参数设成“kendall”,这时我们假设老师对选手的评价等级—3表示优,2表示中,1表示差:
X<-c(3,1,2,2,1,3)
Y<-c(1,2,3,2,1,1)
cor(X,Y,method=”kendall”)
[1] -0.2611165
这时候就可以理解为两位老师对选手们的看法是呈相反趋势的,不过这种相反的程度不很大。