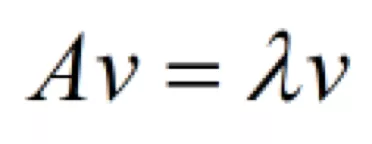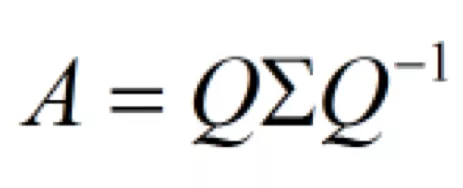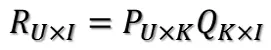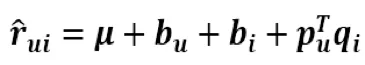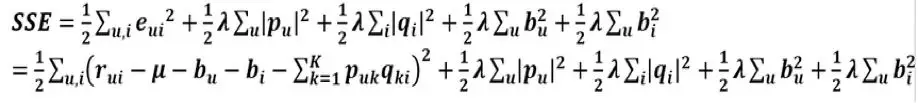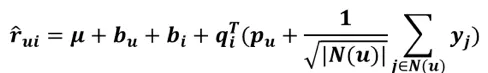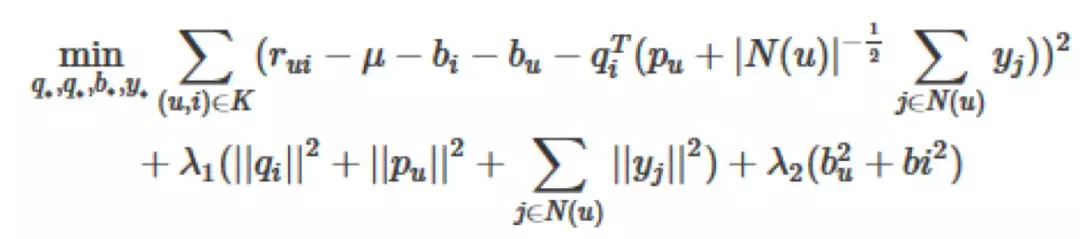推荐系统相关embedding:SVD、SVD++
继续讲embedding相关的一些东西,之前在公众号的地址:推荐系统相关embedding:SVD、SVD++
欢迎关注我的公众号,微信搜 algorithm_Tian 或者扫下面的二维码~
现在保持每周更新的频率,内容都是机器学习相关内容和读一些论文的笔记,欢迎一起讨论学习~
![]()
本篇主要想介绍一下基于推荐系统的embedding。为什么推荐系统也可以和embedding相关呢?这里面就涉及到了推荐系统中非常基础且应用非常广泛的SVD相关方法。为了让读者能够理解这其中的关系,我们从协同过滤概念讲起。
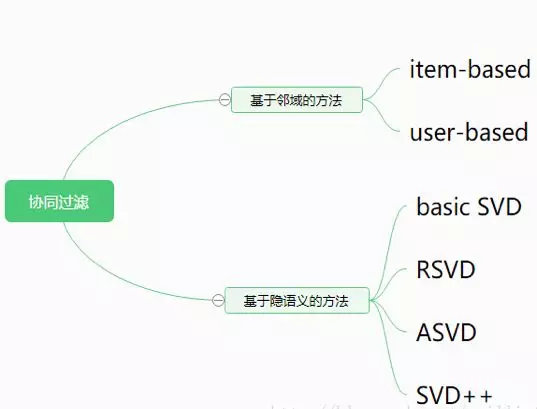
于是本篇主要从三个方面来讲:
1、协同过滤基础
1.1 user-based
1.2 item-based
2、特征值特征向量以及奇异值奇异向量
2.1 特征分解
2.2 奇异分解
3.基于SVD的方法及其扩展
3.1 basic SVD
3.2 RSVD
3.3 SVD++
1、协同过滤基础
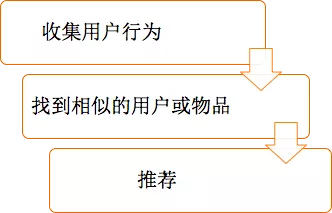
协同过滤算法是推荐算法的一个大分支,基本思想是给用户推荐与用户喜欢的物品相似的物品,或者推荐与用户相似用户喜欢的物品。
CF方法主要可以分为两类:基于邻域和基于隐语义。
协同过滤的主要流程如图:
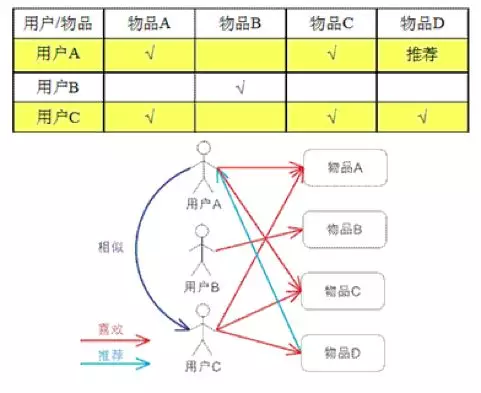
1.1 user-based
基于用户对物品的偏好找到相邻邻居用户,然后将邻居用户喜欢的推荐给当前用户。
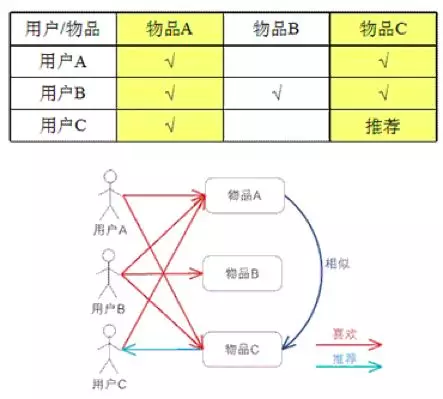
1.2 item-based
基于用户对物品的偏好找到相似的物品,然后根据用户的历史偏好,推荐相似的物品给他
2、特征值特征向量以及奇异值奇异向量
本篇最重要的部分就是SVD了对不对~但是,别着急,要讲协同过滤里基于SVD的方法,那么就要先了解特征分解和奇异值分解。所以插播一下很基础的特征分解和奇异值分解的概念。还记得这些内容的同学可以跳过不看~
2.1 特征分解
在这里,A是一个方阵,v是特征向量,这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量(实对称矩阵不同的特征值对应的特征向量是相互正交的)。特征值分解是将一个矩阵分解成下面的形式:
那么怎么通过第一个式子得到这个呢?如下图:
所以Q是矩阵A的特征向量组成的矩阵(列向量是特征向量),Σ是一个对角阵,每一个对角线上的元素就是一个特征值。
那么可以看到,在特征分解中,A必须是方阵,对不是方阵的矩阵不友好。但是大部分情况下,矩阵分解都是非方阵的矩阵分解,这个怎么办呢?于是就引出了奇异分解。
2.2 奇异分解
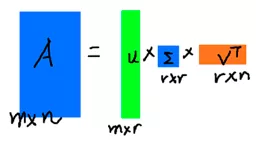
A能被分为这样三个矩阵的相乘的形式,左边是左奇异向量,右边是右奇异向量,中间是奇异值组成的对角矩阵。
在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r大的奇异值来近似描述矩阵
于是就有
奇异值和左右奇异向量的求解过程如下:
这里的σ就是奇异值,u是左奇异向量,v是右奇异向量。
3.基于SVD的方法及其扩展
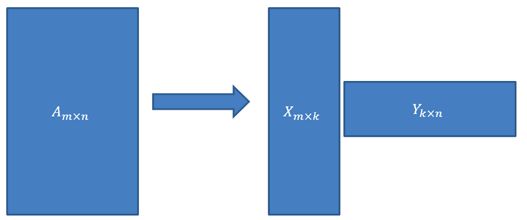
上面的奇异分解,为了书写方便,我们可以用两个矩阵来表示:
其中
也就是说,一个矩阵可以被分解成两个小矩阵相乘的形式。
那么协同过滤与奇异值分解的关系是什么呢?
基于隐语义的方法的基本思想是将用户和物品分别映射到各自的特征空间,然后通过两个特征向量的内积来判断用户对一个物品的喜好程度。
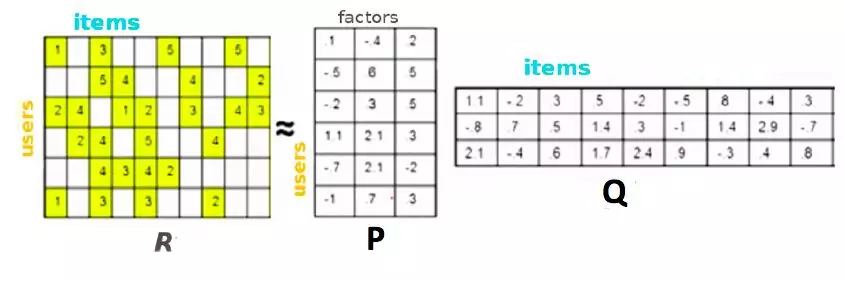
R是用户与item之间的评分矩阵,行数u表示用户数,列数i表示商品数。空白表示未知的打分。通过奇异值分解可以知道,评分矩阵R存在分解R=P*Q。
U表示用户数,I表示商品数。所以可以利用R中的已知评分训练P和Q使得P和Q相乘的结果最好地拟合已知的评分,那么未知的评分![]() 也就可以用P的某一行乘上Q的某一列得到
也就可以用P的某一行乘上Q的某一列得到
这是预测用户u对商品i的评分,它等于P矩阵的第u行乘上Q矩阵的第i列。(这里体现了embedding,可以把p的第u行视为第u个用户的embedding,q的第i列视为商品i的embedding)
在具体的模型中,向量每个维度的意义并不能人为给定,模型会自己通过最小化损失来学习这两个向量。
3.1 basic SVD
那么如何通过已知评分训练得到P和Q的具体数值呢?
误差为:
总的误差平方和:
为了求梯度后写起来简洁,于是加个1/2
接下来利用梯度下降法把SSE降到最小,那么P、Q就能最好地拟合R了。
利用梯度下降法可以求得SSE在Puk变量(也就是P矩阵的第u行第k列的值)处的梯度:
这就是basic SVD。可以目标函数中只有训练误差,就很容易导致过拟合问题。
3.2 RSVD
BasicSVD的公式容易过拟合,对于目标函数来说,P矩阵和Q矩阵中的所有值都是变量,这些变量在不知道哪个变量会带来过拟合的情况下,对所有变量都进行惩罚:因此,引入两个隐语义矩阵的正则项,得到RSVD:
由于用户对商品的打分不仅取决于用户和商品间的某种关系,还取决于用户和商品独有的性质,例如某些用户非常挑剔,对什么商品兴趣都不大;或是某个商品本身品质特别差,恶评如潮。为了模拟以上的情况,需要引入 baseline predictor,于是预测的评分![]() 变为:
变为:
加入的这两个变量在SSE式子中同样需要惩罚,那么SSE就变成了下面这样:
求梯度:
3.3 SVD++
这是SVD++的预测:
每个yj代表的是第j个商品的一个偏置embedding,N(u)代表的是用户u感兴趣的商品,有yj那一项代表的是用户u所有喜欢过的商品偏置向量加在一起以后除以系数之后的一个向量。所以y的整体大小是和item矩阵一样的一个矩阵。
某个用户对某个商品进行了浏览或点击(电影中是评分,因为评分说明他看过这部电影),那么这样的行为事实上蕴含了一定的信息,因此我们可以这样来理解问题:评分或浏览的行为从侧面反映了用户的喜好,可以将这样的反映通过隐式参数的形式体现在模型中,从而得到一个更为精细的模型,便是SVD++。收缩因子取集合大小的根号是一个经验公式,并没有理论依据。
加上各项正则之后,它的目标函数变为
梯度
那么基于协同过滤的embedding就介绍到这里啦~感谢各种博主深入浅出的讲解博文,这里面的一些图来自网络,参考了很多CSDN博主的文章,感谢各位大牛。
其实各个方法中可以和embedding沾边的真的很多。下篇文章准备和大家介绍一下知识图谱中涉及到embedding的link prediction。
有什么没有写明白的地方欢迎大家交流~
最后再来一波~
欢迎关注我的公众号,微信搜algorithm_Tian或者扫下面的二维码~
现在保持每周更新的频率,内容都是机器学习相关内容和读一些论文的笔记,欢迎一起讨论学习~
![]()