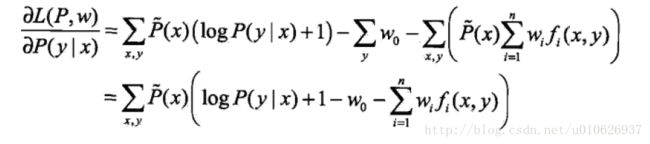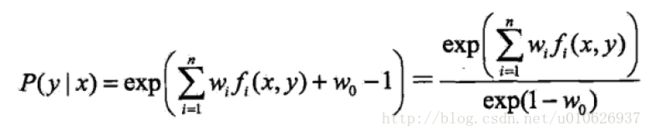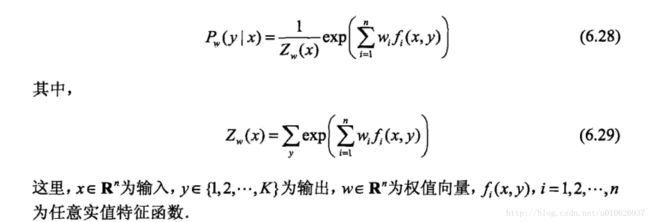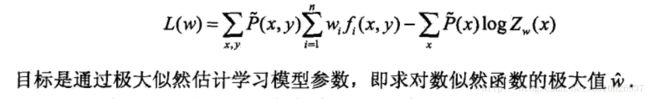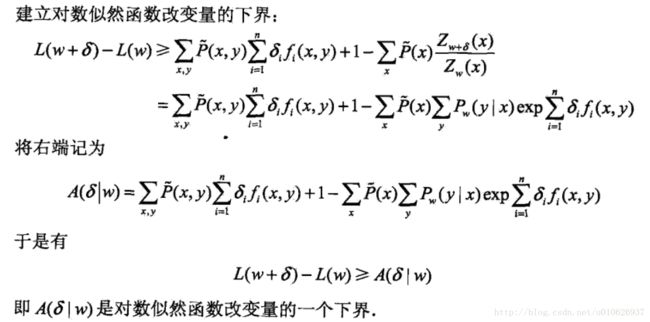《统计学习方法》笔记三---逻辑斯蒂（续）
续 最大熵模型
补充
最大熵模型的学习
最大熵模型的学习过程就是求解最大熵模型的过程，最大熵模型的学习可以形式化为约束最优化问题。
对于给定的训练数据集
以及特征函数
，最大熵模型的学习等价于约束最优化问题：
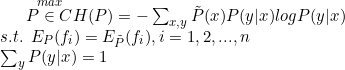
按照最后花问题的习惯，将求解最大值问题改写为等价的最小值问题：
求解约束最优化问题（6.14）~（6.16），所得出的解，就是最大熵模型学习的解，下面给出具体的推导。
这里，将约束最优化的原始问题转换为无约束最优化的对偶问题，通过来解对偶问题求解原始问题，
首先，引进拉格朗日乘子
，定义拉格朗日函数L(P,w):
PS:最后一个等号改为加号，误输入！最后一个等号改为加号，误输入！最后一个等号改为加号，误输入！
最优化的原始问题是
对偶问题是
由于拉格朗日函数L(P,w)是P的凸函数，原始问题的解与对偶问题的解释等价的。这样，就可以通过求解对偶问题来求解原始问题。
首先，求解对偶问题内部极小化问题
。是w的函数将其记作
称为对偶函数。同时将其解记作
具体地，求L(P,w)对P(y|x)的偏导数（突然觉得编辑数学公式好浪费时间，为了省时，以后比较繁琐的公式，均截图展示，见谅~）
令偏导数等于0,在
的情况下，解得
即：
下面化简该解，或者转换成另一种形式。由于
，所以，有：
则有以下：
仔细观察一下式子，可以看出点意思来~~~，有没有像点标准化的意思
称为规范化因子；
是特征函数；wi是特征的权值。由式（6.22）、式(6.23)表示的模型
就是最大熵模型。这里，w是最大熵模型中的参数向量。
之后，求解对偶问题外部的极大化问题
将其解记为
，即
这就是说，可以应用最优化算法求对偶函数的极大化，得到，用来表示
，这里，
是学习到的最优模型（最大熵模型），也就是说，最大熵模型的学习归结为对偶函数的极大化。
例题
（例题还是比较简单的，在此不再具体讲解。有问题可以留言）
极大似然估计
从以上最大熵模型学习中可以看出，最大熵模型是由式（6.22）、式（6.23）表示的条件概率分布。下面证明对偶函数的极大化等价于最大熵模型的极大似然估计。
已知训练数据的经验概率分布
,条件概率分布P(Y|X)的对数似然函数表示为
当条件概率分布P(y|x)是最大熵模型（6.22）和（6.23）时，对数似然函数
为：
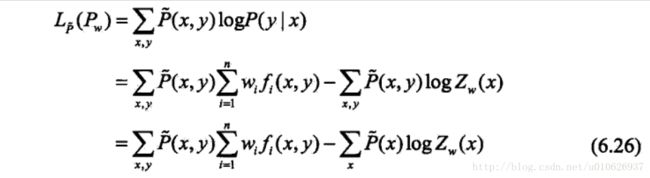
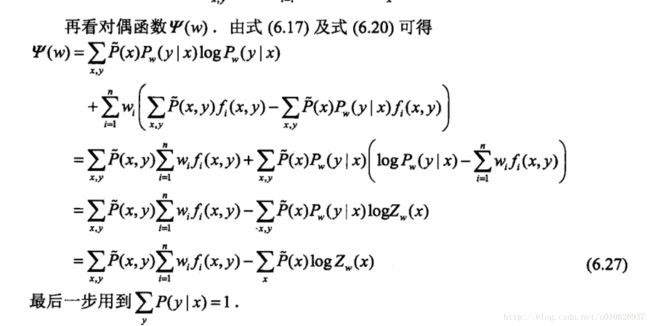
比较（6.26）和（6.27）可以得到：
既然对偶函数
等价于对数似然函数，于是证明了最大熵模型学习中的对偶函数极大化等价于最大熵模型的极大似然估计这一事实。
这样，最大熵模型的学习问题就转换为具体求解对数似然函数极大化或对偶函数极大化的问题。
可以将最大熵模型写成更加一般的形式。
最大熵模型与逻辑斯蒂回归模型有类似的形式，它们又称为对数线性模型（log linear model）模型学习就是在给定的训练数据条件下对模型进行极大化似然估计或正则化的极大似然估计。
模型学习的最优化算法
逻辑斯蒂回归模型、最大熵模型学习归结为以似然函数为目标函数的最优化问题，通常通过迭代算法求解。从最优化的观点 看，这时的目标函数具有很好的性质。他是光滑的凸函数，因此多种优化算法都适应，保证能够找到全局最优解，常用的方法有改进的迭代尺度算法、梯度下降算法、牛顿法或拟牛顿法。牛顿法或者拟牛顿法一般收敛速度更快。
改进的迭代尺度法
IIS的想法是：假设最大熵模型当前的参数向量是
，我们希望找到一个新的参数向量
，使得模型的对数似然函数值增大。如果能有这样的一种参数向量的更新方法
，那么就可以重复使用这个方法，直到找到对数似然函数的最大值。
如果能找到适当的
使下界
提高，那么对数似然函数也会提高。然而，函数
中的
是一个向量，含有多个变量，不易同时优化。IIS试图一次只优化其中一个变量
，而固定其他变量
为了达到这个目的，IIS进一步降低下界。具体地，IIS引进一个量
，
因为fi为二值函数，故表示所有特征在(x,y)出现的次数，这样可以改写为
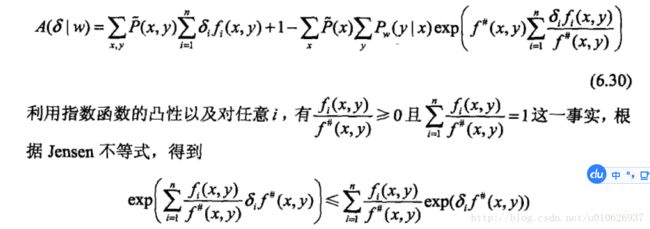
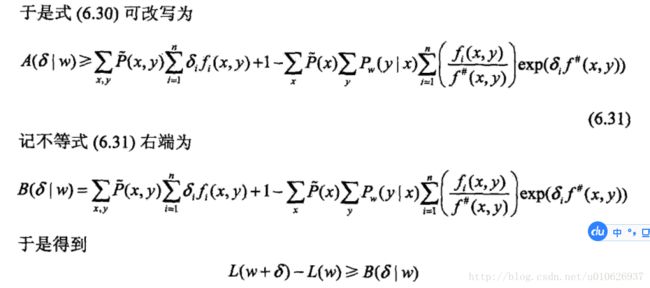
拟牛顿法
对于最大熵模型而言，
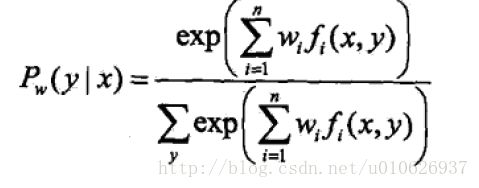
目标函数：
梯度：
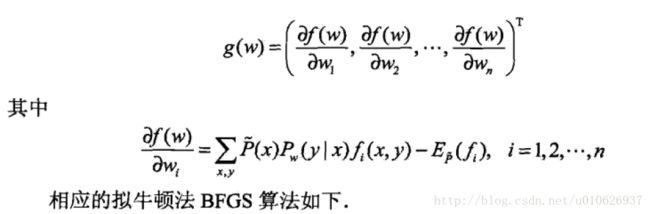
很多地方确实偷懒了，见谅呀。可以留言互相讨论问题~~~
《完》
（今天决定改一下落笔语~~~）
所谓的不平凡就是平凡的幂次方！
------ By Ada