贪心算法之最小堆实现霍夫曼编码

贪心算法之最小堆实现霍夫曼编码

实现之前需要学习的地方：

如果你不了解堆、堆的插入、堆的删除，可以先看下我前面几篇博客

http://blog.csdn.net/u011068702/article/details/52712634 最详细的最小堆构建、插入、删除的过程图解

http://blog.csdn.net/u011068702/article/details/52767187  

堆排序图片详解

http://blog.csdn.net/u011068702/article/details/52771173  堆的构建、堆的插入、堆的删除、堆排序

问题：

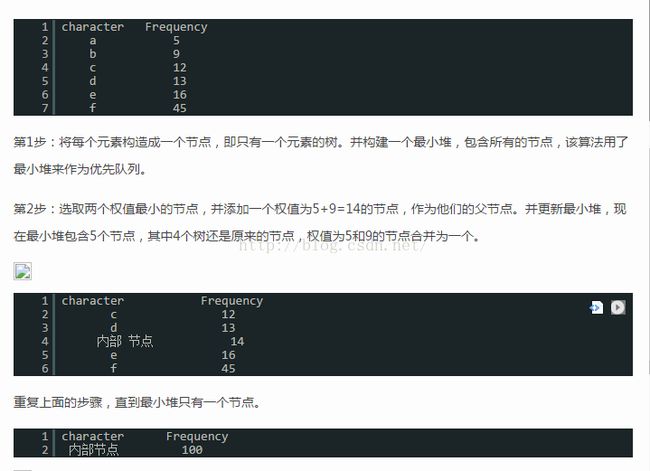
  哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%～90%之间。哈夫曼编码算法用字符在文件中出现的频率表来建立一个用0，1串表示各字符的最优表示方式。一个包含100,000个字符的文件，各字符出现频率不同，如下表所示。

有多种方式表示文件中的信息，若用0,1码表示字符的方法，即每个字符用唯一的一个0,1串表示。若采用定长编码表示，则需要3位表示一个字符，整个文件编码需要300,000位；若采用变长编码表示，给频率高的字符较短的编码；频率低的字符较长的编码，达到整体编码减少的目的，则整个文件编码需要（45×1+13×3+12×3+16×3+9×4+5×4）×1000=224,000位，由此可见，变长码比定长码方案好，总码长减小约25%。

     前缀码：对每一个字符规定一个0,1串作为其代码，并要求任一字符的代码都不是其他字符代码的前缀。这种编码称为前缀码。编码的前缀性质可以使译码方法非常简单；例如001011101可以唯一的分解为0,0,101,1101，因而其译码为aabe。

     译码过程需要方便的取出编码的前缀，因此需要表示前缀码的合适的数据结构。为此，可以用二叉树作为前缀码的数据结构：树叶表示给定字符；从树根到树叶的路径当作该字符的前缀码；代码中每一位的0或1分别作为指示某节点到左儿子或右儿子的“路标”。

哈夫曼树(Huffman Tree),又叫最优二叉树，

指的是对于一组具有确定权值的叶子结点的具有最小带权路径长度的二叉树。
(1)路劲(Path):从树中的一个结点到另一个结点之间的分支构成两个结点间的路径。
(2)路径长度(Path Length):路径上的分支树。
(3)树的路径长度(Path Length of Tree):从树的根结点到每个结点的路径长度之和。在结点数目相同的二叉树中，完全二叉树的路径长度最短。
(4)结点的权(Weight of  Node):在一些应用中，赋予树中结点的一个有实际意义的树。
(5)结点的带权路径长度(Weight Path Length of Node):从该结点到树的根结点的路径长度与该结点的权的乘积。
(6)树的带权路径长度(WPL):树中所有叶子结点的带权路径长度之和
构建霍夫曼树的步骤：
算法：输入是没有相同元素的字符数组(长度n)以及字符出现的频率，输出是哈夫曼树。

即假设有n个字符，则构造出得哈夫曼树有n个叶子结点。n个字符的权值(频率)分别设为w1,w2,…,wn,则哈夫曼树的构造规则为:

(1)将w1,w2,…,wn看成是有n棵树的森林(每棵树仅有一个结点);
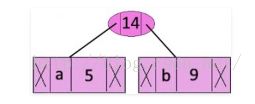
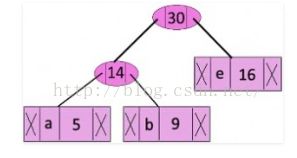
(2)在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
(3)从森林中删除选取的两棵树，并将新树加入森林;
(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。
用一个例子来了解该算法：

图片详解：

代码实现：

#include 
#include 

#define MAX_TREE_HT 100

// 一个霍夫曼树节点
struct MinHeapNode {
	char data;         // 输入的字符数组中的一个字符
	unsigned freq;	   // 字符出现的次数
	struct MinHeapNode *left, *right;
};

// 最小堆: 作为优先队列使用
struct MinHeap {
	unsigned size;     // 最小堆元素的个数
	unsigned capacity;  //最大容量
	struct MinHeapNode **array;
};

//初始化一个最小堆节点
struct MinHeapNode* newNode(char data, unsigned freq) {
	struct MinHeapNode* temp = (struct MinHeapNode*) malloc(sizeof(struct MinHeapNode));
	temp->left = temp->right = NULL;
	temp->data = data;
	temp->freq = freq;
	return temp;
};

// 创建一个容量为capacity 的最小堆
struct MinHeap* newMinHeap(unsigned capacity) {
	struct MinHeap* minHeap = (struct MinHeap*)malloc(sizeof(struct MinHeap));
	minHeap->size = 0;
	minHeap->capacity = capacity;
	struct MinHeapNode **array = (struct MinHeapNode **)malloc(minHeap->capacity * sizeof(struct MinHeapNode*));
	minHeap->array = array;
	return minHeap;
};

//  swap 两个堆节点
void swapMinHeapNode(struct MinHeapNode **a, struct MinHeapNode **b) {
	struct MinHeapNode* temp = *a;
	*a = *b;
	*b = temp;
}

//得到左孩子节点下标，默认第一个节点下标为0
int getLeftIndex(int index) {
	return ((index << 1) + 1);
}

//得到右孩子节点下标，默认第一个节点下标为0
int getRightIndex(int index) {
	return ((index << 1) + 2);
}

// 调整最小堆
void adjustMinHeap(struct MinHeap* minHeap, int index) {
	int less = index;
	int left = getLeftIndex(index);
	int right = getRightIndex(index);
	if (left < minHeap->size && minHeap->array[left]->freq < minHeap->array[less]->freq) {
		less = left;
	}
	if (right < minHeap->size && minHeap->array[right]->freq < minHeap->array[less]->freq) {
		less = right;
	}
//	if (less = index) {
//		return;
//	} else {
//		swapMinHeapNode(&minHeap->array[less], &minHeap->array[index]);
//		adjustMinHeap(minHeap, less);
//	}   或者你也可以写成下面那样
	if (less != index) {
		swapMinHeapNode(&minHeap->array[less], &minHeap->array[index]);
		adjustMinHeap(minHeap, less);	
	}
}

//检测堆的大小是否为1
int isSizeOne(struct MinHeap* minHeap) {
	return (minHeap->size == 1);
}

// 检测是否是叶子节点
int isLeaf(struct MinHeapNode* node) {
	return !(node->left) && !(node->right);
}

// 打印
void printArr(int arr[], int n)
{
    int i;
    for (i = 0; i < n; ++i)
        printf("%d", arr[i]);
    printf("\n");
}

//取得堆中最小的节点
struct MinHeapNode* extractMin(struct MinHeap* minHeap) {
	struct MinHeapNode* temp = minHeap->array[0];
	minHeap->array[0] = minHeap->array[minHeap->size-1];
	--minHeap->size;
	adjustMinHeap(minHeap, 0);
	return temp;
}

// 想最小堆中插入一个节点
void insertMinHeap(struct MinHeap* minHeap, struct MinHeapNode* minHeapNode) {
	++minHeap->size;
	int i = minHeap->size - 1;
	while (i && minHeapNode->freq < minHeap->array[(i-1) / 2]->freq) {
		minHeap->array[i] = minHeap->array[(i-1) / 2];
		i = (i-1) / 2;
	}
	minHeap->array[i] = minHeapNode;
}

//构建一个最小堆
void buildMinHeap(struct MinHeap* minHeap) {
	int index = minHeap->size - 1;
	int i;
	for (i = (index - 1) / 2; i >= 0; --i) {
		adjustMinHeap(minHeap, i);
	}
}

// 创建一个容量为 size的最小堆，并插入 data[] 中的元素到最小堆
struct MinHeap* createAndBuildMinHeap(char data[], int freq[], int size) {
    struct MinHeap* minHeap = newMinHeap(size);
	for (int i = 0; i < size; i++) {
		minHeap->array[i] = newNode(data[i],  freq[i]);
	}
	minHeap ->size = size;
	buildMinHeap(minHeap);
	return minHeap;
}

// 构建霍夫曼树
struct MinHeapNode* buildHuffmanTree(char data[], int freq[], int size) {
	struct MinHeapNode *left, *right, *top;
	// 第 1步 : 创建最小堆.
	struct MinHeap* minHeap = createAndBuildMinHeap(data, freq, size);
	//直到最小堆只有一个元素
	while (!isSizeOne(minHeap)) {
		// 第二步: 取到最小的两个元素
		left = extractMin(minHeap);
		right = extractMin(minHeap);
		// 第三步: 根据两个最小的节点，来创建一个新的内部节点
        // '$' 只是对内部节点的一个特殊标记，没有使用
		top = newNode('$', left->freq + right->freq);
		top->left = left;
		top->right = right;
		insertMinHeap(minHeap, top);
	}
	// 第四步: 根据两个最小的节点，来创建一个新的内部节点
	return extractMin(minHeap);
}

// 打印霍夫曼编码
void printCodes(struct MinHeapNode* root, int arr[], int top) {
	if (root->left) {
		arr[top] = 0;
		printCodes(root->left, arr, top + 1);		
	}
	if (root->right) {
		arr[top] = 1;
		printCodes(root->right, arr ,top + 1);
	}
	// 如果是叶子节点就打印
	if (isLeaf(root)) {
		printf("%c:", root->data);
		printArr(arr, top);
	} 
}


// 构建霍夫曼树，并遍历打印该霍夫曼树
void HuffmanCodes(char data[], int freq[], int size)
{
   //  构建霍夫曼树
   struct MinHeapNode* root = buildHuffmanTree(data, freq, size);
   // 打印构建好的霍夫曼树
   int arr[MAX_TREE_HT], top = 0;
   printCodes(root, arr, top);
}


int main() {
	char arr[] = {'a', 'b', 'c', 'd', 'e', 'f'};
    int freq[] = {5, 9, 12, 13, 16, 45};
//	int size = sizeof(arr)/sizeof(char);
	int size = sizeof(arr)/sizeof(arr[0]);
	HuffmanCodes(arr, freq, size);
	return 0;
}

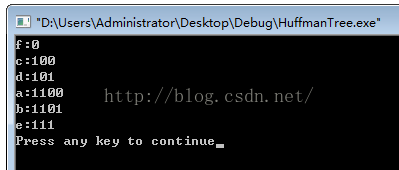
结果：

总结：

时间复杂度

O(nlogn)， 其中n是字符的数量。extractMin() 调用了 2*(n-1)次，extractMin()为log(n)的复杂度。