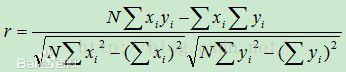R语言中的基本统计分析
(1)描述性分析
(2)频数表和列联表
(3)相关系数和协方差
(4)t检验
(5)非参数统计
具体的实现以上各个数据项
(1)描述性分析
若干用户贡献包都提供了计算描述性统计量的函数,其中包括Hmisc、pastecs psych。
summary()
apply(x,1/2,FUN)
sapply(x,FUN,Options) FUN=sum/mean,sd,var,min,max,quantitle,fivenum
vars <- c("mpg", "hp", "wt")
head(mtcars[,vars])
summary(mtcars[,vars])
mpg hp wt
Min. :10.40 Min. : 52.0 Min. :1.513
1st Qu.:15.43 1st Qu.: 96.5 1st Qu.:2.581
Median :19.20 Median :123.0 Median :3.325
Mean :20.09 Mean :146.7 Mean :3.217
3rd Qu.:22.80 3rd Qu.:180.0 3rd Qu.:3.610
Max. :33.90 Max. :335.0 Max. :5.424
newdata<-mtcars[,vars]
sapply(newdata,mean)
mpg hp wt
20.09062 146.68750 3.21725
> sapply(newdata,sum)
mpg hp wt
642.900 4694.000 102.952
> sapply(newdata,median)
mpg hp wt
19.200 123.000 3.325
> sapply(newdata,quantilt)
Error in match.fun(FUN) : object 'quantilt' not found
> sapply(newdata,quantile)
mpg hp wt
0% 10.400 52.0 1.51300
25% 15.425 96.5 2.58125
50% 19.200 123.0 3.32500
75% 22.800 180.0 3.61000
100% 33.900 335.0 5.42400
> sapply(newdata,median)
mpg hp wt
19.200 123.000 3.325
> sapply(newdata,fivenum)
mpg hp wt
[1,] 10.40 52 1.5130
[2,] 15.35 96 2.5425
[3,] 19.20 123 3.3250
[4,] 22.80 180 3.6500
[5,] 33.90 335 5.4240
使用其他用户提供的包进行统计分析的功能
library(Hmisc)
describe(mtcars[,vars])
Hmisc包中的describe()函数可返回变量和观测的数量、缺失值和唯一值的数目、平均值、
分位数,以及五个最大的值和五个最小的值
3 Variables 32 Observations
-----------------------------------------------------------------------------
mpg
n missing unique Info Mean .05 .10 .25 .50
32 0 25 1 20.09 12.00 14.34 15.43 19.20
.75 .90 .95
22.80 30.09 31.30
lowest : 10.4 13.3 14.3 14.7 15.0, highest: 26.0 27.3 30.4 32.4 33.9
-----------------------------------------------------------------------------
hp
n missing unique Info Mean .05 .10 .25 .50
32 0 22 1 146.7 63.65 66.00 96.50 123.00
.75 .90 .95
180.00 243.50 253.55
lowest : 52 62 65 66 91, highest: 215 230 245 264 335
-----------------------------------------------------------------------------
wt
n missing unique Info Mean .05 .10 .25 .50
32 0 29 1 3.217 1.736 1.956 2.581 3.325
.75 .90 .95
3.610 4.048 5.293
lowest : 1.513 1.615 1.835 1.935 2.140
highest: 3.845 4.070 5.250 5.345 5.424
-----------------------------------------------------------------------------
library(psych)
describe(mtcars[vars])
二、分组统计
aggregate(x,by=list(name=列,name=列),FUN)
有缺点就是,每次只能使用一个统计函数
aggregate(mtcars[vars], by = list(am = mtcars$am), mean)
aggregate(mtcars[vars], by = list(am = mtcars$am), sd)
am mpg hp wt
1 0 17.14737 160.2632 3.768895
2 1 24.39231 126.8462 2.411000
by(data,INDICES,FUN) 可以返回多个统计值
其中data是一个数据框或矩阵,INDICES是一个因子或因子组成的列表,定义了分组,FUN是任意函数
by(newdata$mpg, mtcars$am, dstats)
mtcars$am: 0
mean sd
17.147368 3.833966
---------------------------------------------------------
mtcars$am: 1
mean sd
24.392308 6.166504
doBy包和psych包也提供了分组计算描述性统计量的函数
library(doBy)
mystats <- function(x, na.omit = FALSE) {
if (na.omit)
x <- x[!is.na(x)]
m <- mean(x)
n <- length(x)
s <- sd(x)
skew <- sum((x - m)^3/s^3)/n
kurt <- sum((x - m)^4/s^4)/n - 3
return(c(n = n, mean = m, stdev = s, skew = skew, kurtosis = kurt))
}
summaryBy(mpg + hp + wt ~ am, data = mtcars, FUN = mystats)
am mpg.n mpg.mean mpg.stdev mpg.skew mpg.kurtosis hp.n hp.mean hp.stdev
1 0 19 17.14737 3.833966 0.01395038 -0.8031783 19 160.2632 53.90820
2 1 13 24.39231 6.166504 0.05256118 -1.4553520 13 126.8462 84.06232
hp.skew hp.kurtosis wt.n wt.mean wt.stdev wt.skew wt.kurtosis
1 -0.01422519 -1.2096973 19 3.768895 0.7774001 0.9759294 0.1415676
2 1.35988586 0.5634635 13 2.411000 0.6169816 0.2103128 -1.1737358
其中的formula接受以下的格式:
在~左侧的变量是需要分析的数值型变量,而右侧的变量是类别型的分组变量。function
可为任何内建或用户自编的R函数。
library(psych)
describe.by(mtcars[vars], mtcars$am)
(2)频数表和列联表
1. 一维列联表
library(vcd)
mytable <- with(Arthritis, table(Improved))
mytable
prop.table(mytable)
prop.table(mytable)*100
2、二维列联表
mytable <- table(A,B)
mytable <- xtabs(~ Treatment+Improved, data=Arthritis)
mytable
Improved
Treatment None Some Marked
Placebo 29 7 7
Treated 13 7 21
margin.table(mytable, 1)
Treatment
Placebo Treated
43 41
prop.table(mytable, 1)
Improved
Treatment None Some Marked
Placebo 0.6744186 0.1627907 0.1627907
Treated 0.3170732 0.1707317 0.5121951
margin.table(mytable, 2)
Improved
None Some Marked
42 14 28
prop.table(mytable, 2)
Improved
Treatment None Some Marked
Placebo 0.6904762 0.5000000 0.2500000
Treated 0.3095238 0.5000000 0.7500000
prop.table(mytable)
Improved
Treatment None Some Marked
Placebo 0.34523810 0.08333333 0.08333333
Treated 0.15476190 0.08333333 0.25000000
addmargins(mytable)
Improved
Treatment None Some Marked Sum
Placebo 29 7 7 43
Treated 13 7 21 41
Sum 42 14 28 84
admargins(prop.table(mytable))
Improved
Treatment None Some Marked Sum
Placebo 0.34523810 0.08333333 0.08333333 0.51190476
Treated 0.15476190 0.08333333 0.25000000 0.48809524
Sum 0.50000000 0.16666667 0.33333333 1.00000000
addmargins(prop.table(mytable, 1), 2)
Improved
Treatment None Some Marked Sum
Placebo 0.6744186 0.1627907 0.1627907 1.0000000
Treated 0.3170732 0.1707317 0.5121951 1.0000000
addmargins(prop.table(mytable, 2), 1)
Improved
Treatment None Some Marked
Placebo 0.6904762 0.5000000 0.2500000
Treated 0.3095238 0.5000000 0.7500000
Sum 1.0000000 1.0000000 1.0000000
使用gmodels包中的CrossTable()函数是创建二维列联表的第三种方法
library(gmodels)
CrossTable(Arthritis$Treatment, Arthritis$Improved)
Cell Contents
|-------------------------|
| N |
| Chi-square contribution |
| N / Row Total |
| N / Col Total |
| N / Table Total |
|-------------------------|
Total Observations in Table: 84
| Arthritis$Improved
Arthritis$Treatment | None | Some | Marked | Row Total |
--------------------|-----------|-----------|-----------|-----------|
Placebo | 29 | 7 | 7 | 43 |
| 2.616 | 0.004 | 3.752 | |
| 0.674 | 0.163 | 0.163 | 0.512 |
| 0.690 | 0.500 | 0.250 | |
| 0.345 | 0.083 | 0.083 | |
--------------------|-----------|-----------|-----------|-----------|
Treated | 13 | 7 | 21 | 41 |
| 2.744 | 0.004 | 3.935 | |
| 0.317 | 0.171 | 0.512 | 0.488 |
| 0.310 | 0.500 | 0.750 | |
| 0.155 | 0.083 | 0.250 | |
--------------------|-----------|-----------|-----------|-----------|
Column Total | 42 | 14 | 28 | 84 |
| 0.500 | 0.167 | 0.333 | |
--------------------|-----------|-----------|-----------|-----------|
3、多维列联表
mytable <- xtabs(~ Treatment+Sex+Improved, data=Arthritis)
mytable
, , Improved = None
Sex
Treatment Female Male
Placebo 19 10
Treated 6 7
, , Improved = Some
Sex
Treatment Female Male
Placebo 7 0
Treated 5 2
, , Improved = Marked
Sex
Treatment Female Male
Placebo 6 1
Treated 16 5
ftable(mytable)
Improved None Some Marked
Treatment Sex
Placebo Female 19 7 6
Male 10 0 1
Treated Female 6 5 16
Male 7 2 5
三、独立性检验
chisq.test(table) 判断二个变量是否独立
(1)对于标称属性的X方检验(主要针对于列联表)
治疗的效果跟性别没有关系,跟治疗的方案有关系
可以P-value值得概率来判断是否推翻假设
p<0.01 二个变量的独立假设是不成立的
p>0.05 二个变量是独立的
library(vcd)
> mytable <- xtabs(~Treatment+Improved, data=Arthritis)
> chisq.test(mytable)
data: mytable
X-squared = 13.055, df = 2, p-value = 0.001463
> mytable <- xtabs(~Improved+Sex, data=Arthritis)
> chisq.test(mytable)
data: mytable
X-squared = 4.8407, df = 2, p-value = 0.08889
(2)Fisher精确检验(一般用于多维的检验)
mytable <- xtabs(~Treatment+Improved, data=Arthritis)
fisher.test(mytable)
Fisher's Exact Test for Count Data
data: mytable
p-value = 0.001393
alternative hypothesis: two.sided
(3) Cochran-Mantel—Haenszel检验
mytable <- xtabs(~Treatment+Improved+Sex, data=Arthritis)
mantelhaen.test(mytable)
mytable
Cochran-Mantel-Haenszel M^2 = 14.6323, df = 2, p-value = 0.0006647
其原假设是,两个名义变量在第三个变量的每一层中都是条件独立的
(4)二维列联表的相关性度量
vcd包中的assocstats()函数可以用来计算二维列联表的phi系数、列联系数和Cramer’s V系数
library(vcd)
mytable <- xtabs(~Treatment+Improved, data=Arthritis)
assocstats(mytable)
五、变量之间的相关性
Pearson积差相关系数衡量了两个定量变量之间的线性相关程度。Spearman等级相关系数则衡量分级定序变量之间的相关程度。Kendall’s Tau相关系数也是一种非参数的等级相关度量。
(1)括Pearson相关系数
cor()函数可以计算这三种相关系数,而cov()函数可用来计算协方差
默认参数为use="everything"和method="pearson"
states <- state.x77[, 1:6]
cov(states) 计算协方差矩阵 计算二二之间的相异度
cov(states)
Population Income Illiteracy Life Exp Murder HS Grad
Population 19931683.7588 571229.7796 292.8679592 -407.8424612 5663.523714 -3551.509551
Income 571229.7796 377573.3061 -163.7020408 280.6631837 -521.894286 3076.768980
Illiteracy 292.8680 -163.7020 0.3715306 -0.4815122 1.581776 -3.235469
Life Exp -407.8425 280.6632 -0.4815122 1.8020204 -3.869480 6.312685
Murder 5663.5237 -521.8943 1.5817755 -3.8694804 13.627465 -14.549616
HS Grad -3551.5096 3076.7690 -3.2354694 6.3126849 -14.549616 65.237894
cor(states) 计算二个变量之间的相似度
Population Income Illiteracy Life Exp Murder HS Grad
Population 1.00000000 0.2082276 0.1076224 -0.06805195 0.3436428 -0.09848975
Income 0.20822756 1.0000000 -0.4370752 0.34025534 -0.2300776 0.61993232
Illiteracy 0.10762237 -0.4370752 1.0000000 -0.58847793 0.7029752 -0.65718861
Life Exp -0.06805195 0.3402553 -0.5884779 1.00000000 -0.7808458 0.58221620
Murder 0.34364275 -0.2300776 0.7029752 -0.78084575 1.0000000 -0.48797102
HS Grad -0.09848975 0.6199323 -0.6571886 0.58221620 -0.4879710 1.00000000
cor(states, method="spearman")
cor(states, method="spearman")
Population Income Illiteracy Life Exp Murder HS Grad
Population 1.0000000 0.1246098 0.3130496 -0.1040171 0.3457401 -0.3833649
Income 0.1246098 1.0000000 -0.3145948 0.3241050 -0.2174623 0.5104809
Illiteracy 0.3130496 -0.3145948 1.0000000 -0.5553735 0.6723592 -0.6545396
Life Exp -0.1040171 0.3241050 -0.5553735 1.0000000 -0.7802406 0.5239410
Murder 0.3457401 -0.2174623 0.6723592 -0.7802406 1.0000000 -0.4367330
HS Grad -0.3833649 0.5104809 -0.6545396 0.5239410 -0.4367330 1.0000000
x <- states[, c("Population", "Income", "Illiteracy", "HS Grad")]
y <- states[, c("Life Exp", "Murder")]
cor(x, y)
Life Exp Murder
Population -0.06805195 0.3436428
Income 0.34025534 -0.2300776
Illiteracy -0.58847793 0.7029752
HS Grad 0.58221620 -0.4879710
polycor包中的hetcor()函数可以计算一种混合的相关矩阵,其中包括数值型变量Pearson积差相关系数、数值型变量和有序变量之间的多系列相关系数、有序变量之间的多分格相关系数以及二分变量之间的四分相关系数
如何验证一个数据框中各个属性是否相关?
cor.test(states[, 3], states[, 5]) 一次只能验证二个变量
一次验证多个属性是否相关(正相关,负相关,不相关)
library(psych)
corr.test(states, use = "complete")
六、独立样本的t检验
(1)t.test(y~x,data=)
y是数值向量,x是二元变量。
library(MASS)
t.test(Prob ~ So, data=UScrime)
Welch Two Sample t-test
data: Prob by So
t = -3.8954, df = 24.925, p-value = 0.0006506
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.03852569 -0.01187439
sample estimates:
mean in group 0 mean in group 1
0.03851265 0.06371269
0.0006506<0.01 所以可以推翻Prob 和So是独立的假设。
(2)非独立样本的t检验
library(MASS)
sapply(UScrime[c("U1", "U2")], function(x) (c(mean = mean(x),
sd = sd(x))))
U1 U2
mean 95.46809 33.97872
sd 18.02878 8.44545
with(UScrime, t.test(U1, U2, paired = TRUE))
data: U1 and U2
t = 32.4066, df = 46, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
57.67003 65.30870
sample estimates:
mean of the differences
61.48936
七、若两组数据独立,可以使用Wilcoxon秩和检验(更广为人知的名字是Mann–Whitney U检验)来评估观测是否是从相同的概率分布中抽得。
with(UScrime, by(Prob, So, median))
So: 0
[1] 0.038201
---------------------------------------------------------
So: 1
[1] 0.055552
wilcox.test(Prob ~ So, data=UScrime)
data: Prob by So
W = 81, p-value = 8.488e-05
alternative hypothesis: true location shift is not equal to 0
sapply(UScrime[c("U1", "U2")], median)
U1 U2
92 34
with(UScrime, wilcox.test(U1, U2, paired = TRUE))
data: U1 and U2
V = 1128, p-value = 2.464e-09
alternative hypothesis: true location shift is not equal to 0
(3)多于两组的比较
states <- as.data.frame(cbind(state.region, state.x77))
kruskal.test(Illiteracy ~ state.region, data=states)
请先安装npmc包。此包中的npmc()函数接受的输入为一个两
列的数据框,其中一列名为var(因变量),另一列名为class(分组变量)。
class <- state.region
var <- state.x77[, c("Illiteracy")]
mydata <- as.data.frame(cbind(class, var))
rm(class,var)
library(npmc)
summary(npmc(mydata), type = "BF")
aggregate(mydata, by = list(mydata$class), median)