数据结构系列（2）之 AVL 树

本文将主要讲解平衡二叉树中的 AVL 树，其中将重点讲解二叉树的重平衡方法，即左旋和右旋，以及 3+4 重构；这些方法都是后面要讲的 B 树，红黑树等 BBST 的重要基础；此外在看本文之前最好先看一下 二叉搜索树 ；

一、结构概述

前一篇博客里面讲了，二叉树同时具有向量的静态查找和列表的动态插入、删除等优点；当然这是在理想的状态下，但是当出现一些极端情况的时候，比如二叉树的右子树或者左子树全部为空，此时二叉树将退化为一个列表；所以为了避免这种情况就要使二叉树的左右子树尽量平衡，当然最好的情况是左右子树完全平衡，那么此时二叉树的查找效率就相当于二分查找；但实际上要维护二叉树的完全平衡非常困难，所以一般情况下我们都是维护二叉树的适度平衡，于是就产生了变种众多的 BBST（balance binary search tree）；

其中 AVL 树 就是其中一种，即 左右子树的高度差（平衡因子）< 2； 如图所示：

图中每个节点上方的数字就是平衡因子；

主体结构如下：

public class AVLTree2> extends BST {
  private AVLNode root;
  private class AVLNode extends BST.Node {
    private final T key;
    private int height;
    private AVLNode left;
    private AVLNode right;
    private AVLNode parent;
  }
}

二、重平衡

在我们使用 AVL 树 的时候，必然会有动态的插入和删除，同时平衡也会被打破，此时我们就需要一些旋转操作使得 AVL 树能够再次平衡；

1. 单旋

左旋（zag）

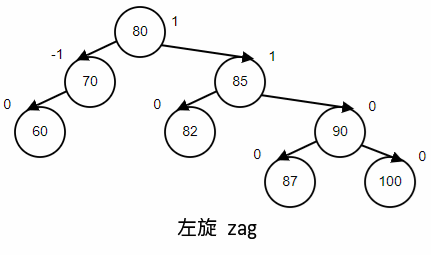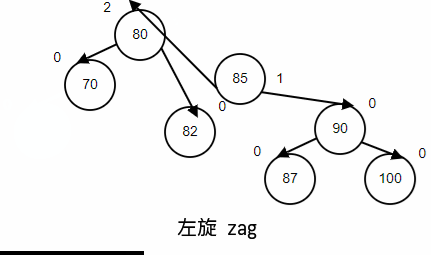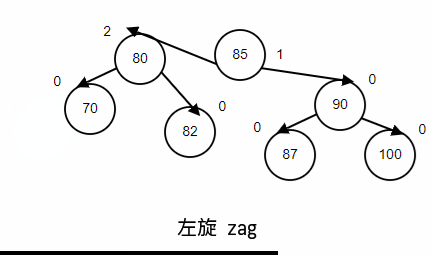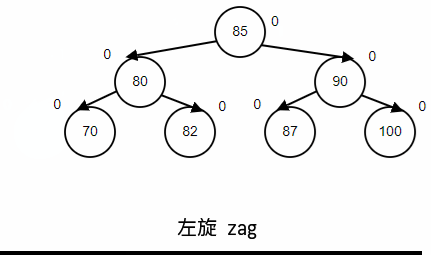
情景重现，顺序插入，70,80,85,60,82,90,87,100；最后删除60

实现：

private AVLNode rotateLeft(AVLNode x) {
  AVLNode y = x.right;
  y.parent = x.parent;

  x.right = y.left;
  if (x.right != null) {
    x.right.parent = x;
  }

  y.left = x;
  x.parent = y;

  if (y.parent != null) {
    if (x == x.parent.left) {
      y.parent.left = y;
    } else {
      y.parent.right = y;
    }
  } else {
    root = y;
  }

  updateHeight(x);
  updateHeight(y);
  return y;
}

右旋（zig）

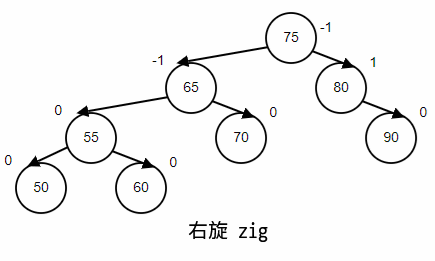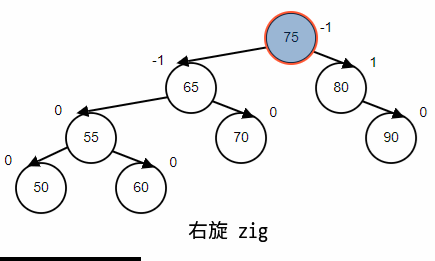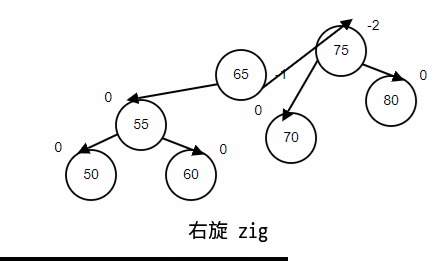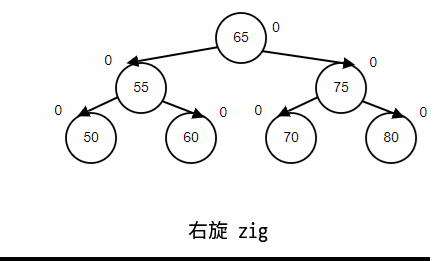
情景重现，顺序插入，65,75,80,90,70,55,60,50；最后删除90

实现：

private AVLNode rotateRight(AVLNode x) {
  AVLNode y = x.left;
  y.parent = x.parent;
  x.left = y.right;
  if (x.left != null) {
    x.left.parent = x;
  }

  y.right = x;
  x.parent = y;
  if (y.parent != null) {
    if (x == x.parent.left) {
      y.parent.left = y;
    } else {
      y.parent.right = y;
    }
  } else {
    root = y;
  }

  updateHeight(x);
  updateHeight(y);
  return y;
}

2. 双旋

对于以上左倾或者右倾的，自需要经过一次 zig 或者 zag 就可以恢复平衡；但是对于左倾右倾交叉的，则需要两次旋转；如图所示

对于以上情景的复现：

• 左图：顺序插入，70,80,90,60,100,85,82,87；最后删除60
• 中图：同上面左旋

3. （3+4）重构

当 AVL 树不在平衡的时候，任然还是一个 BST；也就是说不平衡的时候仍然有序，所以我们可以根据他的有序性直接构造出最终结果，而不是通过一次或者两次旋转；如图所示；

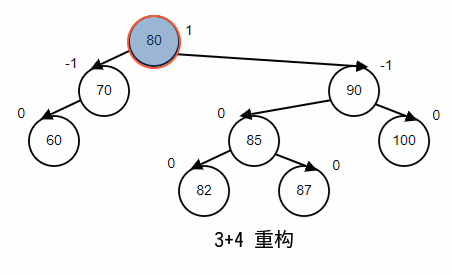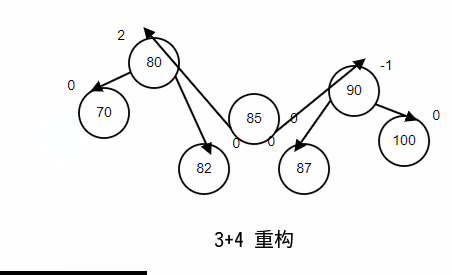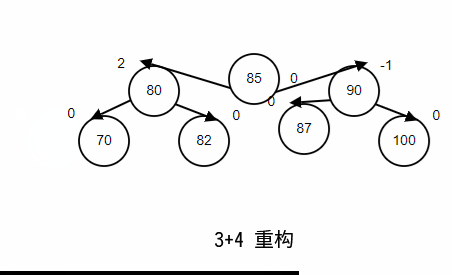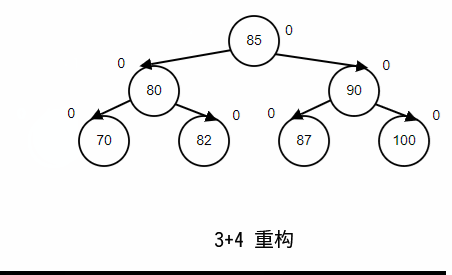
对于以上的各种重平衡方法，其 不变的都是树的顺序性，抓住这一点即使记不住旋转时候，节点之间关系的切换，画一个草图也能很快知道，应该如何调整；接下来我们就将使用上述的重平衡方法，继续研究 AVL 树使用过程中插入和删除的重平衡；

实现：

private AVLNode connect34(AVLNode a, AVLNode b, AVLNode c, AVLNode t0, AVLNode t1, AVLNode t2, AVLNode t3) {
  a.left = t0;
  if (t0 != null) t0.parent = a;
  a.right = t1;
  if (t1 != null) t1.parent = a;
  updateHeight(a);

  c.left = t2;
  if (t2 != null) t2.parent = c;
  c.right = t3;
  if (t3 != null) t3.parent = c;
  updateHeight(c);

  b.left = a;
  a.parent = b;
  b.right = c;
  c.parent = b;
  updateHeight(b);

  return b;
}

三、插入

@Override
public AVLNode insert(T key) {
  AVLNode node = (AVLNode) super.insert(key);
  updateHeight(node);

  // 插入节点，只需要调整一次，但是有可能是父亲节点或者祖父节点；
  for (AVLNode x = node; x != null; x = x.parent) {
    if (!isBalanced(x)) {
      balance(x);
      break;
    }
  }
  return node;
}

private AVLNode balance(AVLNode x) {
  if (balanceFactor(x) < -1) {
    if (balanceFactor(x.right) > 0) {
      x.right = rotateRight(x.right);
    }
    x = rotateLeft(x);
  } else if (balanceFactor(x) > 1) {
    if (balanceFactor(x.left) < 0) {
      x.left = rotateLeft(x.left);
    }
    x = rotateRight(x);
  }
  return x;
}

private int balanceFactor(AVLNode x) {
  return height(x.left) - height(x.right);
}

private boolean isBalanced(AVLNode x) {
  int i = balanceFactor(x);
  return i > -2 && i < 2;
}

具体插入算法就是找到为空的叶子节点，然后插入，详情可见 二叉搜索树 ；

四、删除

@Override
public AVLNode delete(T key) {
  AVLNode node = (AVLNode) super.delete(key);

  // 删除原本就矮的一边，使得重平衡后高度减一，不平衡向上传播
  // 使得祖父也不平衡，所以需要一次检查所有父亲节点
  for (AVLNode x = node; x != null; x = x.parent) {
    if (!isBalanced(x)) {
      balance(x);
    }
    updateHeight(x);
  }
  return node;
}

同样具体的删除算法也请参考 二叉搜索树 ；其思路就是：

• 先查找，如果该节点的其中一个或两个节点为空，直接令其后代代替；
• 如果不为空，则找到直接后继，然后交换位置，在删除；

五、重构

使用 3+4重构 的方式，重平衡；

private AVLNode balance34(AVLNode g) {
  AVLNode p = tallerChild(g);
  AVLNode v = tallerChild(p);

  if (balanceFactor(g) < -1) {
    if (balanceFactor(g.right) > 0) {
      /*
       *   O
       *    \
       *     O
       *   /
       *   O
       */
      return connect34(v, g, p, v.left, v.right, g.left, p.right);
    } else {
      /*
       *   O
       *    \
       *     O
       *      \
       *       O
       */
      return connect34(g, p, v, g.left, p.left, v.left, v.right);
    }
  } else if (balanceFactor(g) > 1) {
    if (balanceFactor(g.left) < 0) {
      /*
       *       O
       *     /
       *    O
       *     \
       *      O
       */
      return connect34(p, v, g, p.left, v.left, v.right, g.right);
    } else {
      /*
       *       O
       *      /
       *     O
       *    /
       *   O
       */
      return connect34(v, p, g, v.left, v.right, p.right, g.right);
    }
  }
  return g;
}

总结

• AVL 树同二叉搜索树相比无论查找，插入还是删除，其时间复杂度都只有 LOG(n) ;
• 但是从上述的讲解也可以看到插入和删除都需要旋转操作，成本仍然比较高；