磁感应强度
为了描述电场的分布,我们引入电场强度矢量\(\vec{E}\),同样,为了描述磁场的分布,我们也需要引入一个新的矢量,这个矢量就是磁感应强度\(\vec{B}\)。
两个电流元的磁相互作用力满足安培定律
\begin{equation*} \mathrm d\vec{F}_{12}=k\frac{I_2\mathrm d\vec{l}_2\times (I_1\mathrm d\vec{l}_1\times \hat{r_{12}})}{r_{12}^2}=\frac{\mu_0}{4\pi}\frac{I_2\mathrm d\vec{l}_2\times (I_1\mathrm d\vec{l}_1\times \hat{r_{12}})}{r_{12}^2} \end{equation*}
在国际单位制中,\(\frac{\mu_0}{4\pi}=10^{-7}\mathrm {N/A^2}\)。
元电流之间的安培力的表达式分成两项:
\begin{equation*} \mathrm d\vec{F}_{12}=I_2\mathrm d\vec{l}_2\times \mathrm d\vec{B} \end{equation*}
\begin{equation*} \mathrm d\vec{B}=\frac{\mu_0}{4\pi}\frac{I_1\mathrm d\vec{l}_1\times \hat{r_{12}}}{r_{12}^2} \end{equation*}
把电流元\(I_2 \mathrm d\vec{l} \_2\)看做试探电流元,则\(\mathrm d \vec{B}\)则为电流元\(I_1\mathrm d\vec{l} \_1\)的磁场在电流元\(I_2\mathrm d\vec{l} \_2\)所在位置处的磁感应强度。
整个回路1对电流元\(I_2\mathrm d\vec{l}_2\)的作用力为
\begin{equation*} \begin{split} \mathrm d\vec{F}_{2}=&\frac{\mu_0}{4\pi}\oint_{L_1}\frac{I_2\mathrm d\vec{l}_2\times (I_1\mathrm d\vec{l}_1\times \hat{r_{12}})}{r_{12}^2}=\frac{\mu_0}{4\pi}I_2d\vec{l}_2\times\mathrm \oint_{L_1}\frac{ I_1\mathrm d\vec{l}_1\times \hat{r_{12}}}{r_{12}^2} \\ =&I_2d\vec{l}_2\times \vec{B} \end{split} \end{equation*}
上式中
\begin{equation*} \vec{B}=\frac{\mu_0}{4\pi}\oint_{L_1}\frac{I_1\mathrm d\vec{l}_1\times \hat{r_{12}}}{r_{12}^2} \end{equation*}
即为闭合回路\(L_1\)的磁场在电流元\(I_2\mathrm d\vec{l}_2\)所在位置处的磁感应强度。
一个电流元在磁场中的受力
\begin{equation*} \mathrm d\vec{F}_{2}=I_2d\vec{l}_2\times \vec{B} \end{equation*}
这里的\(\vec{B}\)可以是电流产生的磁场,也可以是磁铁产生的磁场,或其他任何来源产生的磁场。
力的大小为
\begin{equation*} d{F}_{2}=I_2d{l}_2{B}\sin\theta \end{equation*}
其中,\(\theta\)为试探电流元方向与磁场方向的夹角。当两个方向平行或反平行时,\(\theta =0,\pi\),\(\mathrm dF_2=0\),当二者垂直时,试探电流元受力最大,\(d{F}_{2}=I_2d{l}_2{B}\),这样我们就可以确定空间任意一点磁感应强度的大小:
\begin{equation*} B=\frac{(d{F}_{2})_{max}}{I_2d{l}_2} \end{equation*}
磁场的方向由矢量叉乘的右手定则确定。
磁感应强度的单位为\(\mathrm{N/(A\cdot m)}\),这个单位有个专门的名称特斯拉,用\(\mathrm T\)表示,
\begin{equation*} 1\mathrm T=1 \mathrm{N/(A\cdot m)} \end{equation*}
另外一个广泛使用的单位是高斯,用\(\mathrm {Gs}\)表示,
\begin{equation*} 1\mathrm T=1 \mathrm {Gs} \end{equation*}
\begin{equation*} 1 \mathrm {Gs} =10^{-4}\mathrm T \end{equation*}
磁感应线可用来可视化磁场。
毕奥-萨伐尔定律
电流元和闭合载流回路产生在空间任意一点产生的磁场
\begin{equation*} \mathrm d\vec{B}=\frac{\mu_0}{4\pi}\frac{I\mathrm d\vec{l}\times \hat{r}}{r^2} \end{equation*}
\begin{equation*} \vec{B}=\frac{\mu_0}{4\pi}\oint_{L}\frac{I\mathrm d\vec{l}\times \hat{r}}{r^2} \end{equation*}
此两式正是毕奥-萨伐尔定律。
课堂练习:判断图中1-8各点的磁感应强度的方向和大小。
下面求解几种电流的磁场分布。
载流直导线的磁场
考虑一段直导线在场点\(P\) 处的磁感应强度。
载流直导线的磁场
根据毕奥-萨伐尔定律,任意电流元\(I\mathrm d\vec{l}\)产生的元磁场\(\mathrm d\vec{B}\)的方向一致(在点\(P\) 处的磁感应强度方向垂直纸面向里),因此总磁感应强度\(B\)的大小为\(\mathrm dB\)的代数和,
\begin{equation*} B=\int\mathrm dB=\frac{\mu_0}{4\pi}\int_{A_1}^{A_2}\frac{I\mathrm dl\sin\theta}{r^2} \end{equation*}
\(P\)点到导线距离为\(r_0\),由图可知,
\begin{equation*} l=-r_0\cot\theta \end{equation*}
\begin{equation*} r=\frac{r_0}{\sin\theta} \end{equation*}
所以
\begin{equation*} B=\frac{\mu_0I}{4\pi}\int_{A_1}^{A_2}\frac{\mathrm dl \sin\theta}{r^2}=\frac{\mu_0I}{4\pi r_0}\int_{\theta_1}^{\theta_2}\sin\theta\mathrm d\theta=\frac{\mu_0I}{4\pi r_0}(\cos\theta_1-\cos\theta_2) \end{equation*}
若导线为无限长(\(r_0 \ll l\)),\(\theta_1=0\),\(\theta_1=\pi\),则
\begin{equation*} B=\frac{\mu_0I}{2\pi r_0} \end{equation*}
即长载流导线周围的磁感应强度的大小与场点到导线的距离成反比。
长直导线周围的磁感应线是以导线为中心的同心圆,磁感应强度的方向由右手定则确定。
载流圆线圈轴线上的磁场
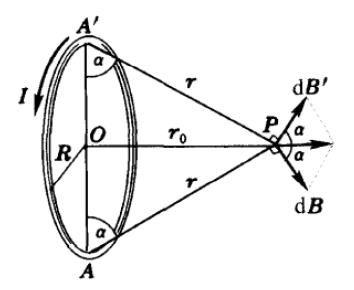
设圆线圈中心为\(O\),半径为\(R\),其上任意一点\(A\)处电流元在轴线上一点\(P\)处产生的磁场为\(\mathrm d\vec{B}\),线圈上与\(A\)点对称的点\(A'\)在点\(P\)处产生的磁场为\(\mathrm d\vec{B}'\),\(\mathrm d\vec{B}\)和\(\mathrm d\vec{B}'\)合成后沿\(OP\)方向,因此我们只需要计算电流元沿轴线方向的分量。对于整个圆线圈来说,在轴线上的磁场的总磁感应强度的方向沿轴线方向。
\begin{equation*} \begin{split} B=&\int \mathrm dB\cos\alpha=\frac{\mu_0I}{4\pi }\oint \frac{\mathrm dl}{r^2}\cos\alpha =\frac{\mu_0I}{4\pi r_0^2}\sin^2\alpha\cos\alpha\oint \mathrm dl \\ =&\frac{\mu_0IR}{2 r_0^2}\sin^2\alpha\cos\alpha \end{split} \end{equation*}
又
\begin{equation*} \sin\alpha=\frac{r_0}{\sqrt{r_0^2+R^2}} \end{equation*}
\begin{equation*} \cos\alpha=\frac{R}{\sqrt{r_0^2+R^2}} \end{equation*}
于是
\begin{equation*} B=\frac{\mu_0IR}{2 r_0^2}\sin^2\alpha\cos\alpha=\frac{\mu_0IR^2}{2(r_0^2+R^2)^{3/2}} \end{equation*}
在圆心处,\(r_0=0\)
\begin{equation*} B=\frac{\mu_0I}{2R} \end{equation*}
无限远处,\(r_0\gg R\)
\begin{equation*} B=\frac{\mu_0IR^2}{2r_0^{3/2}} \end{equation*}
亥姆霍兹线圈的磁场
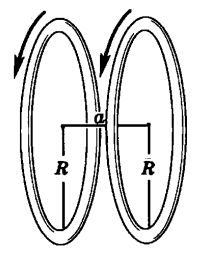
亥姆霍兹线圈(Helmholtz coil)是一种制造小范围区域均匀磁场的器件。由于亥姆霍兹线圈具有开敞性质,很容易地可以将其它仪器置入或移出,也可以直接做视觉观察,所以,是物理实验常使用的器件。如下图是一座装配了亥姆霍兹线圈的物理仪器。
下面我们讨论一下亥姆霍兹线圈中心轴线上的磁场。如下图所示,一对平行排列的相同的圆形线圈,通有同样的电流\(I\),且回绕方向一致,线圈的半径为\(R\),线圈相距\(a\)。
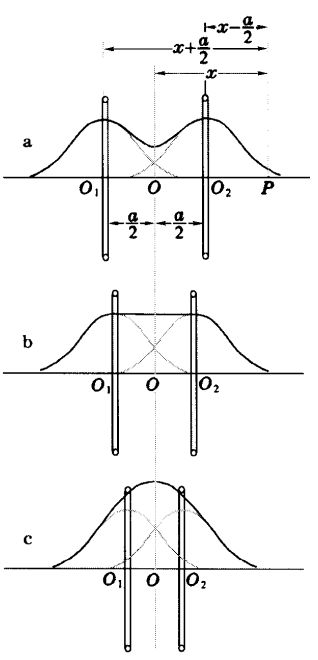
取线圈轴线上距离线圈等远处\(O\)点处为坐标原点,沿轴线建立\(O-x\)轴。则轴线上的磁场如下图所示。虚线为两线圈单独产生的磁场,实线为二者叠加之后的场。可以看出,当线圈间距\(a\)比较大时,\(O\)点处磁场为极小值,当线圈间距\(a\)比较小时,\(O\)点处磁场为极大值,因此当线圈间距\(a\)比较合适时,\(O\)点处接近均匀磁场。
设场点\(P\)的坐标为\(x\),则两线圈产生的磁场分别为
\begin{equation*} \vec{B}_1=\frac{\mu_0 IR^2}{2}\frac{1}{\left [R^2+(x+a/2)^2 \right ]^{3/2}}\vec{i} \end{equation*}
\begin{equation*} \vec{B}_2=\frac{\mu_0 IR^2}{2}\frac{1}{\left [R^2+(x-a/2)^2 \right ]^{3/2}}\vec{i} \end{equation*}
总磁场为
\begin{equation*} \vec{B}(x)=\vec{B}_1+\vec{B}_2=\frac{\mu_0 IR^2}{2}\left \{\frac{1}{\left [R^2+(x+a/2)^2 \right ]^{3/2}}+\frac{1}{\left [R^2+(x-a/2)^2 \right ]^{3/2}}\right \}\vec{i} \end{equation*}
将\(B(x)\)在\(x=0\)处做泰勒展开,
\begin{equation*} B(x)=B(0)+x\left( \frac{\mathrm dB(x)}{\mathrm dx} \right )_{x=0}+\frac{x^2}{2!}\left( \frac{\mathrm d^2B(x)}{\mathrm dx^2} \right )_{x=0}+\frac{x^3}{3!}\left( \frac{\mathrm d^3B(x)}{\mathrm dx^3} \right )_{x=0}+\frac{x^4}{4!}\left( \frac{\mathrm d^4B(x)}{\mathrm dx^4} \right )_{x=0}+O(x^4) \end{equation*}
由于\(B(x)\)是偶函数,\(B(x)=B(-x)\),故\(\left( \frac{\mathrm dB(x)}{\mathrm dx} \right )_{x=0}=0\),\(\left( \frac{\mathrm d^3B(x)}{\mathrm dx^3} \right )_{x=0}=0\),如果\(\left( \frac{\mathrm d^2B(x)}{\mathrm dx^2} \right )_{x=0}=0\),则
\begin{equation*} B(x)=B(0)+O(x^4) \end{equation*}
磁场最为均匀。
由\(\left( \frac{\mathrm d^2B(x)}{\mathrm dx^2} \right )_{x=0}=0\),得
\begin{equation*} a=R \end{equation*}
即两线圈的距离等于其半径。下图为亥姆霍兹线圈的示意图。
载流螺线管轴线上的磁场
螺线管是很细的导线密绕而成,因此可以把螺线管近似看成导体圆筒上套着许许多多圆电流。
沿轴线单位长度的圆电流的个数即为螺线管单位长度的匝数\(n\),电流强度为\(I\)。设螺线管半径为\(R\),总长度为\(L\),取圆筒中点为原点\(O\),圆筒轴线为\(x\)轴。长\(\mathrm dl\)内的电流在场点\(P\)处产生的磁感应强度为
\begin{equation*} \mathrm dB=\frac{\mu_0nIR^2}{2[(x-l)^2+R^2]^{3/2}}\mathrm dl \end{equation*}
因
\begin{equation*} x-l=R\cot\beta \end{equation*}
于是有
\begin{equation*} \mathrm dl=\frac{R}{\sin^2\beta}\mathrm d\beta \end{equation*}
磁感应强度
\begin{equation*} \begin{split} B=&\int\mathrm dB=\int_{-L/2}^{L/2}\frac{\mu_0nIR^2}{2[(x-l)^2+R^2]^{3/2}}\mathrm dl\\ =&\frac{\mu_0nI}{2}\int_{\beta_1}^{\beta_2}\sin\beta\mathrm d\beta=\frac{\mu_0nI}{2}(\cos\beta_1-\cos\beta_2) \end{split} \end{equation*}
其中,
\begin{equation*} \begin{cases} \cos\beta_1=&\frac{x+L/2}{\sqrt{R^2+(x+L/2)^2}}\\ \cos\beta_2=&\frac{L/2-x}{\sqrt{R^2+(L/2-x)^2}} \end{cases} \end{equation*}
对于无限长螺线管
\begin{equation*} B=\mu_0nI \end{equation*}
对于半无限长螺线管,端点处轴线上磁感应强度
\begin{equation*} B=\frac{\mu_0nI}{2} \end{equation*}
参考资料
- 赵凯华《电磁学》