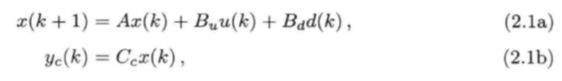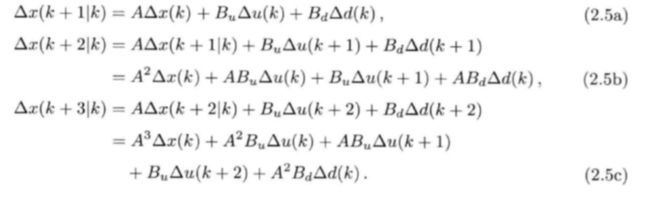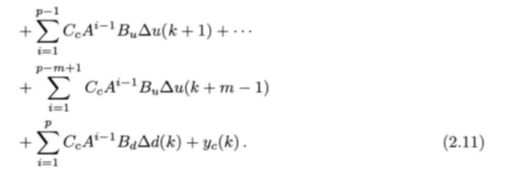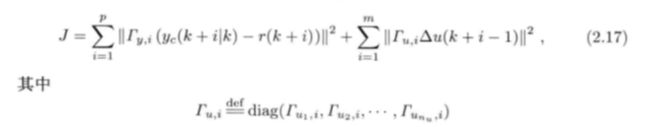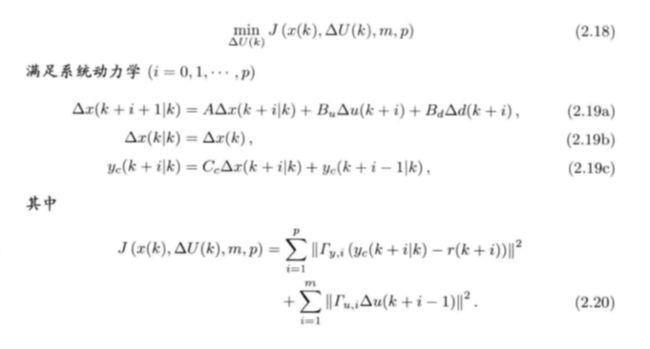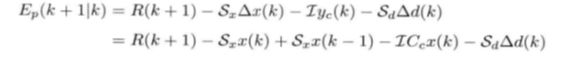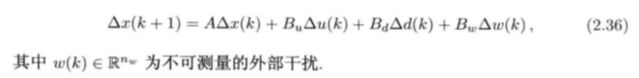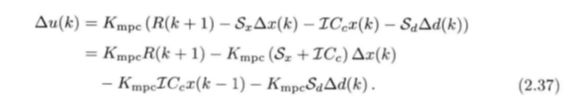MPC调节器
1.给定一个由状态空间法描述的离散系统:
MPC控制器与其他线性二次调节器(LQR)的区别就在于其可以很好的将系统动态约束纳入考虑。
采样周期Ts控制了算法的效率,太大会错过很多系统运行时的细节(扰动),太小又使得计算量变大。合适的取值应该取上升时刻Tr的5%-10%,或取调节时间的百分之十,在过渡时间内采样5-16次。
2.MPC的基本运行机理:
1)预测系统未来动态求解
2)优化问题
3)解的第一个元素作用于系统
4)滚动时域、重复进行
3.预测
按照运行机理的第一步,在给定系统动态方程下进行预测系统接下来的状态。对于2.1所描述的系统,将其写成增量形式:
增量形式系统动态方程
MPC可以天然地处理增量式问题,这有助于消除静态误差。MPC在每个采样时刻都在线的求解有限时域(p)一次开环最优问题。因此,在每个时刻我们都把最新的测量值作为初始条件,代入2.4即可预测未来系统动态。在预测的过程中,我们并不考虑系统真实的输出和状态,因为在控制信号输入前一切并未真正发生。同样,可测干扰在k 时刻之后也认为是不变的(在预测的过程中),即Δd(k + i) = 0。这样地去求解开环问题大大简便了计算。为了进一步提高计算速度,我们还在预测域p之外定义一个控制域m。一般m是小于等于p,当t>m时,控制量保持不变:Δu(k + i) = 0。M控制了优化问题独立变量个数,因此在牺牲一定自由度的基础上提高了计算快速性。
P的取值不能太小,否则系统可能由于参考输出r突然变化而无法做出反应。同样,p太大对扰动的反应会很慢。P的选取至少要大于系统开环响应的调节时间Ts,即此时偏差小于2%或5%。
M虽然越小越容易计算,但太小也会导致输出y一直达不到参考输入r。即使m=p,我们也只将第一个u作为真实输入,后续的u对实际输出曲线y的影响较小。故m一般取p或Ts的10%-20%,至少2-3个时间步。
当我们测量得到x(k)时,预测过程就开始了:
进一步,由输出方程(2 . 4b)可以预测k+l 至k+p 的被控输出:
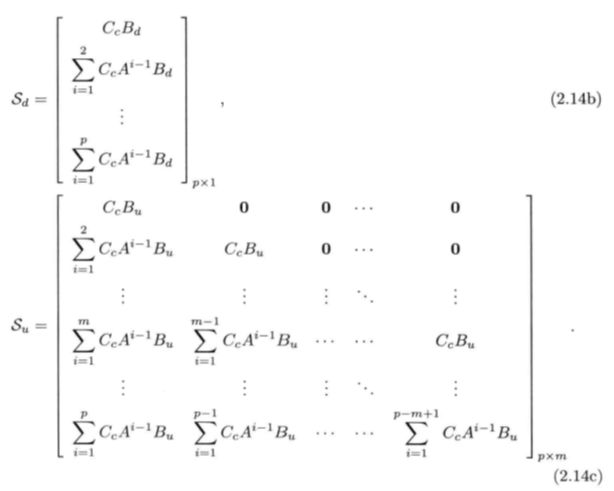
定义p 步预测输出向量和m 步输入向量如下:
矩阵下标表示的是矩阵中向量(或标量)的个数,不一定是矩阵的维数.例如,上式中, p × 1 仅表示马( k + Ilk )矩阵中Ye 的个数,当Ye 是向量时, px l
并不等于矩阵的维数.
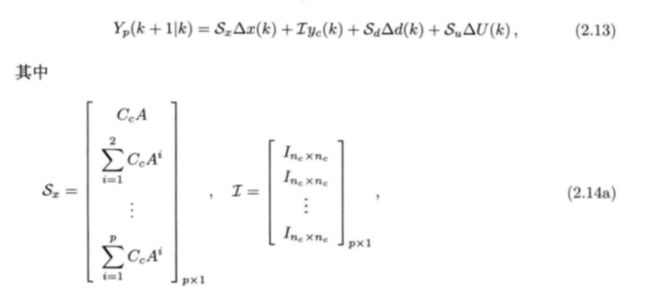
那么,对系统未来p 步预测的输出可以由下面的预测方程计算:
上式中Su 的下三角形式直接反映了系统在时间上的因果关系,即k+l 时刻的输
入对k 时刻的输出没有影响, k + 2 时刻的输入对k 和k+l 时刻的输出没有影响,
等等。
4.无约束预测控制
给定参考输入r,定义目标函数:
我们所要求解的问题:
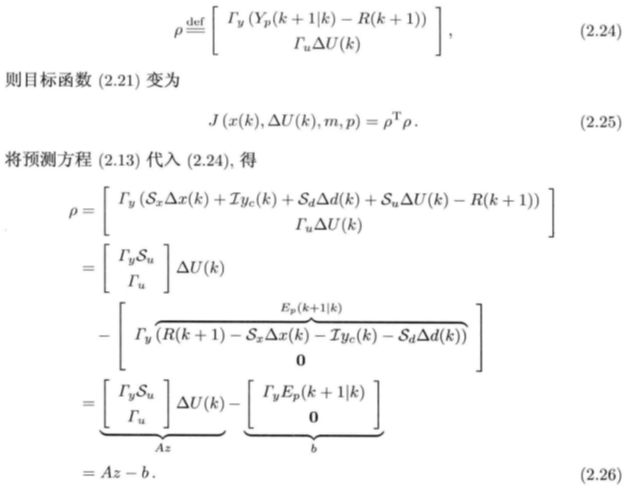
将(2.20)写成矩阵向量形式,则
定义辅助变量:
由此我们已经得到了控制序列U(k)。由于我们采用的预测模型是线性的,目标函数是二次型的,且没有考虑时域
硬约束,因此,可以得到优化问题的解析解,无须采用数佳方法求解。
U(k)中的元素是时间的函数,它以测量值y(k)为初始条件,并将第一个元素真实作用于系统:
由函数关系可知,U是当前测量值y(k)的函数:
![]()
但这里的控制序列是开环求解的,为了处理外部干扰和模型失配,只将第一个元素作为真实输入。假如将全部元素作为控制输入,y(k+1)之后的测量值将无法使用,使控制系统处于"离线"状态。因此最好的做法是,只用第一个控制输入,随后系统在控制信号作用下进入下一个时刻,得到新的测量值作为初始条件再次求解MPC问题,故也体现出MPC的反馈控制特性:
![]()
每个时刻的初始条件不同,MPC的目标函数也是处于动态变化过程中。虽然并不保证能求得全局最优解,但随着反复在线优化,整体控制效果要比传统的最优控制要好。
(2.35)中Ep(k + l l k)由(2.28 )在线计算.显然3 如果加权阵I'y 和几是与时间无关的常数,则Kmpc 可以由(2 . 34 )离线计算.在k+l 时刻,得到新的测量值x(k + 1),将由预测方程( 2. 13 )重新计算系统未来的输出,井且由(2.33)计算最优控制序列t:.U*(k + 1 ).最后,由预测控制基本原理中的"滚动时域、重复进行"的机制,给出无约束预测控制的算法如下:
下面仔细分析一下预测控制器(2.35)的结构.为此,将Yc(k) = Ccx(k)和t:. x(k) = x(k) - x(k - 1 )代入( 2.28 ),推导得:
上式中的各项具有以下解释:
(1)第一项是基于未来参考输入的前馈补偿
(2)第三项的是基于可测干扰的前馈补偿
(3)第二项+第四项是状态反馈补偿.值得注意的是,
这里的反馈补偿不仅用到了当前时刻的状态值,还用到了前一时刻的状态值.因此,预测控制(2.35 )具有"前馈-反馈"结构.这应该是在工业应用中的普遍结论"预测控制性能好"的控制理论解释。
需妥指出的是计算前馈控制量时用到了参考输入在预测时域内的所有值.因此,选择过长的预测时域可能会导致保守的控制动作。
5.闭环系统分析
在状态空间理论下,无约束MPC是可以达到渐进稳定的。
先推导预测控制闭环系统的表达式.将(2.lb )和(2.28)代入预测控制律(2. 35),得:
由此,闭环控制系统方程为:
若矩阵:
的所有特征值均位于单位圆内,则闭环系统( 2.3 8 )是名义渐近稳定的.因此,当我们完成无约束预测控制器设计后,需要核实矩阵的所有特征值是否在单位圆内。
同时,当系统满足渐进稳定时,MPC可以做到无静差跟踪。