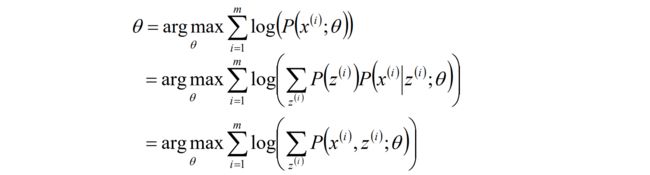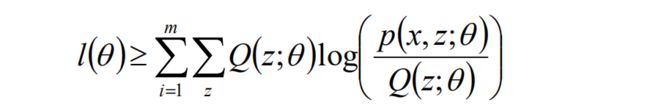01 EM算法 - 大纲 - 最大似然估计(MLE)、贝叶斯算法估计、最大后验概率估计(MAP)
K-means算法回顾:03 聚类算法 - K-means聚类
K-means算法,也称为k-均值聚类算法,是一种非常广泛使用的聚类算法之一。
假定输入样本为S=x1,x2,x3,...,xm,则算法步骤为:
1、选择初始的k个簇中心点μ1,μ2,...,μk;
2、将样本Xi标记为距离簇中心最近的簇: labeli;
3、迭代处理所有样本数据,计算出各个样本点所属的对应簇。
4、更新簇中心点坐标:μi;
5、重复上述三个操作(2~4),直到算法收敛。
算法收敛条件:迭代次数/簇中心变化率/MSE/MAE。
回到这个损失函数J(k,μ) ,我们的目的是将样本分成k个类,即样本中有k个隐藏的类别,而这k个类别是什么我不知道。我想找到这k个分类的坐标,利用这些坐标将样本集X进行划分。
EM的思想是,首先我先假定几个目标分类,但如何知道这些假定的分类是否正确?
我们使用样本的极大似然估计进行度量,如果找到的分类坐标能够让 P(预测结果=真实结果 | k) ,如果能够找到 k=y 让P(预测结果=真实结果)最大,那么说明y就是我们的最佳类别。而事实上我们知道,P(预测结果=真实结果)不仅仅依赖于分类的个数k=y,还依赖于分类点的初始值μ或等等其他因素。
我们就可以先固定k=y,然后调整μ的参数。在调整μ的过程中,我们可以获得一个更好的k值的选择。
最后重新指定k=ynew的作为初始值,再反复迭代计算 P(预测结果=真实结果 | k)的最大值,选择更好的y值。即我调整的是每一次K-means算法的初始聚类中心点,然后来找到最优的分类结果。
上述过程有几个难点:
第一,如何指定k=y? 是每种分类的划分都取相同的概率,还是不同分类结果有不同的概率?这种度量方式我们不知道。
第二,如何调正参数才能让最终的P(预测结果=真实结果|k,....)最大?
EM算法分为两步:
1、E - expectation 期望:估计出隐藏类别y的期望值。
2、M - Maximization 最大化:调整其他参数,使得在隐藏类别y的情况下能够达到最大值(极大似然估计),然后在其他参数确定的情况下,重新估计隐藏类别y的期望值。
....
四、EM算法引入
EM算法举例:
公司有男同事=[A,B,C],同时有很多漂亮的女职员=[小甲,小章,小乙]。(请勿对号入座)你迫切的怀疑这些男同事跟这些女职员有“问题”。为了科学的验证你的猜想,你进行了细致的观察。于是:
观察数据:
1、A,小甲、小乙一起出门了;
2、B,小甲、小章一起出门了;
3、B,小章、小乙一起出门了;
4、C,小乙一起出门了;
收集到了数据,你开始了神秘的EM计算。
初始化:你觉得三个同事一样帅,一样有钱,三个美女一样漂亮,每个人都可能跟每个人有关系。所以,每个男同事跟每个女职员“有问题”的概率都是1/3;
EM算法中的E步骤:
1、A跟小甲出去过了 1/2 * 1/3 = 1/6 次,跟小乙也出去了1/6次;
2、B跟小甲,小章也都出去了1/6次;
3、B跟小乙,小章又出去了1/6次;
4、C跟小乙出去了1/3次;
总计:
A跟小甲出去了1/6次,跟小乙也出去了1/6次 ;
B跟小甲,小乙出去了1/6次,跟小章出去了1/3次;
C跟小乙出去了1/3。
EM算法中的M步骤 - 你开始更新你的八卦:
A跟小甲,小乙有问题的概率都是1/6 / (1/6 + 1/6) = 1/2;
B跟小甲,小乙有问题的概率是1/6 / (1/6+1/6+1/6+1/6) = 1/4;
B跟小章有问题的概率是(1/6+1/6)/(1/6 * 4) = 1/2;
C跟小乙有问题的概率是1。
EM算法中的E步骤 - 然后你又开始根据最新的概率计算了。
1、A跟小甲出去了 1/2 * 1/2 = 1/4 次,跟小乙也出去 1/4 次;
2、B跟小甲出去了1/2 * 1/4 = 1/8 次, 跟小章出去了 1/2 * 1/2 = 1/4 次;
3、B跟小乙出去了1/2 * 1/4 = 1/8 次, 跟小章又出去了 1/2 * 1/2 = 1/4 次;
4、C跟小乙出去了1次;
EM算法中的M步骤 - 重新反思你的八卦:
A跟小甲,小乙有问题的概率都是1/4/ (1/4 + 1/4) = 1/2;
B跟小甲,小乙是 1/8 / (1/8 + 1/4 + 1/4 + 1/8) = 1/6 ;
B跟小章是 2/3 ;
C跟小乙的概率是1。
你继续计算,反思,总之,最后,你得到了真相。
通过上面的计算我们可以得知,EM算法实际上是一个不停迭代计算的过程,根据我们事先估计的先验概率A,得出一个结果B,再根据结果B,再计算得到结果A,然后反复直到这个过程收敛。
可以想象饭店的后方大厨,炒了两盘一样的菜,现在,菜炒好后从锅中倒入盘,不可能一下子就分配均匀,所以先往两盘中倒入,然后发现B盘菜少了,就从A中匀出一些,A少了,从B匀.....
五、EM算法概述
EM算法(Expectation Maximization Algorithm, 最大期望算法)是一种迭代类型的算法,是一种在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐藏变量。
1、EM算法流程:
1、初始化分布参数。
2、重复下列两个操作直到收敛:
E步骤:估计隐藏变量的概率分布期望函数;
M步骤:根据期望函数重新估计分布参数。
2、EM算法原理
给定的m个训练样本{x(1),x(2),...,x(m)},样本间独立,找出样本的模型参数θ,极大化模型分布的对数似然函数如下:
假定样本数据中存在隐含数据z={z(1),z(2),...,z(k)},此时极大化模型分布的对数似然函数如下:
期望回顾
对于离散型随机变量X,我们定义X的数学期望为:
X有i个取值x1~xi,分别乘以i个变量发生的概率pi,加和之后就得到了随机变量的期望EX;
若X是一个随机变量,g(X)是任意实函数,那么g(X)的数学期望Eg(X)为:
同理,函数乘以函数发生的概率,最后得到了整个函数集合的期望Eg(X);
证明:令Y=g(X),则Y仍然是一个离散型随机变量,设其可能的取值为yj,j=1,2,3……。于是:
根据期望的定义:
结论:复合函数g(x)的期望,就等同于每个xi取值出现的概率pi,乘以这个xi的在g(x)中的映射值g(xi);
补充知识:Jensen不等式
如果函数f为凸函数,那么存在下列公式:
拓展一下更多的点: 若θ1,...,θk≥0,θ1+....+θk=1;则
PS:如果我不是一个凸函数,是凹函数怎么办?
结论正好反一反即可。
2、EM算法原理(继续)
总结了期望和Jensen不等式的知识后,我们回过头继续推导EM算法原理。
Q(z) - 随机变量的分布。每一个取值对应的概率密度之和等于1;
令z的分布为Q(z;θ) ,并且Q(z;θ)≥0;那么有如下公式:
l(θ) 是我们一开始写到的极大似然估计的最大化的函数。
1~4的公式推导理解后,有这样一个问题:回到下面这个公式,即 f(E(X))和 E(f(x)) 分别怎么求?
一般情况下,z是隐含变量,我们不知道应该取多少合适。但有可能可以通过最后得到的这个公式对z进去求解。如果最后两步相等的话,我们就用公式的最后一步去替代l(θ),来求这个新公式的最大值。
问题来了,什么时候最后两步的公式相等?
根据不等式的性质,当下面式子中log内的随机变量为常数的时候,l(θ)和右边的式子取等号。
公式推导:
根据Jensen不等式的特性,当下列式子的值为常数的时候,l(θ)函数才能取等号。
最后结论:如果Q(z;θ) = p(z|x;θ) , l(θ)函数取得等号。
03 EM算法 - EM算法流程和直观案例