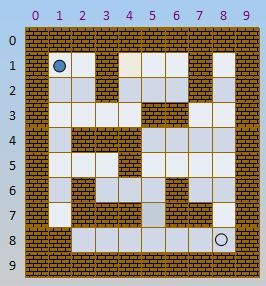
数据结构例程——迷宫问题（用队列）

　　本文针对数据结构基础系列网络课程(3)：栈和队列中第11课时队列的应用-迷宫问题。

例：求出从入口到出口的路径

代码：

#include 
#define MaxSize 100
#define M 8
#define N 8
int mg[M+2][N+2]=
{
    {1,1,1,1,1,1,1,1,1,1},
    {1,0,0,1,0,0,0,1,0,1},
    {1,0,0,1,0,0,0,1,0,1},
    {1,0,0,0,0,1,1,0,0,1},
    {1,0,1,1,1,0,0,0,0,1},
    {1,0,0,0,1,0,0,0,0,1},
    {1,0,1,0,0,0,1,0,0,1},
    {1,0,1,1,1,0,1,1,0,1},
    {1,1,0,0,0,0,0,0,0,1},
    {1,1,1,1,1,1,1,1,1,1}
};
typedef struct
{
    int i,j;            //方块的位置
    int pre;            //本路径中上一方块在队列中的下标
} Box;                  //方块类型
typedef struct
{
    Box data[MaxSize];
    int front,rear;     //队头指针和队尾指针
} QuType;               //定义顺序队类型

void print(QuType qu,int front) //从队列qu中输出路径
{
    int k=front,j,ns=0;
    printf("\n");
    do              //反向找到最短路径,将该路径上的方块的pre成员设置成-1
    {
        j=k;
        k=qu.data[k].pre;
        qu.data[j].pre=-1;
    }
    while (k!=0);
    printf("迷宫路径如下:\n");
    k=0;
    while (k<=front)  //正向搜索到pre为-1的方块,即构成正向的路径
    {
        if (qu.data[k].pre==-1)
        {
            ns++;
            printf("\t(%d,%d)",qu.data[k].i,qu.data[k].j);
            if (ns%5==0)
                printf("\n");   //每输出每5个方块后换一行
        }
        k++;
    }
    printf("\n");
}
int mgpath(int xi,int yi,int xe,int ye)                 //搜索路径为:(xi,yi)->(xe,ye)
{
    int i,j,find=0,di;
    QuType qu;                      //定义顺序队
    qu.front=qu.rear=-1;
    qu.rear++;
    qu.data[qu.rear].i=xi;
    qu.data[qu.rear].j=yi;  //(xi,yi)进队
    qu.data[qu.rear].pre=-1;
    mg[xi][yi]=-1;                  //将其赋值-1,以避免回过来重复搜索
    while (qu.front!=qu.rear && !find)  //队列不为空且未找到路径时循环
    {
        qu.front++;                 //出队,由于不是环形队列，该出队元素仍在队列中
        i=qu.data[qu.front].i;
        j=qu.data[qu.front].j;
        if (i==xe && j==ye)         //找到了出口,输出路径
        {
            find=1;
            print(qu,qu.front);         //调用print函数输出路径
            return(1);              //找到一条路径时返回1
        }
        for (di=0; di<4; di++)      //循环扫描每个方位,把每个可走的方块插入队列中
        {
            switch(di)
            {
            case 0:
                i=qu.data[qu.front].i-1;
                j=qu.data[qu.front].j;
                break;
            case 1:
                i=qu.data[qu.front].i;
                j=qu.data[qu.front].j+1;
                break;
            case 2:
                i=qu.data[qu.front].i+1;
                j=qu.data[qu.front].j;
                break;
            case 3:
                i=qu.data[qu.front].i, j=qu.data[qu.front].j-1;
                break;
            }
            if (mg[i][j]==0)
            {
                qu.rear++;              //将该相邻方块插入到队列中
                qu.data[qu.rear].i=i;
                qu.data[qu.rear].j=j;
                qu.data[qu.rear].pre=qu.front; //指向路径中上一个方块的下标
                mg[i][j]=-1;        //将其赋值-1,以避免回过来重复搜索
            }
        }
    }
    return(0);                      //未找到一条路径时返回1
}
int main()
{
    mgpath(1,1,M,N);
    return 0;
}